
Визначений інтеграл.
Визначений інтеграл
![]() при
при
![]() чисельно дорівнює площі
чисельно дорівнює площі
![]() криволінійної трапеції, утвореної
кривою
криволінійної трапеції, утвореної
кривою
![]() ,
віссю ОХ і відрізками прямих
,
віссю ОХ і відрізками прямих
![]() .
.
Формула Ньютона-Лейбніца.
Якщо функція
![]() визначена і неперервна на відрізку
визначена і неперервна на відрізку
![]() ,
а
,
а
![]() -
її первісна, то
-
її первісна, то
![]()
Формула інтегрування частинами.
Якщо існують
![]() - неперервно-диференційовні функції на
- неперервно-диференційовні функції на
![]() ,
то
,
то
![]() .
.
Формула заміни змінних.
Якщо
![]() неперервна на відрізку
неперервна на відрізку
![]() функція, а
функція, а
![]() - неперервно-диференційовні функції на
- неперервно-диференційовні функції на
![]() ,
де
,
де
![]() ,
,
![]() ,
то
,
то
![]()
Завдання 17. Обчислити дані інтеграли.
1.![]() 2.
2.![]()
3.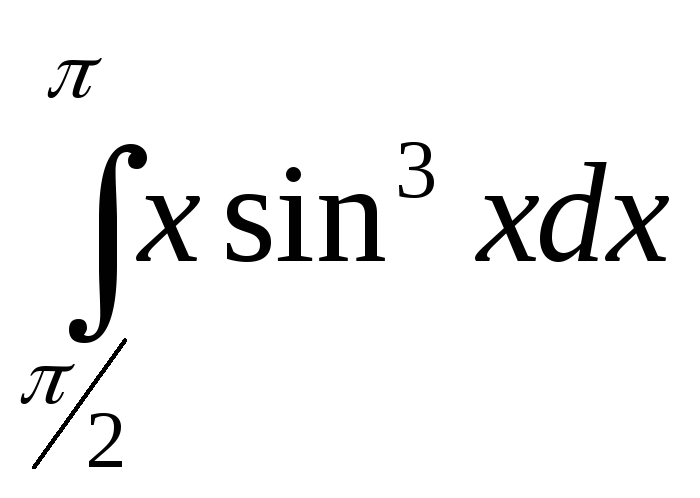 4.
4.
5. 6.
6.![]()
7.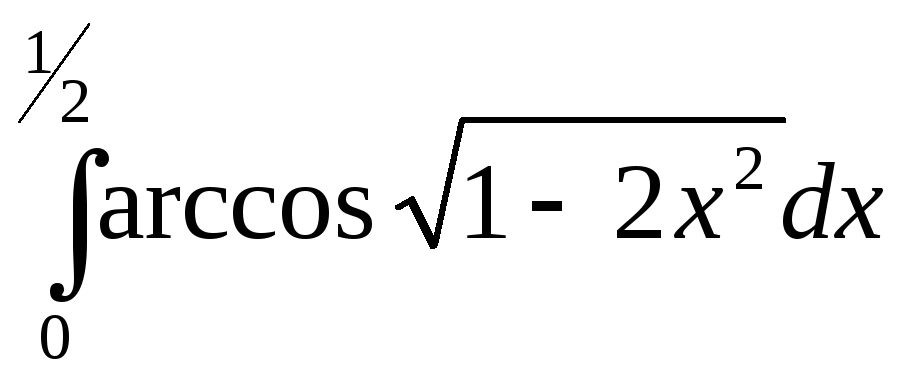 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.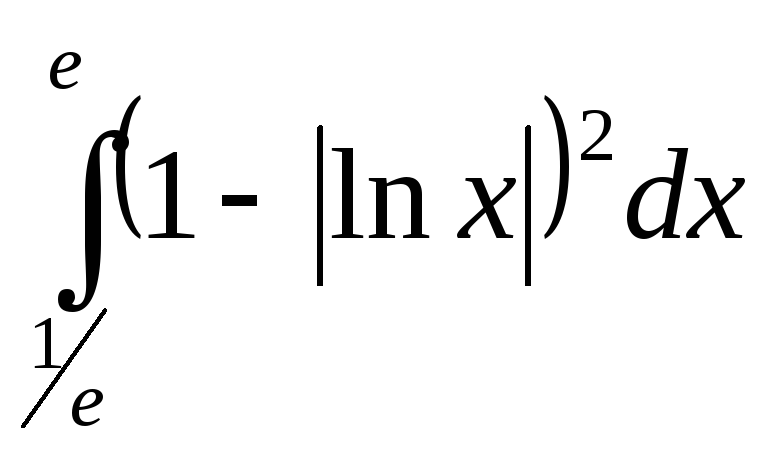 14.
14.![]()
15.![]() 16.
16.![]()
17. 18.
18.![]()
19.![]() 20.
20.![]()
21. 22.
22.
23. 24.
24.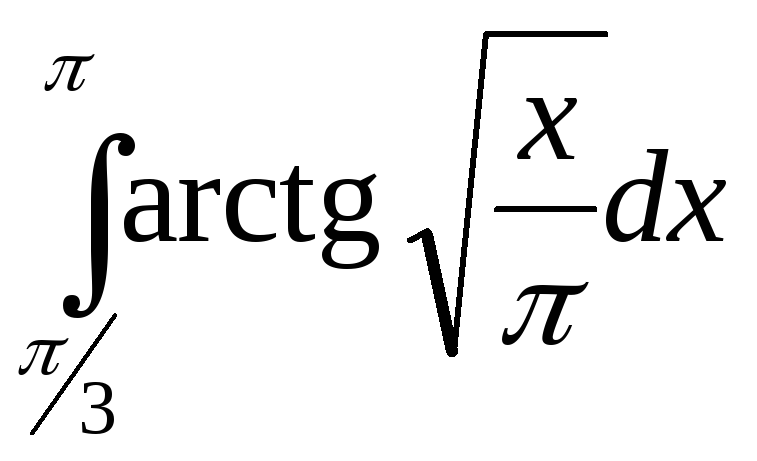
25.![]()
Завдання 18. Обчислити площу фігури, обмеженої заданими полярними кривими.
1.![]()
2.
![]() 3.
3.![]() (1
пелюстка)
(1
пелюстка)
4.
![]() 5.
5.![]() (1
пелюстка)
(1
пелюстка)
6.
![]() 7.
7.![]()
8.
![]() 9.
9.![]()
10.![]()
11.![]()
12.![]()
13.![]()
14.![]()
15.![]()
16.
![]() 17.
17.![]()
18.
![]() 19.
19.![]()
20.
![]() 21.
21.![]()
22.
![]() 23.
23.![]()
24.
![]() 25.
25.![]()
Числові ряди.
Числовий ряд
(1)
![]()
називається
збіжним, якщо існує скінченна границя:![]() ,
де
,
де
![]() .
У супротивному разі ряд (1) називається
розбіжним.
.
У супротивному разі ряд (1) називається
розбіжним.
Якщо ряд (1) – збіжний, то послідовність його членів є нескінченно малою:
![]() (необхідна умова
збіжності ряду).
(необхідна умова
збіжності ряду).
Якщо
![]() ,то
ряд (1) - розбіжний (груба ознака
розбіжності).
,то
ряд (1) - розбіжний (груба ознака
розбіжності).
Ряд (1) називаєтьс абсолютно збіжним, якщо збігається ряд
(2)
![]() .
.
В цьому разі ряд (1) також збігається . Якщо ряд (1) збігається, а ряд (2) розбігається, то ряд (1) називається умовно збіжним.
Ознаки збіжності числових рядів.
Перша ознака порівняння. Розглянемо також ряд
(3)
![]()
Якщо
![]() ,
то із збіжності ряду (3) випливає збіжність
ряду (1). Із розбіжності ряду (1) випливає
розбіжність ряду (3).
,
то із збіжності ряду (3) випливає збіжність
ряду (1). Із розбіжності ряду (1) випливає
розбіжність ряду (3).
Друга ознака
порівняння. Якщо
![]() ,
то ряд (1) збігається при
,
то ряд (1) збігається при
![]() і розбігається при
і розбігається при
![]() .
.
Ознака Даламбера.
Якщо
![]() і
і
![]() ,
то ряд (1) збігається при
,
то ряд (1) збігається при
![]() і розбігається при
і розбігається при
![]() .
.
Ознака Коші.
Якщо
![]() і
і
![]() ,
то ряд (1) збігається при
,
то ряд (1) збігається при
![]() і розбігається при
і розбігається при
![]() .
.
Ознака Раабе.
Якщо
![]() і
і
![]() ,
то ряд (1) збігається при
,
то ряд (1) збігається при
![]() і розбігається при
і розбігається при
![]() .
.
Ознака Лейбніца збіжності знакозмінного ряду.
Ряд
![]() ,
де
,
де
![]() збігається , якщо 1)
збігається , якщо 1)![]() і 2)
і 2)
![]() .
.
Завдання 19. Дослідити збіжність числового ряду.
1.![]() 2.
2.![]()
3. 4.
4.![]()
5.![]() 6.
6.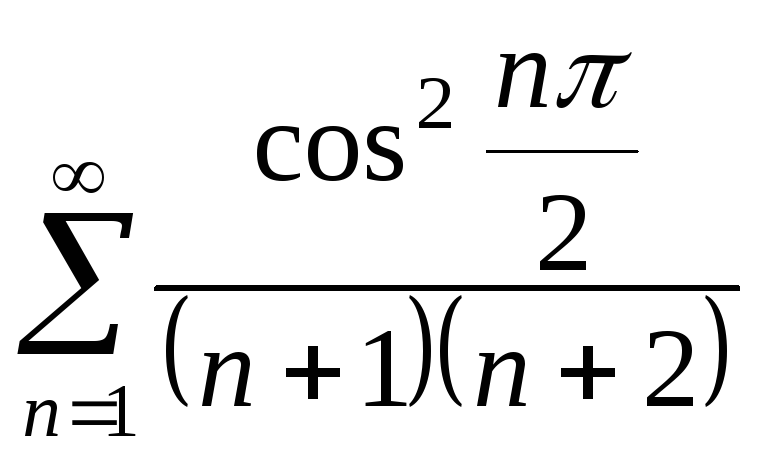
7. 8.
8.![]()
9. 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.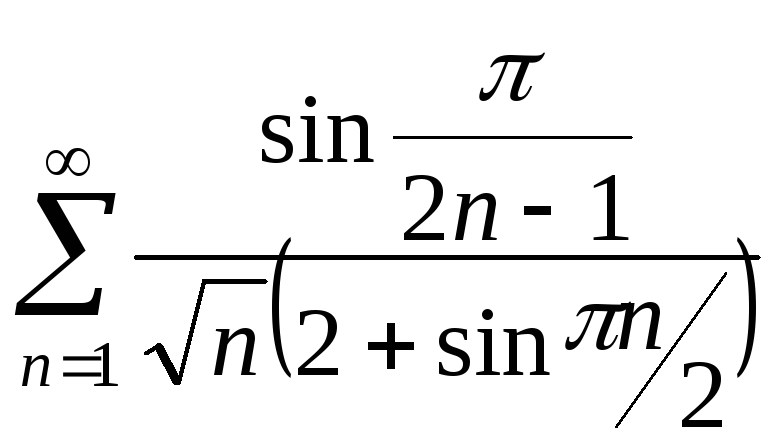
19.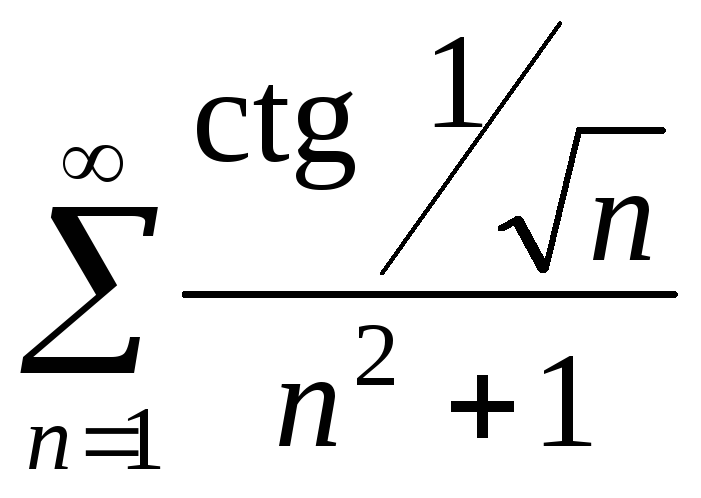 20.
20.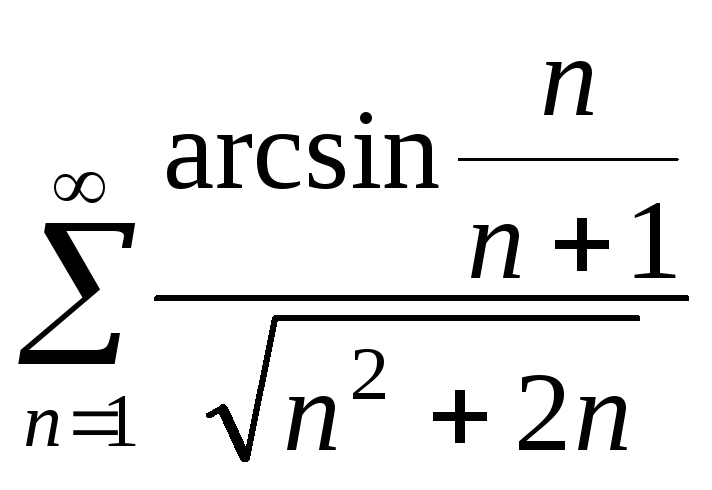
21.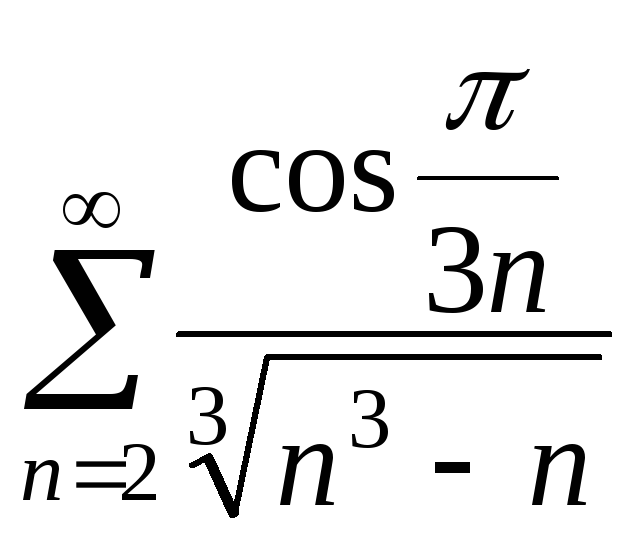 22.
22.![]()
23. 24.
24.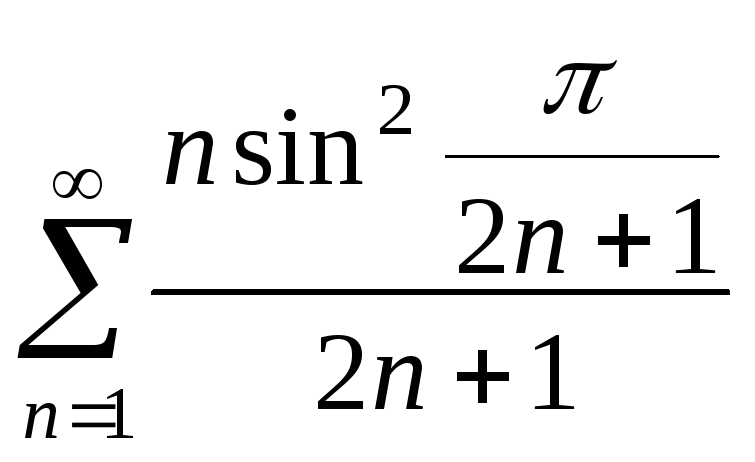
25.
Завдання 20. Дослідити збіжність ряду.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19. 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.![]()
25.![]()
Завдання 21. Дослідити збіжність ряду.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.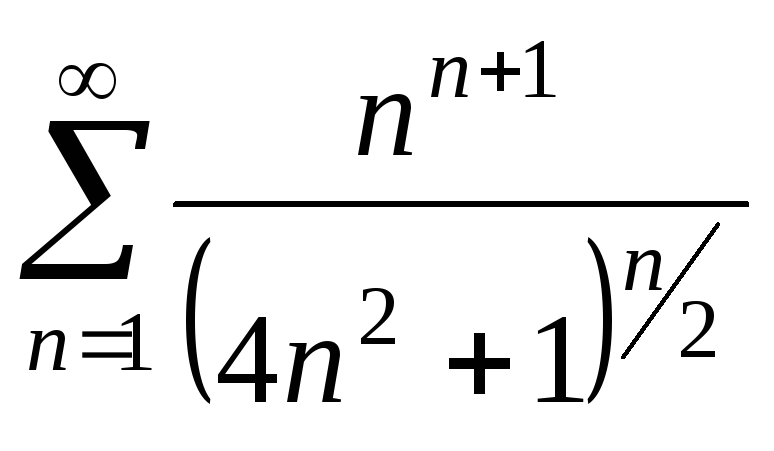
13.![]() 14.
14.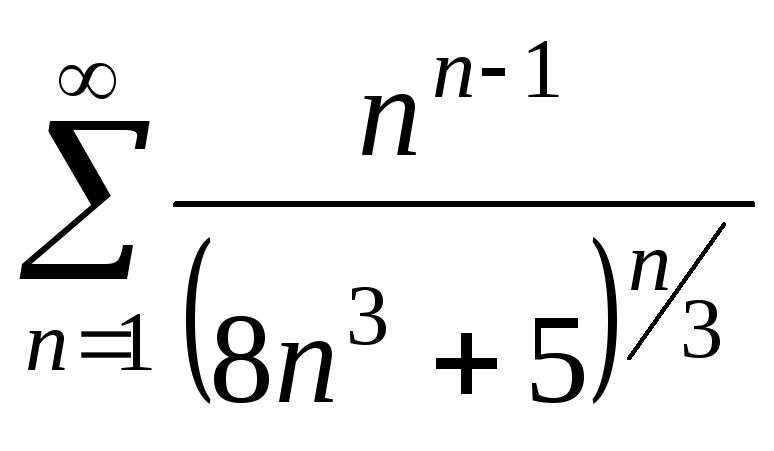
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.![]()
25.![]()
Завдання 22. Дослідити збіжність знакозмінного ряду.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19. 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.![]()
25.![]()
Функціональні ряди.
Сукупність
![]() усіх значень
усіх значень
![]() ,
при яких збігається ряд
,
при яких збігається ряд
(1)
![]() ,
,
де
![]() - деякі дійсні функції, називається
областю збіжності
- деякі дійсні функції, називається
областю збіжності
функціонального
ряду (1), а функція
![]()
називається сумою ряду (1).
Рівномірна збіжність.
Послідовність
функцій
![]() рівномірно збігається на множині
рівномірно збігається на множині
![]() ,
якщо :
,
якщо :
існує гранична
функція
![]() ;
;
![]() .
.
Рівномірна збіжність
позначається як
![]() .
.
Наведене означення рівномірної збіжності послідовності функцій еквівалентне виконанню граничної рівності:
![]() .
.
Функціональний
ряд (1) називається рівномірно збіжним
на множині
![]() ,
якщо послідовність його частинних сум
,
якщо послідовність його частинних сум
![]() рівномірно збігається на множині
рівномірно збігається на множині
![]()
![]() .
.
Ознака Вейерштрасса рівномірної збіжності функціонального ряду.
Ряд (1) збігається
абсолютно і рівномірно на множині
![]() ,
якщо існує збіжний числовий ряд
,
якщо існує збіжний числовий ряд
![]() такий,
що
такий,
що
![]() ,
,
![]()
Степеневі ряди..
Функціональний
ряд (1) у якого
![]() називається степеневим рядом за степенями
називається степеневим рядом за степенями
![]() .
Для кожного степеневого ряду існує
інтервал збіжності
.
Для кожного степеневого ряду існує
інтервал збіжності
![]() ,
всередині якого степеневий ряд збігається
, а зовні – розбігається. Радіус збіжності
,
всередині якого степеневий ряд збігається
, а зовні – розбігається. Радіус збіжності
![]() визначається
по формулі Коші-Адамара:
визначається
по формулі Коші-Адамара:
![]() , або
, або
![]() .
.
Ряд Тейлора.
Функція
![]() ,
яка має достатню кількість похідних в
точці
,
яка має достатню кількість похідних в
точці
![]() може бути записана у вигляді степеневий
ряд за степенями
може бути записана у вигляді степеневий
ряд за степенями
![]() :
:
![]() .
.
Залишковий член
цього ряду
![]() може бути поданий у формі Пєано:
може бути поданий у формі Пєано:
![]() ,
або у формі Лагранжа :
,
або у формі Лагранжа :
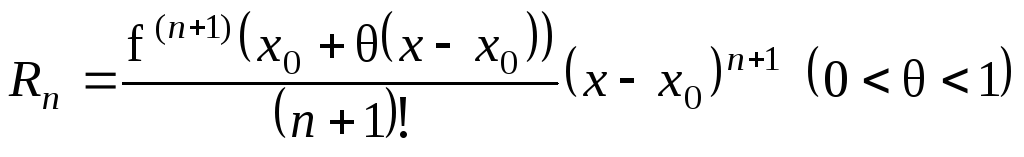
Ряди Фур’є.
Якщо 1) функція
![]() визначена на інтервалі
визначена на інтервалі
![]() ,
періодична з періодом
,
періодична з періодом
![]() ,
є кусково-гладкою на вказанному інтервалі,
то у кожній точці
,
є кусково-гладкою на вказанному інтервалі,
то у кожній точці
![]() неперервності функції
неперервності функції
![]() має місце рівність :
має місце рівність :
(2)
![]() , де
, де
![]()
![]() ,
,
![]()
Ряд (2) називається
тригонометричним рядом Фур’є
періодичної функції
![]() .
Якщо
.
Якщо
![]() - точка розриву функції
- точка розриву функції
![]() ,
то тригонометричний ряд Фур’є
збігається у цій точці до значення
,
то тригонометричний ряд Фур’є
збігається у цій точці до значення
![]() .
.
Завдання 23. Знайти області збіжності (абсолютної та умовної) функціонального ряду.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.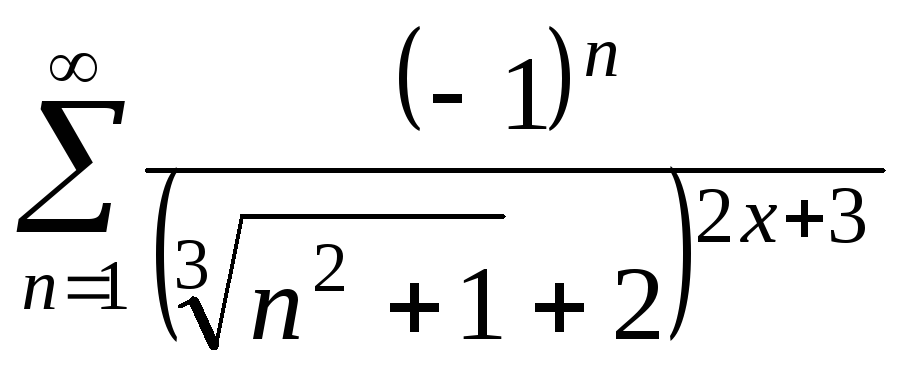
25.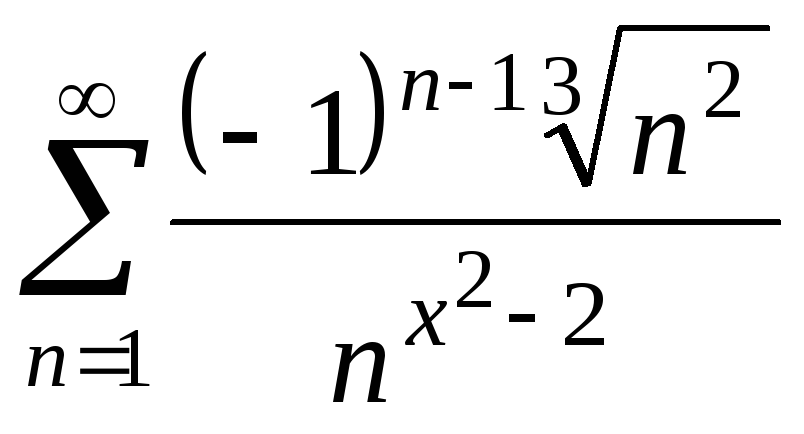
Завдання 24. Знайти області збіжності (абсолютної та умовної) функціонального ряду.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7. 8.
8.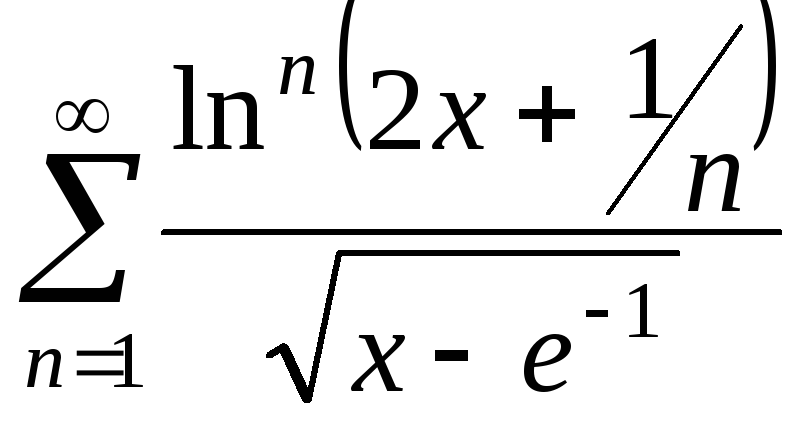
9.![]() 10.
10.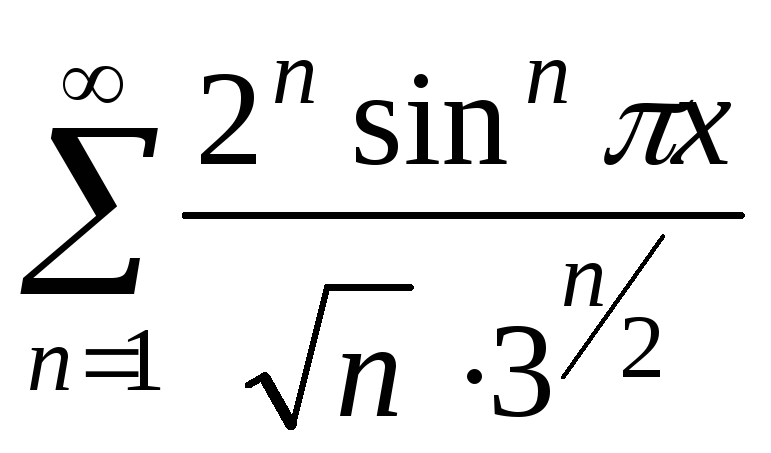
11.![]() 12.
12.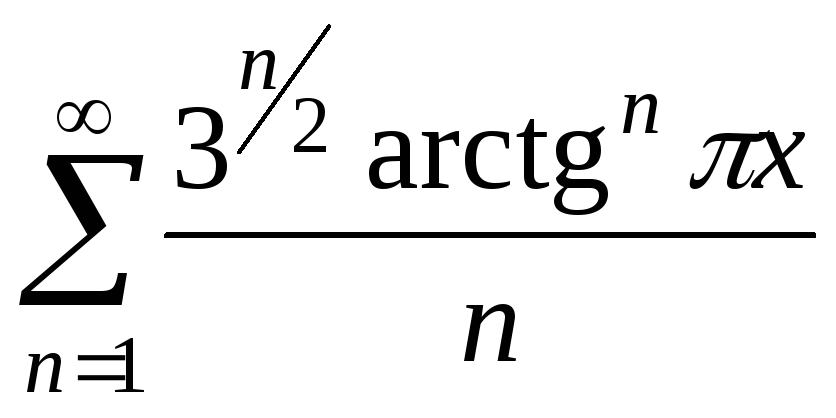
13.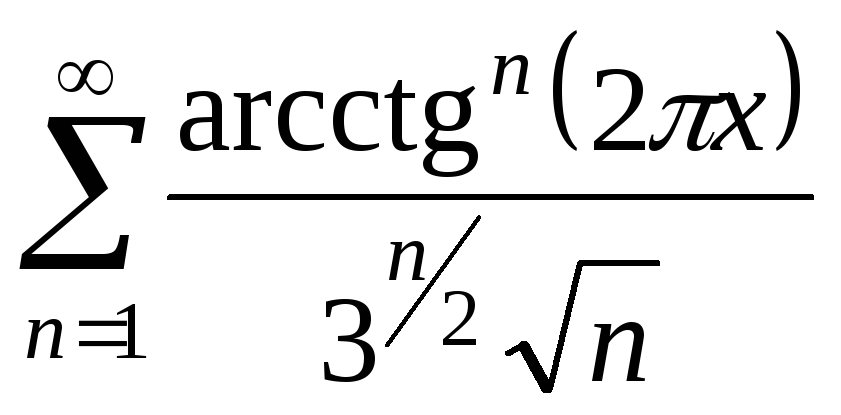 14.
14.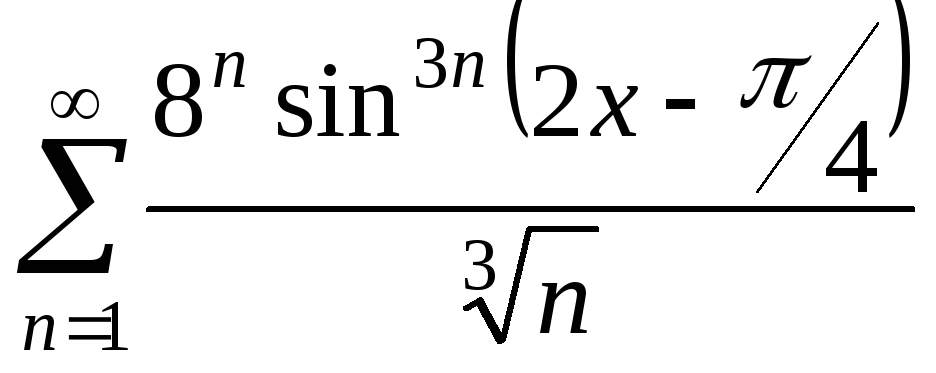
15. 16.
16.
17. 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.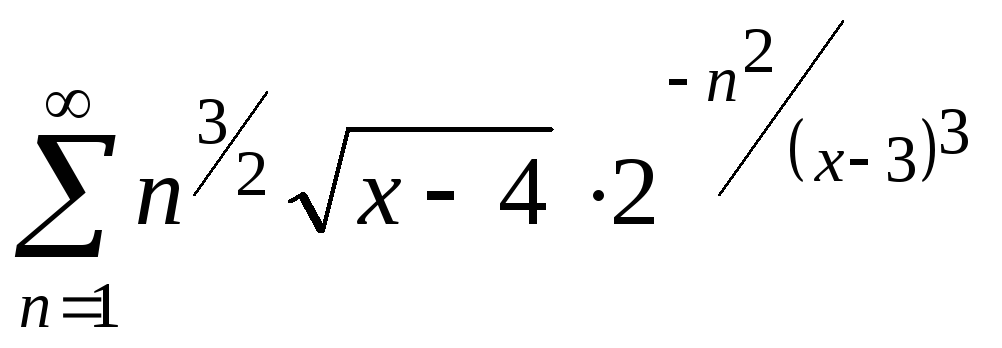
23.![]() 24.
24.![]()
25.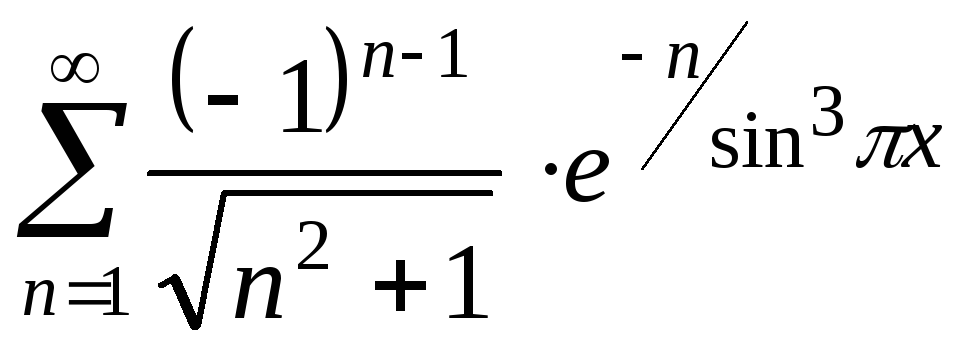
Завдання 25. Визначити радіус та інтервал збіжності степеневого ряду та дослідити його поведінку в граничних точках інтервалу збіжності.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.![]()
25.![]()
Завдання 26.
Розкласти функцію
![]() в ряд Тейлора.
в ряд Тейлора.
1.![]() по степенях
по степенях
![]() .
.
2.![]() по степенях
по степенях
![]() .
.
3.![]() по степенях
по степенях
![]() .
.
4.![]() по степенях
по степенях
![]() .
.
5.![]() по степенях
по степенях
![]() .
.
6.![]() по степенях
по степенях
![]() .
.
7.![]() по степенях
по степенях
![]() .
.
8.![]() по степенях
по степенях
![]() .
.
9.![]() по степенях
по степенях
![]() .
.
10.![]() по степенях
по степенях
![]() .
.
11.![]() по степенях
по степенях
![]() .
.
12.![]() по степенях
по степенях
![]() .
.
13.![]() по степенях
по степенях
![]() .
.
14.![]() по степенях
по степенях
![]() .
.
15.![]() по степенях
по степенях
![]() .
.
16.![]() по степенях
по степенях
![]() .
.
17.![]() по степенях
по степенях
![]() .
.
18.![]() по степенях
по степенях
![]() .
.
19.![]() по степенях
по степенях
![]() .
.
20.![]() по степенях
по степенях
![]() .
.
21.![]() по степенях
по степенях
![]() .
.
22.![]() по степенях
по степенях
![]() .
.
23.![]() по степенях
по степенях
![]() .
.
24.![]() по степенях
по степенях
![]() .
.
25.![]() по степенях
по степенях
![]() .
.
Завдання 27. Розкласти функцію в ряд Фур’є на вказанному проміжку.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.![]()
23.![]() 24.
24.![]()
25.![]()
