
матан 3 курс 2013 / практика / Невласні інтеграли / практическое занятие № 11
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ПРАКТИЧНЕ ЗАНЯТТЯ № 11
з теми: «Дослідження інтегралів на збіжність.»
Модуль КЗН-02. ПР.О.03.09 Невласні інтеграли
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики
протокол № ____ від _______20__ р.
Голова циклової комісії ПМ О.В. Велікодна
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІI
Викладач: Велікодна Ольга Володимирівна.
Тема: Дослідження інтегралів на збіжність.
Мета:
-
Дидактична: виробити вміння досліджувати на збіжність невласні інтеграли, використовуючи визначення чи відповідні ознаки збіжності.
-
Виховна: підвищити рівень засвоєння навчального матеріалу, розвивати наукове мислення, усне мовлення студентів.
-
Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.
Тип: практичне заняття
Вид: практичне заняття – дослідження.
Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.
Наочні посібники: -
Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.
Обчислювальні засоби: -
Література:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
ХІД ЗАНЯТТЯ
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Мотивація навчальної діяльності студентів: вивчити основний математичний апарат –інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.
-
Актуалізація опорних знань: визначення невласних інтегралів, ознаки збіжності невласних інтегралів від додатних функцій.
-
Контроль за підготовкою студентів до практичного заняття:
-
Інструктаж щодо виконання практичної роботи.
-
Видача завдань для виконання роботи.
-
Виконання студентами практичної роботи.
-
Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.
-
Підведення підсумків. Оцінювання.
-
Домашнє завдання:
Конспект практичного заняття № 11.
Тема: «Дослідження інтегралів на збіжність.»
Методичні вказівки.
Нехай функція ƒ визначена на
скінченому чи нескінченому полу інтервалі
[a, b), - ∞ < a < b ≤ + ∞, та для будь – якого
числа ε
![]() [a,
b), інтегрована на відрізку [a, ε].
[a,
b), інтегрована на відрізку [a, ε].
Функція
![]() верхньої границі інтегрування, a ≤ ε
< b, називається невласним
інтегралом та позначається
верхньої границі інтегрування, a ≤ ε
< b, називається невласним
інтегралом та позначається
![]() .
Якщо існує скінчена границя
.
Якщо існує скінчена границя
![]() ,
то невласний інтеграл
,
то невласний інтеграл
![]() називається збіжним,
а якщо ця границя нескінчена чи не існує,
то – розбіжним.
називається збіжним,
а якщо ця границя нескінчена чи не існує,
то – розбіжним.
Тобто маємо:
![]() =
=
![]() .
Можливі два випадки: коли b – скінчене
число та коли b – нескінчене число.
.
Можливі два випадки: коли b – скінчене
число та коли b – нескінчене число.
Якщо існує скінчена границя
![]() ,
то невласний інтеграл
,
то невласний інтеграл
![]() називається збіжним,
а якщо ця границя нескінчена чи не існує,
то – розбіжним.
називається збіжним,
а якщо ця границя нескінчена чи не існує,
то – розбіжним.
Тобто маємо:
![]() =
=
![]() .
.
Якщо функція ƒ неперервна
на проміжку [a, b), та Φ – деяка її первісна,
то
![]() = Φ(b-0) – Φ(а).
= Φ(b-0) – Φ(а).
Ознаки збіжності для невласних інтегралів від невід’ємних функцій.
Теорема.(ознака
зрівняння) Нехай 0 ≤ g(х) ≤ ƒ(х), х
![]() [a,
b). Тоді: 1) якщо
[a,
b). Тоді: 1) якщо
![]() збігається, то збігається й інтеграл
збігається, то збігається й інтеграл
![]() ;
2) якщо інтеграл
;
2) якщо інтеграл
![]() розбігається, то розбігається й інтеграл
розбігається, то розбігається й інтеграл
![]() .
.
Наслідки.
Нехай функції g(х) та ƒ(х) невід’ємні
на полу інтервалі [а, b), g(х) ≠ 0 при всіх
х
![]() [a,
b) та існує скінчена чи нескінчена границя
[a,
b) та існує скінчена чи нескінчена границя
![]() .
Тоді:
.
Тоді:
-
якщо інтеграл
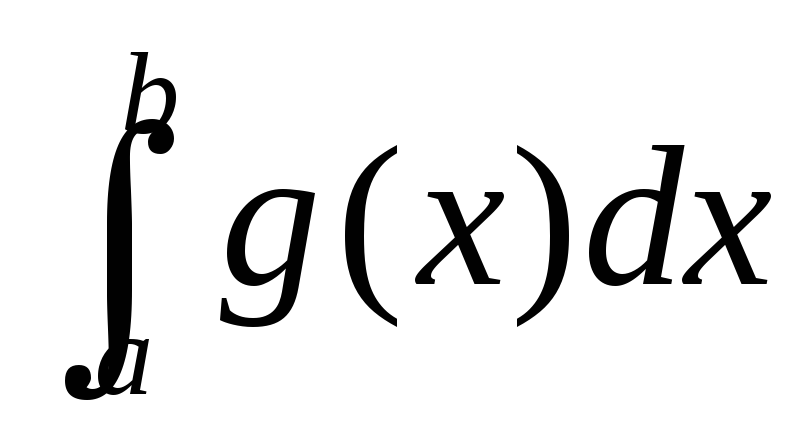 збігається та 0 ≤ k < +∞, то й інтеграл
збігається та 0 ≤ k < +∞, то й інтеграл
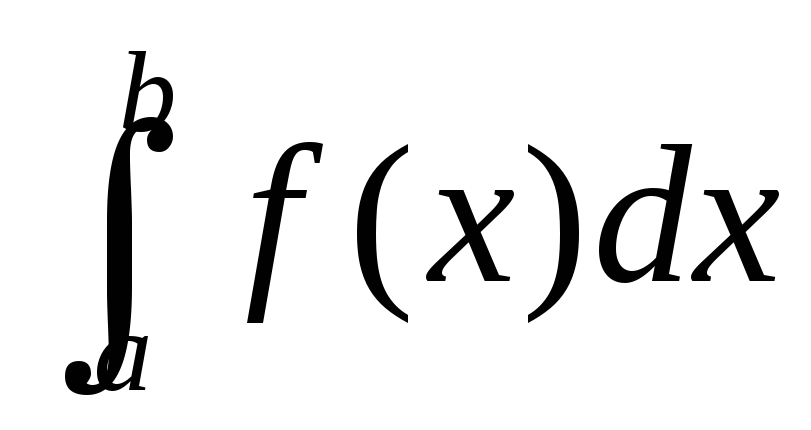 збігається;
збігається; -
якщо інтеграл
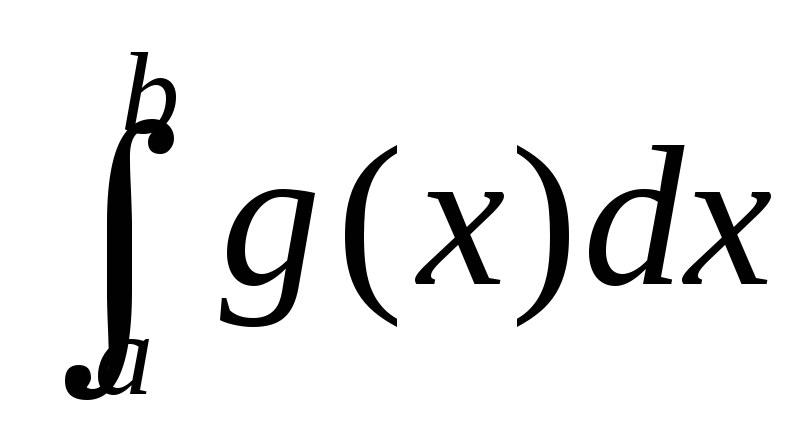 розбігається та 0 < k ≤ +∞, то й інтеграл
розбігається та 0 < k ≤ +∞, то й інтеграл
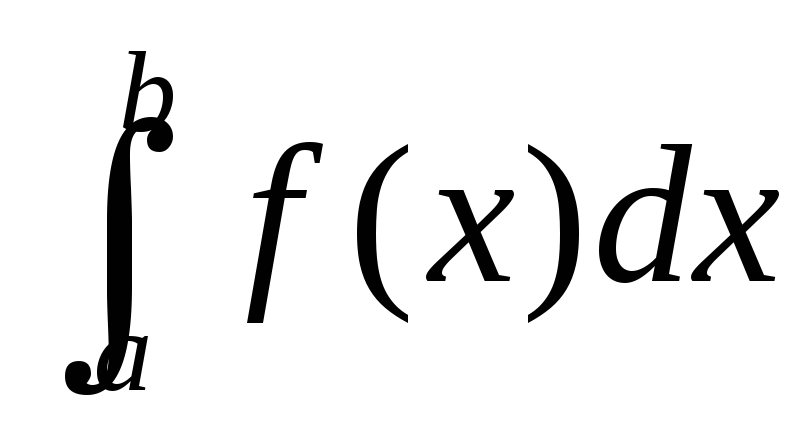 розбігається.
розбігається.
Зокрема, якщо
![]() ,
то інтеграли
,
то інтеграли
![]() та
та
![]() одночасно збігаються та розбігаються.
одночасно збігаються та розбігаються.
Теорема.(критерій
Коші збіжності інтегралів) Невласний
інтеграл
![]() збігається тоді та тільки тоді, коли
збігається тоді та тільки тоді, коли
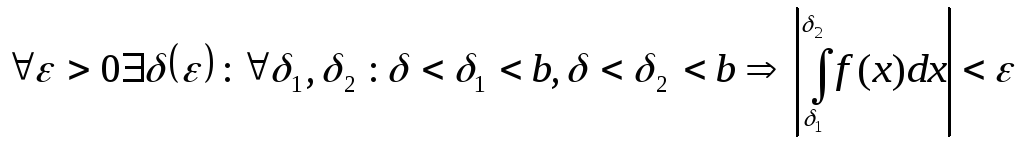 .
.
Нехай функція ƒ визначена на
скінченому чи нескінченому полуінтервалі
[a, b), - ∞ < a < b ≤ + ∞, та для будь – якого
числа ε
![]() [a,
b), інтегрована за Ріманом на відрізку
[a, ε].
[a,
b), інтегрована за Ріманом на відрізку
[a, ε].
Невласний інтеграл
![]() називається абсолютно збіжним, якщо
збігається інтеграл
називається абсолютно збіжним, якщо
збігається інтеграл
![]() .
.
Теорема.(критерій
Коші абсолютної збіжності інтеграла)
Для того, щоб невласний інтеграл
![]() абсолютно збігаєшся, необхідно та
достатньо, щоб
абсолютно збігаєшся, необхідно та
достатньо, щоб
 .
.
Теорема. Якщо невласний інтеграл абсолютно збігається, то він і просто збігається. (зворотне твердження не вірне).
Достатні умови збіжності невласних інтегралів:
Теорема.(ознака Дирихлє) Якщо на полуосі х ≥ а:
1) функція ƒ неперервна та має обмежену первісну,
2) функція g неперервно
диференційована та спадає, рухаючись
до 0 при х → +∞, то інтеграл
![]() збігається.
збігається.
Теорема.(ознака Абеля) Якщо на полуосі х ≥ а:
1) функція ƒ неперервна
та інтеграл
![]() збігається,
збігається,
2) функція g неперервно
диференційована, обмежена та монотонна,
то інтеграл
![]() збігається.
збігається.
Інструктаж до виконання практичних завдань.
Приклади виконання практичних завдань.
Приклад 1. Обчислити інтеграл чи встановити його розбіжність.

Розв’язання:
-
Підінтегральна функція необмежена в будь – якому околі точки х=1 та інтегрована на будь – якому відрізку
 ,
,
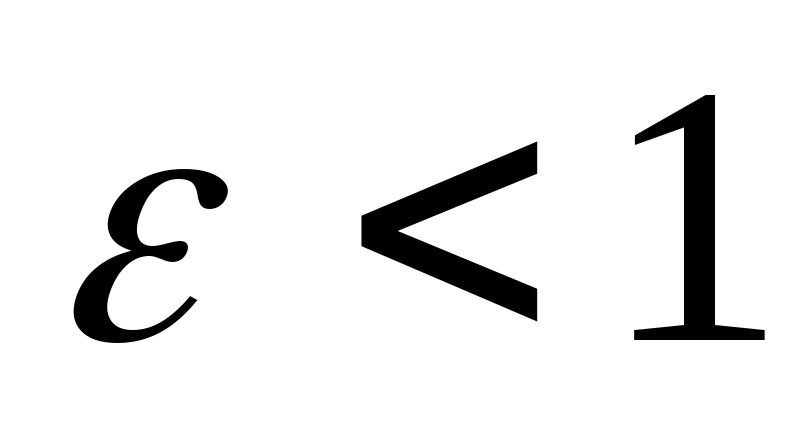 .
За визначенням невласного інтегралу
маємо:
.
За визначенням невласного інтегралу
маємо:
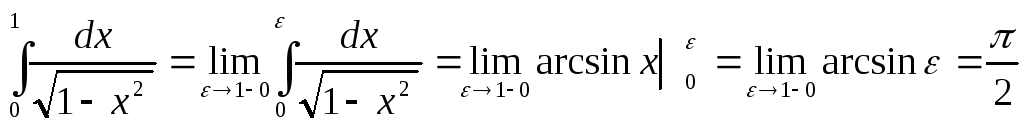 .
. -
Підінтегральна функція необмежена в правому околі точки х=0, тому

-
Підінтегральна функція необмежена в околі точки х = 0. даний інтеграл збігається, якщо збігається кожен з інтегралів
 .
Але перший з інтегралів розбігається,
так як
.
Але перший з інтегралів розбігається,
так як
 .
.
Приклад
2.
Дослідити інтеграл
![]() на збіжність.
на збіжність.
Розв’язання: нехай α ≠ 1. Тоді :
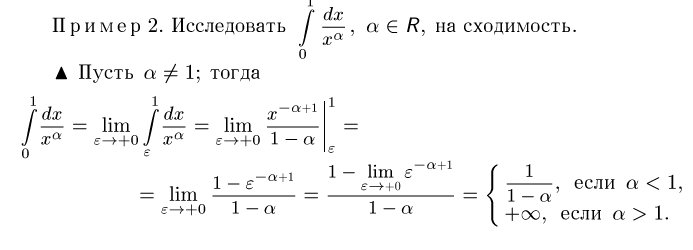
Нехай α = 1. Тоді:

Відповідно,
інтеграл
![]() збігається при
збігається при
![]() ,
та розбігається при
,
та розбігається при
![]() .
.
Приклад
3.
Обчислити інтеграл
![]() .
.
Розв’язання:
введемо заміну змінної в невласному
інтегралі. Нехай
![]() .
Нові границі інтегрування
.
Нові границі інтегрування
![]() .
.
Отже маємо:

Приклад
4.
Обчислити інтеграл
![]() .
.
Розв’язання: застосовуємо формулу інтегрування за частинами.
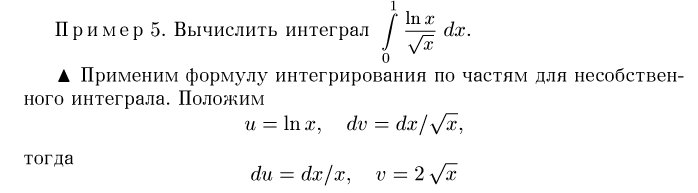
Відповідно маємо:
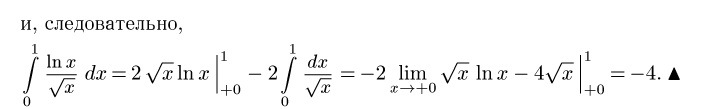
Практичні завдання для студентів.
-
Обчислити інтеграл чи встановити його розбіжність.


-
Дослідити на збіжність інтеграли:

