матан 3 курс 2013 / лекции / Частинні похідні і диференціали / лекция № 33

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 33

з теми: «Геометричний зміст частинних похідних та диференціалу. Похідна за напрямом. Градієнт.»

Модуль КЗН-02.ПР.О.03.13 Частинні похідні і диференціали

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Геометричний зміст частинних похідних та диференціалу. Похідна за напрямом. Градієнт.

Мета:

• Дидактична: вивчити геометричний зміст частинних похідних функції багатьох змінних, розглянути практичне застосування геометричного змісту, вивчити поняття похідної за напрямом та градієнту функції багатьох змінних.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики проектної технології.

Тип: лекція

Вид: лекція з використанням проектної технології.

Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: диференційованість функції двох змінної, визначення частинних похідних та диференціала функції двох змінної, таблиця похідних основних елементарних функцій, правила обчислення похідних функцій однієї змінної, похідна складної функції двох змінних. Інваріантність форми першого диференціалу.

3. Вивчення нового матеріалу:

• Тема лекції: Геометричний зміст частинних похідних та диференціалу. Похідна за напрямом. Градієнт.

• Мотивація вивчення матеріалу: вивчити основні методи дослідження функцій багатьох змінних для подальшого їх застосування як при розв’язанні математичних, так і прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 33.

Тема: Геометричний зміст частинних похідних та диференціалу. Похідна за напрямом. Градієнт.

План лекції № 33.

1. Геометричний зміст частинних похідних та диференціалу.

2. Похідна за напрямом. Градієнт.

Розглянемо функцію двох змінних z = ƒ(х, у). Нехай в точці функція має частинну похідну , де α за геометричним змістом похідної функції однієї змінної є кутом нахилу дотичної до графіку цієї функції, тобто до кривої z = ƒ(х, у), у = у0, в точці (х0, у0, z0), де z0 = ƒ(х0, у0). В цьому й є зміст частинної похідної.

Далі, диференційованість функції z = ƒ(х, у) в точці (х0, у0) означає, що .

Підставимо відповідні вирази у рівність та отримаємо .

Площина, що визначається рівнянням називається дотичною площиною до графіку функції z = ƒ(х, у) в точці (х0, у0, z0). Якщо аплікату дотикання позначити z0, то , z = ƒ(х, у). Також, . Таким чином, диференціал функції дорівнює приросту аплікати дотичної площини до графіку функції.

Нехай функція диференційовна в точці деякої області. Перетнемо поверхню , що зображає функцію , площинами і Площина перетинає поверхню по деякій лінії , рівняння якої виходить підстановкою у вираз початкової функції замість числа . Точка належить кривій. Через диференційовність функції в точці функція також диференціюється в точці . Тому, в цій точці площини до кривої може бути проведена дотична пряма .

Проводячи аналогічні міркування для перетину , побудуємо дотичну пряму до кривої в точці . Прямі і визначають площину, яка називається дотичною площиною до поверхні в точці .

Складемо її рівняння. Оскільки площина проходить через точку , то її рівняння може бути записано у вигляді

яке можна переписати так:

(розділивши рівняння на і позначивши ).

Знайдемо і : Рівняння дотичних і мають вигляд

відповідно.

Дотична лежить в площині , отже, координати всіх точок задовольняють рівняння (3.1). Цей факт можна записати у вигляді системи

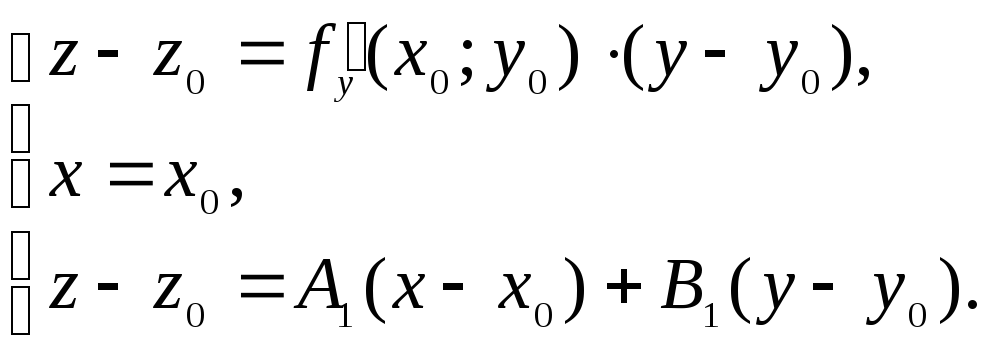
Розв’язуючи цю систему відносно , отримаємо, що Проводячи аналогічні міркування для дотичної , легко встановити, що

Підставивши значення і в рівняння (3.1), одержуємо шукане рівняння дотичної площини:

Пряма, що проходить через точку і перпендикулярна дотичній площини, побудованої в цій точці поверхні, називається її нормаллю.

Використовуючи умову перпендикулярності прямої і площини, легко отримати канонічні рівняння нормалі:

Якщо поверхня задана рівнянням , то

і

Зауваження. Формули дотичної площини і нормалі до поверхні отримані для звичайних, тобто не особливих, точок поверхні. Точка поверхні називається особливою, якщо в цій точці всі частинні похідні рівні нулю або хоча б одна з них не існує. Такі точки ми не розглядаємо.

Приклад. А) Написати рівняння дотичної площини і нормалі до параболоїда обертання в точці .

Тут, , ,

Користуючись формулами (3.2) і (3.3) одержуємо рівняння дотичної площини:

або і рівняння нормалі:

Б) Скласти рівняння дотичної площини і нормалі до поверхні у точці :

а) у точці .

Знайдемо : . Отже, .

Позначимо .Тоді частинні похідні:

, , .

Обчислимо значення частинних похідних в точці :

,

,

.

Згідно з формулою (2.9), рівняння дотичної площини має вигляд:

,

або .

За формулою (2.10) складемо рівняння нормалі:

.

б) у точці .

Знайдемо , , .

Значення частинних похідних в точці :

,

,

.

Складемо рівняння дотичної площини:

,

або .

Рівняння нормалі:

або .

Нехай функція ƒ(х, у, z) визначено в околі точки (х0, у0, z0) та заданий вектор l, l ≠ 0. Позначимо через його напрямні косинуси, тобто координати одиничного вектору . Проведемо через точку (х0, у0, z0) луч в напрямку вектору l та запишемо рівняння в параметричному вигляді: , де t – відстань від точки (х, у, z) луча, що відповідає значенню параметру t до точки (х0, у0, z0).Розглянемо композицію функцій ƒ(х, у, z) та , тобто . Права похідна цієї функції в точці t=0 називається похідною функції ƒ(х, у, z) в точці (х0, у0, z0) за напрямом вектору l, та позначається .

=. Якщо М0=(х0, у0, z0), М=(х, у, z) – точки луча, то М0М =t, та . Всі величини в правій частині рівності не залежать від вибору системи координат, тому й похідна за напрямом в точці М0 не залежить від вибору системи координат. Функції лінійні відносно t, тому диференційовані. Тоді, похідна складної функції по змінній t буде дорівнювати похідній функції . Користуючись формулою диференціювання складної функції, отримаємо , де . Далі будемо мати: - похідна функції ƒ(х, у, z) в точці (х0, у0, z0) за напрямом вектору l.

Вектор називається градієнтом функції ƒ(х, у, z) та позначається . Градієнт функції не залежить від вибору системи координат, якщо , то напрямок градієнту є єдиним напрямом, за яким похідна за напрямом в даній точці має найбільше значення, а довжина градієнту дорівнює цьому найбільшому значенню. Якщо ж , то в даній точці похідні за всіма напрямами дорівнюють нулю.

Приклади.