Дисперсия случайной величины

Определение 11. Дисперсией случайной величины  называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

 (18)

Если  - дискретная случайная величина, принимающая конечное число значений, то

 (19)

Если  - дискретная случайная величина, принимающая бесконечное , но счетное число значений, то

 (20)

Если  - непрерывная случайная величина, принимающая значения на конечном промежутке , то

 (21)

Если  - непрерывная случайная величина, принимающая значения на всей числовой оси, то

 (22)

Дисперсия для дискретной случайной величины, принимающей бесконечное, но счетное число значений,  существует, если ряд (20) сходится, а для непрерывной случайной величины, принимающейзначения на всей  числовой оси, если интеграл (22) сходится.

Свойства дисперсии.

1. Дисперсия константы равна нулю: ; 2. ; 3. Если и - независимые случайные величины, то ; 4. Если и - независимые случайные величины, то . Дисперсию иногда удобнее вычислять по формуле:

 (23)

Если  - дискретная случайная величина с конечным числом значений, то

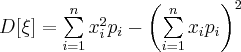 (24)

Если  - дискретная случайная величина, принимающая бесконечное, но счетное число значений, то

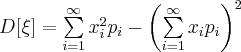 (25)

Если  - непрерывная случайная величина, принимающая значения на конечном промежутке , то

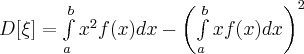 (26)

Если  непрерывная случайная величина, принимающая значения на всей числовой оси, то

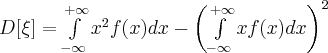 (27)

Дисперсия является характеристикой рассеивания возможных значений случайной величины, но она лишена  наглядности, так как имеет размерность квадрата случайной величины. Характеристикой рассеивания  случайной величины, совпадающей по размерности со случайной величиной, является среднее квадратичное  отклонение.

Определение 12. Средним квадратичным отклонением случайной величины называется корень квадратный из дисперсии.

 (28)

Пример 13. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины  - числа появлений некоторого события  в одном испытании, если вероятность появления события  в одном испытании равна 0,8. Решение. Случайная величина  является дискретной случайной величиной, она принимает два значения: 0 с вероятностью 1-0,8=0,2 и 1 с вероятностью 0,8. Тогда ряд распределения данной случайной величины будет иметь вид:

	0	1
	0,2	0,8

Сначала найдем математическое ожидание по формуле , тогда  . Теперь вычислим дисперсию, используя формулу (19): . Тогда среднее квадратичное отклонение равно: . Вопрос. Дисперсия случайной величины - это неотрицательное число.

неверно

верно

Начальные и центральные моменты случайной величины

Обобщением основных числовых характеристик случайной величины являются понятия моментов. Название заимствовано из механики, где эти понятия применяются для описания распределения масс. Определение 13. Начальным моментом k-го порядка случайной величины  называется математическое ожидание случайной величины .

 (29)

Если  - дискретная случайная величина, принимающая конечное число значений, то

 (30)

Если  - дискретная случайная величина, принимающая бесконечное, но счетное число значений, то

 (31)

Если  - непрерывная случайная величина, принимающая значение на конечном промежутке , то

 (32)

Если  - непрерывная случайная величина, принимающая значения на всей числовой оси, то

 (33)

Начальный момент 1-го порядка - это математическое ожидание случайной величины: . Начальные моменты высших порядков главным образом используются для вычисления центральных моментов. Определение 14. Центральным моментом k-го порядка случайной величины  называется математическое ожидание случайной величины .

 (34)

Если случайная величина  - дискретная, принимающая конечное число значений, то

 (35)

Если случайная величина  - дискретная, принимающая бесконечное, но счетное число значений, то

 (36)

Если случайная величина  - непрерывная, принимающая значения на конечном промежутке , то

 (37)

Если случайная величина  - непрерывная, принимающая значения на всей числовой оси, то

 (38)

1. Центральный момент 1-го порядка равен нулю: . 2. Центральный момент 2-го порядка - это дисперсия случайной величины: . 3. Центральный момент 3-го порядка служит характеристикой асимметрии(" скошенности") распределения. Если распределение случайной величины  - симметричное, то . Число, которое находится по формуле :

 (39)

называется коэффициентом асимметрии.  Если , то распределение имеет левостороннюю "скошенность", график плотности распределения имеет вид:

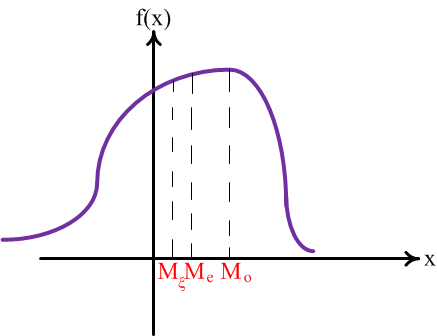
Рис.11

Тогда . Если , то распределение имеет правостороннюю "скошенность", график плотности распределения в этом случае имеет вид:

Рис.12

Тогда .

4. Центральный момент 4-го порядка служит характеристикой "островершинности" или "плосковершинности" распределения. Эти свойства распределения описываются с помощью эксцесса, который вычисляется по формуле:

 (40)

Для наиболее распространенного нормального распределения(подробно о котором будет изложено в лекции "Законы распределения случайных величин") . Кривая нормального распределения принята за эталон, остальные с ней сравниваются. Для "островершинных" распределения , для "плосковершинных" распределений (см. рис.13):

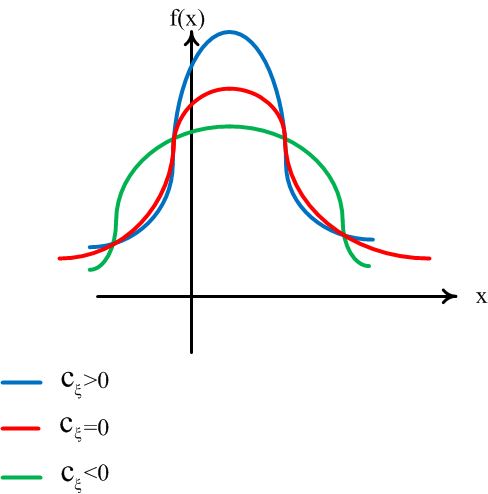
Рис.13

Пример 14. Дискретная случайная величина  задана рядом распределения:

	1	2
	0,4	0,6

Найти центральные моменты 1-го, 2-го и 3-го порядков.

Решение. Сначала найдем начальный момент 1-го порядка, то есть математическое ожидание случайной величины, получаем:. Центральный момент 1-го порядка равен 0. Центральный момент 2-го порядка - это дисперсия случайной величины, вычисляем ее по формуле (35): . Аналогично по формуле (35) вычисляем центральный момент 3-го порядка: .

Вопрос. Центральный момент 3-го порядка , тогда коэффициент асимметрии : а) больше нуля; б) меньше нуля; в) равен нулю; г) невозможно ответить на этот вопрос.

б)

в)

г)

а)