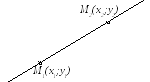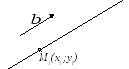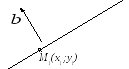ОПД.Ф.13. Компьютерная геометрия и графика
-
Взаимосвязь уравнений прямой на плоскости.
1. Точка
Точку на плоскости задают парой чисел (x;y), в трехмерном пространстве - тремя числами (x;y;z).
2. Прямая на плоскости
Прямая состоит из бесконечного числа точек. Прямую задает уравнение – некоторое условие, которому удовлетворяют все точки прямой.
Свойства векторов позволяют записать уравнения прямой.
Рассмотрим свойство параллельности векторов.
1. Через две точки можно провести единственную прямую.
|
|
Уравнение
имеет вид:
и вытекает из условия коллинеарности векторов:
|
2. Через точку можно построить прямую параллельно некоторому вектору. В этом случае уравнение называется каноническим.
|
|
Уравнение
имеет вид:
и также является условием коллинеарности двух векторов:
|
.
Условия 1 и 2 можно записать в параметрическом виде:
.
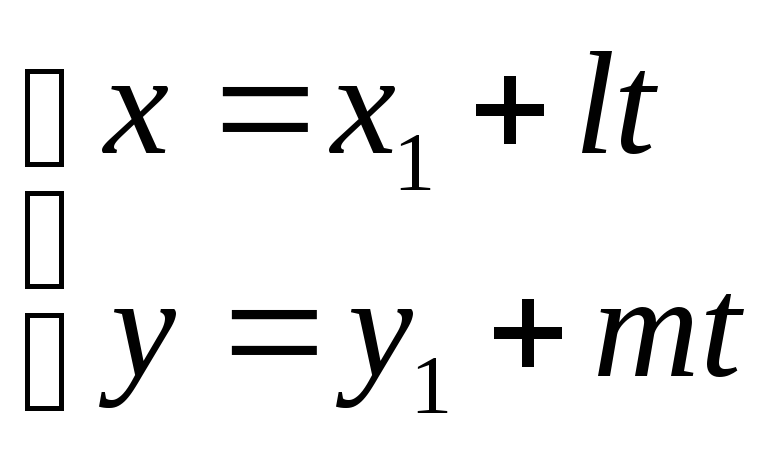Здесь t – некоторый параметр.
3. Через точку можно построить прямую перпендикулярно некоторому вектору. В этом случае уравнение называется общим.
|
|
Уравнение
имеет вид:
или
и вытекает из условия ортогональности двух векторов:
|
.Общее уравнение можно записать в нормированном виде:
.
Знак μ выбирают противоположным знаку коэффициента D.
Такие условия, в зависимости от имеющихся исходных данных, можно записывать в самых разных видах.
Отклонение δ точки M(x0;y0) от прямой вычисляется по формуле:
.
Расстояние d
точки M(x0;y0)
до прямой равно модулю отклонения
.
Таблица 1
Взаимосвязи уравнений прямой на плоскости
|
Исходное уравнение |
Полученное уравнение |
Связь параметров уравнений |
|
Каноническое
|
Общее
|
A=l, B=-m, D=-mx1+ly1 |
|
Каноническое
|
С угловым коэффициентом y–y1=k(x-x1), y=kx+b |
|
|
Общее A(x-x1)+B(y-y1)=0 |
Каноническое
|
l=-B/A, m=1 |
|
Общее
|
"В отрезках"
|
a=-D/A, b=-D/B |
|
Общее Ax+By+D=0 |
С угловым коэффициентом y=kx+b |
k=-A/B, b=-D/B |
|
Общее
Ax + By + C = 0 |
Нормированное
|
|
2. Уравнения плоскости
Общее уравнение плоскости имеет вид
.
Построение плоскости
означает определение параметров
.
Все другие виды уравнения плоскости
легко получить из общего уравнения.
Рассмотрим
простейший способ вычисления параметров
.
Пусть заданы точка
,
лежащая на искомой плоскости, и вектор
,
ортогональный искомой плоскости.
Для поиска параметров
воспользуемся тем, что вектор
ортогонален любому вектору
,
лежащему на искомой плоскости.
Из условия
ортогональности векторов (их скалярное
произведение равно нулю:
)
получаем:
Здесь
.
Нормированное уравнение плоскости
из общего уравнения получается путем замен
.
Знак μ выбирается противоположным знаку D.
Здесь (α, β, γ) – направляющие углы вектора, перпендикулярного искомой плоскости (этот вектор направлен от начала координат в сторону плоскости), и p – расстояние от начала координат до плоскости.
Так же можно
получить уравнение
плоскости в отрезках,
если известны
три отрезка
,
отсекаемые плоскостью на осях координат:
.
Это уравнение легко можно получить и из общего уравнения, приняв:
a=-D/A, b=-D/B, c=-D/C.
Рассмотрим более сложные в смысле расчетов построения плоскости.
Известна аксиома
– через три разные точки
,
и
можно построить единственную плоскость.
Есть разные способы построения этой плоскости.
Способ 1.
Векторы
и
параллельны искомой
плоскости. Их векторное произведение
ортогонально
искомой плоскости.
Тогда получили
задачу построения плоскости, проходящей
через точку
перпендикулярно вектору
.
Это построение рассмотрено выше.
Способ 2.
Использовать компланарность векторов
,
и
:
.
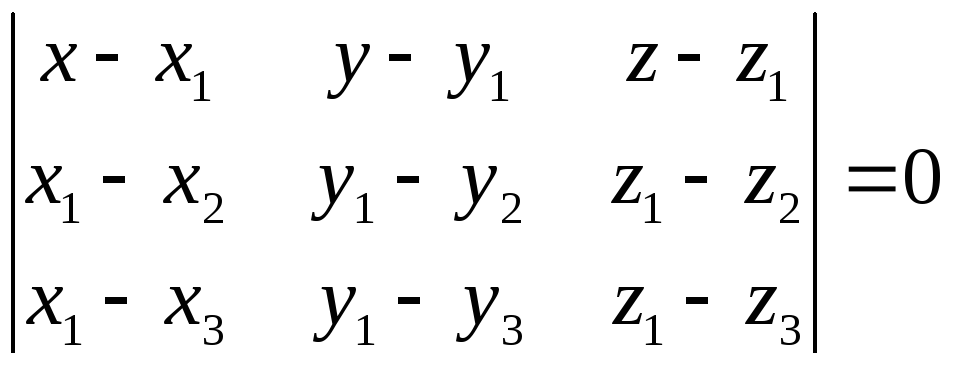Раскрыв этот определитель, можно получить общее уравнение плоскости:
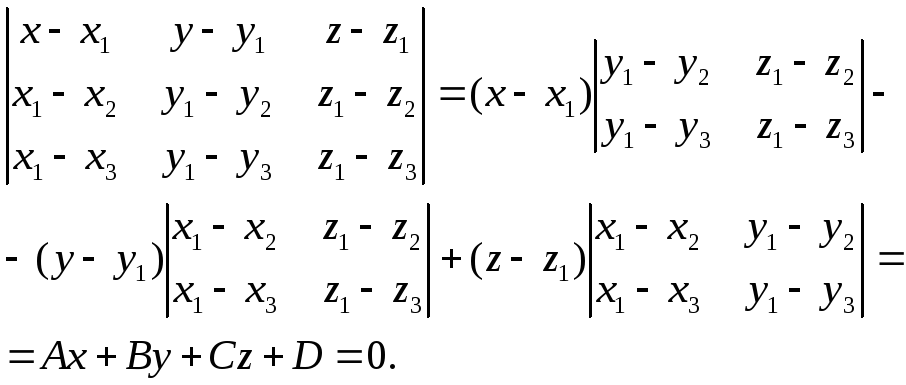
Здесь
,
,
,
Условие компланарности является универсальным методом построения плоскости при различных исходных данных.