Поиск направления на минимум при минимизации функционала качества в трехмерном вариационном анализе

Метод наискорейшего спуска действует в направлении отрицательного локального градиента. Это направление не всегда совпадает с направлением на минимум функционала качества. Чаще всего это направление в сторону от минимума, поэтому приходится делать несколько итераций, чтобы достигнуть минимального значения. В результате метод наискорейшего спуска может стать неэффективным. Если определить направление на минимум, то алгоритм наискорейшего спуска станет более эффективным.

Одним из методов является замена переменных с целью получения концентрических окружностей вместо эллипсов. Так в приведенном выше примере можно сделать замену . Тогда уравнение для функционала качества в новых переменных будет, т.е. уравнение окружности. Теперь градиент будет всегда направлен к центру, т.е. в сторону минимальных значений.

Другой способ предполагает вычисление направления на минимум. Функционал качества представляет собой число (скаляр), полученное в результате суммирования по всем узлам и станциям

Градиент (вектор размерности ) получается в результате варьирования (дифференцирования) по каждому,:

Если теперь взять вторую вариацию по каждому , то получится матрица размерности, называемая матрицей Хесса

Если теперь разложить функционал качества в ряд Тейлора вблизи точки анализа :

И проварьировать относительно и приравнять нулю, то получим

Откуда

Произвольное направление в пространстве функций может быть определено как

Где произвольная матрица размерности. Если эта матрица единичная, то получается направление наискорейшего спуска.

Возьмем теперь в качестве матрицы, определяющей направление вторую производную от функционала качества:

Это будет матрица размерности , где- число узлов модельной сетки.

Подобная матрица называется матрицей Хесса.

Рассмотрим теперь алгоритм спуска в виде

Где - длина шага.

Подставив выражения для градиента и матрицы Хесса функционала качества и полагая единичный шаг и линейность оператора наблюдений получим алгоритм Ньютоновского спуска

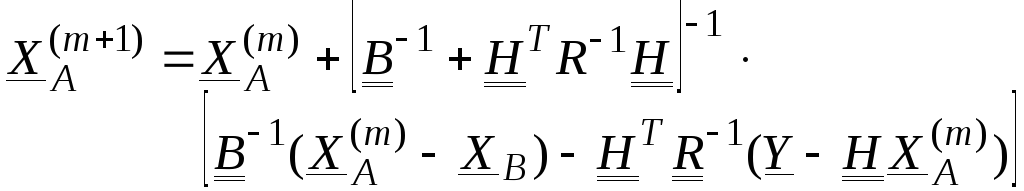
Где - номер итерации.

Четырехмерная вариационная ассимиляция (4d-Var) Постановка задачи четырехмерной ассимиляции

Четырехмерность 4D-Var отражает тот факт, что при анализе учитывается распределение измерений не только в пространстве, но и во времени. Основная идея заключается в том, что оптимальный анализ должен соответствовать не только самим измерениям, но и их изменчивости во времени, которая определяется физическими законами и описывается модельными эволюционными уравнениями. Подобный оптимальный анализ, по сути, представляет собой обратную задачу. Действительно, гидродинамическая модель создается для решения прямой задачи, что означает, что если задать начальные условия и применить к ним модельные уравнения, то мы получим прогноз распределения метеопараметров, которые фактически наблюдаются. Примером такой модели является интерполяция метеорологических параметров (температура, скорости ветра, влажность и др.) с модельной сетки в точки наблюдений и к срокам наблюдений. В зависимости от качества модели и начальных условий подобные «предсказанные наблюдения» могут соответствовать или не соответствовать фактическим наблюдениям. Таким образом, можно сформулировать обратную задачу, как поиск таких начальных условий, которые при использовании данной конкретной модели прогноза погоды дают наилучший прогноз фактических наблюдений. Решить подобную обратную задачу намного сложнее, чем соответствующую ей прямую задачу, т.к. для выбора наилучшего приближения к измерениям нужно несколько раз решать прямую задачу (запускать модель) от меняющихся начальных условий (итерационная процедура).

Рисунок 1. Модельный прогноз наблюдаемой переменной (кривая). Наблюдения показаны с учетом их неопределенности (вертикальные линии). Четырехмерное усвоение представляет собой подбор таких начальных условий (жирная вертикальная полоска в ), стартуя от которых модель дает наилучшее приближение к наблюдениям (остальные полоски).

Задача решается как проблема оптимизации. При решении этой проблемы нужно учитывать следующее:

1. Оптимальное решение должно теперь соответствовать не только измерениям и результатам фоновых оценок, но и физическим и другим законам, определяющим временную изменчивость в модели;

2. Нужно учитывать ошибки измерений и моделирования и их корреляции в пространстве и времени;

3. Оптимальное решение должно быть и в регионах с малым покрытием данными и в местах их отсутствия.

Оптимизация может рассматриваться как тип решения обратной задачи. Если предположить, что прямая задача имеет решение, то, имея начальные данные, можно с помощью прямой модели получить распределение моделируемых параметров в любой момент времени. Обратная задача может быть сформулирована как следующая: какой набор начальных условий в результате моделирования приводит к лучшему предсказанию имеющихся наблюдений. Обратную задачу решить намного сложнее, чем прямую, т.к. нужно несколько раз пропускать модель с разными начальными условиями.