1.6. Интерполяционная формула Ньютона для неравноотстоящих узлов

Для построения интерполяционных формул, имеющих перед классической интерполяционной формулой Лагранжа (1.6) преимущества, какими обладают конечноразностные формулы, и

применимых в более общем по сравнению с последними случае произвольного расположения упорядоченных несовпадающих узлов х₀, x₁, ..., х_п на промежутке [а, b], вместо конечных разностей используют разделенные разности, или иначе, разностные отношения.

Через значения функции f(x₀), f(x), ···, f(x_n) сначала определяют разделенные разности первого порядка:

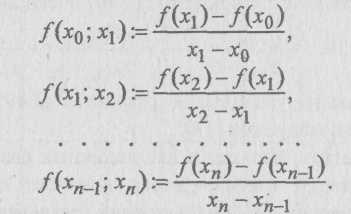
На этих разностях базируются разделенные разности второго порядка:

и т.д. Таким образом, если определены k-e разностные отношения f(x_i,·; х_i+1;...; x_i+k), то (k + 1)-е определяются через них равенством

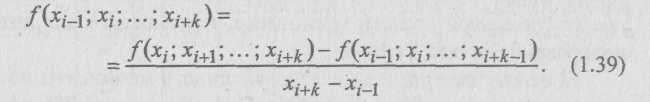
Легко проверить, что операция взятия разделенной разности, как и в случае конечной разности, аддитивна и однородна, т.е. линейна. Кроме того, разделенная разность есть симметрическая функция своих аргументов, что позволяет у разделенной разности менять аргументы местами.

Доказательство симметричности опирается на представление к-й разделенной разности через значения функции в узлах, имеющее вид

При к = \ справедливость выражения (1.4.0) очевидна:

Для произвольных натуральных к равенство (1.40) доказывается на основе (1.39) по индукции [14].

Важно отметить, что как и для конечных разностей, взятие разделенной разности многочлена понижает на единицу его степень. Это следует из рассмотрения разделенной разности

Отсюда приходим к заключению, что разделенные разности η-го порядка многочлена n-й степени

постоянны'. ,

Следовательно, как и в конечноразностном случае, анализируя таблицу разделенных разностей (табл. 1.8), по порядку почти совпадающих разделенных разностей можно сделать вывод о предпочтительной степени многочлена, подходящего для интерполирования данной функции.

В основу построения интерполяционного многочлена по типу первого интерполяционного многочлена Ньютона (1.25), но для случая неравных промежутков между узлами x_it положим следующие рассуждения.

Таблица 1.8 Таблица разделенных разностей

Пусть φ(χ) — некоторая функция с известными значениями в узлах х_о,х₁,..., а х — произвольная фиксированная точка. По определению разделенной разности первого порядка имеем

откуда

Для разделенной разности второго порядка по точкам x, x₀, x₁ записываем представление

следствием которого является выражение

Подставляя его в (1.41), приходим к равенству

Формально, на основе определяющего разделенные разности рекуррентного соотношения (1.39), этот процесс может быть продолжен. В результате можно записать формулу, описывающую своеобразное разложение φ(x) по произведениям разностей (х -x_i), коэффициентами в котором являются разделенные разности различных порядков:

Если φ(x)  Р_п (х) — многочлен степени n, то процесс подобного разложения исчерпывается. Разложение будет состоять из n+1 слагаемого, и все они будут иметь конкретные коэффициенты, так как последняя, содержащая х, разделенная разность в (1.42), т.е. φ(x;x_ο;...;x_η) = Ρ_n(x;x_ο;...;x_η) имеет (n + 1)-й порядок и, значит, равна нулю. Таким образом, для любого

многочлена степени n справедливо тождество

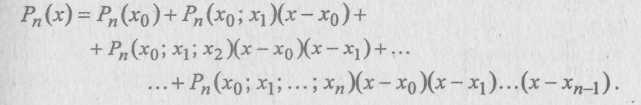
Предположим, что этот многочлен Р_n(х) является интерполяционным для некоторой функции f(x). Тогда во всех узлах x₀, x₁, ..., х_п он должен иметь одинаковые с ней значения, а значит должны быть одинаковыми и их разделенные разности. Отсюда приходим к интерполяционной формуле Ньютона для неравноотстоящих узлов:

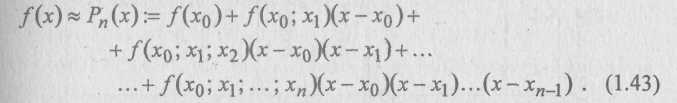
Подставив f(x) вместо (х) в (1.42), с учетом (1.43) получаем точное равенство

второе слагаемое в котором может рассматриваться в качестве остаточного члена, т.е.

где П_п+1(х) —многочлен, введенный ранее посредством (1.10).

Поскольку для вычисления разности f(x; x₀;…;x_n) требуется знание значения f(x) наряду с известными значениями f(x₀), f(x_n), представляемое формулой (1.44) выражение R_n (χ) фактически можно использовать только для оценивания погрешности интерполирования по формуле (1.43) через максимальные величины модулей разделенных разностей (n + 1)-го порядка (если в них содержится достаточно незашумленной информации) или для получения других выражений остаточного члена при тех или иных предположениях о данной функции. В частности, если функция f{x) имеет (n + 1)-ю производную, то остаточный член (1.44) может быть преобразован к виду (1.12), согласно утверждению о единственности интерполяционного многочлена Лагранжа, одной из форм представления которого является (1.43).

Таблица 1.9 Разделенные разности функции / (jc) = cos (e~^x)

При практическом использовании интерполяционной формулы (1.43) приходится полагаться на убывание модулей слагаемых в Р„ (х) при увеличении номера слагаемого. Такое убывание обычно происходит до некоторых пор; затем начинается рост их модулей из-за влияния ошибок округления.

Заметим, что при использовании разделенных разностей, как и при конечноразностной интерполяции, можно менять последовательность подключения узлов и получать интерполяционные формулы для неравных промежутков, отличные от (1.43), но имеющие такую же структуру.

1.7. Обратное интерполирование

Под задачей обратного интерполирования понимается задача нахождения приближенного значения аргумента χ таблично заданной функции f(x), соответствующего некоторому известному значению у этой функции. При этом, естественно, предполагается, что у не совпадает ни с одним из данных значений y_i = f(x_i) (и значит, χ не совпадает ни с одним из узлов x_t) и, в то же время, достаточно хорошо «вписывается» в таблицу значений у,.

Для того чтобы говорить о теоретически однозначной разрешимости задачи обратного интерполирования, нужно потребовать, чтобы было выполнено основное условие существования обратной функции x = f^-1{y) — монотонность данной сеточной функции. Условимся далее считать, что такая монотонность имеет место либо во всей исходной таблице значений y_t, либо в некоторой ее части (используемой для решения обратной задачи).

Так как функция у = f(x), вообще говоря, не может быть восстановлена точно по нескольким своим значениям (за определенными исключениями), то и обратная задача заведомо может решаться лишь приближенно.

Формально простейший из приемов решения задачи обратной интерполяции заключается в перемене ролями функции и аргумента и применения интерполяционной формулы Лагранжа, т.е. непосредственное вычисление χ по формуле (ср. (1.6))

Такой подход обладает характерными для применений формулы Лагранжа недостатками (обсужденными ранее, см., в частности, §1.3) и привлекателен лишь в случаях, когда степень η интерполяционного многочлена невысока и заранее известна.

Например, им можно воспользоваться для следующего вывода метода обратной линейной интерполяции (иначе, метода хорд) решения скалярных уравнений вида f(x) = 0 [23 и др.].

Пусть для непрерывной функции у = f(x) известны две точки х₀, x₁ такие, что f(x₀).f{x₁)<0, т.е. между ними имеется точка χ такая, что у^=f(х^) = 0. Приближенно эту точку можно найти обратной линейной интерполяцией, подставив в (1.45) n = 1 и у^ =0: '

Обозначая правую часть этого приближенного равенства через x₂ и учитывая, что у₀ = f(x₀ ), у₁ = f(x₁), полученному придаем вид

На основе последней формулы (возможно, более узнаваемой в виде

строится итерационный процесс получения последовательных приближений x_k к корню х^ уравнения f(х) = 0 (см. рис. 1.3, а также [23]).

Рис. 1.3. Приближения к корню χ уравнения f(x) = 0 методом обратной линейной интерполяции

Используя сразу большее, чем в предыдущем случае, количество точечной информации о данной функции f(x), т.е. подменяя функцию f(x) интерполяционным многочленом Р_п(х) достаточно высокой степени, можно за один шаг найти удовлетворительное приближение к искомому значению χ^ = f^-1 (у) и, в частности, при у^ = 0 с хорошей точностью найти корень уравнения f(x) = 0;

Если сопрягать точность получения искомого значения х = f^-1 (у) с построением соответствующего интерполяционного многочлена подходящей (неизвестной заранее) степени, то для этой цели более пригодны интерполяционные формулы, в которых можно постепенно наращивать точность за счет последовательного подключения все новых узлов. Рассмотрим, как это может быть реализовано в случае, когда информация об f(x) берется на системе равноотстоящих узлов.

Предположим, что число у^ близко к у₀ =f(x₀), например, вписывается между у₀ и у₁ = f(x₁), и пусть известно достаточное количество значений y_i функции f(x) в точках х_i =x₀ + ih

при i = 0,1,2,... . Тогда за основу может быть принята первая интерполяционная формула Ньютона (1.26) с базовым узлом x₀. В силу выдвинутого ранее требования о монотонности f{x), искомая точка χ^ должна быть близка к х₀; следовательно, приближенное значение χ^ будет найдено, если удастся найти такое (вообще говоря, малое, укладывающееся в границы интервала (0,1)) значение

которое является приближенным корнем уравнения

Учитывая специфику уравнения (1.46), придадим ему вид задачи о неподвижной точке

К последнему можно применить метод простых итераций [23], т.е. находить последовательные приближения q_k к q по формуле

при k = 0,1, 2,..., начиная с

степень интерполяционного многочлена здесь фиксируется в соответствии с поведением конечных разностей (не обязательно сразу максимальная; можно ее наращивать постепенно от итерации к итерации), а число итераций к, при котором следует положить q^:q_k, определяется практическим совпадением q_k с q_k-1 в пределах тех знаков, на которые можно рассчитывать при той или иной точности и разреженности исходной дискретной информации об f(x). После того, как при некотором k  1 будет принято q^:q_k , считаем χ^:« x0 + q^h.

Для решения задачи обратной интерполяции можно составить и другие аналогичные (1.46) уравнения с помощью подходящих для того или иного случая разностных интерполяционных формул. Например, на базе интерполяционной формулы Ньютона для неравноотстоящих промежутков (1.43) можно построить итерационный процесс вычисления последовательных приближений х^(k) к искомому значению χ^ по формуле

где

Процесс подключения слагаемых в правой части, содержащих разделенные разности все более высоких порядков, здесь также может быть организован последовательным.

Таблица 1.10