1. Множества и операции над ними. Свойства операций.

Множества – это совокупность элементов, объединённых общими свойствами.

Принадлежность элемента множеству:

• –принадлежность элемента aк множеству A

• a ₵ A – непринадлежность элемента aк мноеству A

• A U B – объединение множеств, или множество С с элементами множеств Aи B

• - пересечение множеств, или множество С с общими элементами Aи В

• A \ B – разность двух множеств, или множество C , которое состоит из элементов множества A , которых нет в множестве B.

• –симметрическая разность двух множеств, или множество C , которое состоит из не общих элементов множеств A и B.

• С_uA = Ā –дополнение множества, или множество Aявляется множеством U,тогда определяется операция дополнения - СuA = Ā = U\A

• A C B – вхождение одного множества в другое множество, или если любой элемент множества A является элементом множества B , то говорят, что множество A есть подмножество множества B (множество A входит в множество B ).

• A ₵ B - Не вхождение одного множества в другое множество, или если существует элемент множества A , который не является элементом множества B , то говорят, что множество A не подмножество множества B.

Свойства операций над множествами.

2. Множества вещественных чисел. Свойства операций над ними и геометрическая интерпретация.

Вещественное число - это любое положительное число, отрицательное число или нуль.

• Вещественные числа можно складывать, и при этом выполняются следующие законы:

(коммутативный)(ассоциативный)

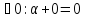(существование нуля)

= 0 (существование противоположного элемента)

-

• Вещественные числа можно перемножать, и при этом выполняются следующие законы:

(коммутативный)

(ассоциативный)

(существование единицы)

Приме: и

• Каждое вещественное число, отличное от нуля, либо положительно, либо отрицательно. При этом сумма и произведение положительных чисел — положительное числа.

• Каждое вещественное число, отличное от нуля, либо положительно, либо отрицательно. При этом сумма и произведение положительных чисел — положительное числа.

Геометрическая интерпретация вещественных чисел: каждой точке числовой оси 0x ставится в соответствие вещественное число x, и обратно, каждому вещественному числу x соответствует единственная точка числовой оси.

3. Функции. Определение и общие свойства.

Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной.

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.

Свойста:

1) Область определения функции и область значений функции.

1. Область определения функции - это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.

2. Область значений функции - это множество всех действительных значений y, которые принимает функция.

3. Нули функции. Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

4. Промежутки знакопостоянства функции. Промежутки функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

5. Монотонность функции. Возрастающая функция. Убывающая функция.

6. Чётность (нечётность) функции. Чётная функция - функция, у которой область определения симметрична относительно начала координат. График чётной функции симметричен относительно оси ординат. Нечётная функция - функция, у которой область определения симметрична относительно начала координат. График нечётной функции симметричен относительно начала координат.

7. Ограниченность функции. Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция - неограниченная.

8. Периодическость функции. Функция f(x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

4. Числовые последовательности. Определение. Что такое ограниченная неограниченная последовательность.

Числовая последовательность— это последовательность элементов числового пространства

Определение: Пусть множество X — это либо множество вещественных чисел R, тогда последовательность элементов множества X называетсячисловой последовательностью.

Ограниченная и неограниченная последовательность.

Последовательность {xn} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство: <M т.е. все члены последовательности принадлежат промежутку (-М; M).

Последовательность {xn}называется ограниченной сверху, если для любого n существует такое число М, чтоxn ≤ M.

Последовательность {xn}называется ограниченной снизу, если для любого n существует такое число М, что xn ≥ M

5. Предел числовой последовательности. Теорема. Свойства предела.

Число а называется пределом последовательности {xn}, если для любого положительного >0 существует такой номер N, что для всех n > N выполняется условие: Это записывается: lim xn = a.

В этом случае говорят, что последовательность {xn}сходится к а при n→∞.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример.Доказать, что предел последовательности lim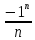= 0

Пусть при n > N верно 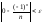, т.е.. Это верно при, таким образом, если за N взять целую часть от, то утверждение, приведенное выше, выполняется.

Пример.Показать, что при n →∞ последовательность 3,имеет пределом число 2.

Итого: {xn}= 2 + 1/n; 1/n = xn – 2

Очевидно, что существует такое число n, что , т.е. lim {xn} = 2.

Теорема. Последовательность не может иметь более одного предела.

Теорема. Если (xn)→ a, то

Теорема. Если (xn) → a, то последовательность {xn} ограничена.

6. Предел функции и его свойства. Односторонние пределы.

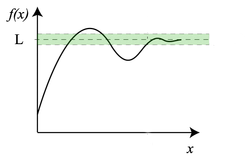
Предел функции — одно из основных понятий математического анализа. Функция f(x) имеет предел L в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к L.

Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).

Предел функции обозначается как .

Свойства пределов функции

1. Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

2) Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Аналогично предел разности двух функций равен разности пределов этих функций.

Расширенное свойство предела суммы:

Предел суммы нескольких функций равен сумме пределов этих функций:

Аналогично предел разности нескольких функций равен разности пределов этих функций.

3) Предел произведения функции на постоянную величину

Постоянный коэффициэнт можно выносить за знак предела:

4) Предел произведения

Предел произведения двух функций равен произведению пределов этих функций:

Расширенное свойство предела произведения

Предел произведения нескольких функций равен произведению пределов этих функций:

5) Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Односторонние пределы

Пусть на некотором числовоммножествезаданачисловая функцияи число—предельная точкаобласти определения.

7. Замечательные пределы. Виды неопределённостей и как они раскрываются.

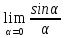1)=1 ->

2) y=f(x) ->

Выше предоставлены 2 замечательных предела!!!

Виды неопределённостей и как они раскрываются

8. Бесконечно малые и бесконечно большие функции. Таблица эквивалентностей.

• Y=f(x) def бесконечно малой при x->x0 ,если lim f(x) = 0!

Пример: lim x-> 1 (x^3-1) = 0 => x^3-1 –б.м.ф при x ->1

• Y=f(x) def бесконечно большой при x->x0,если lim x->x0 f(x) =∞!!!

Пример: lim x-> 0 1/x = ∞ => 1/x ->б.б.ф

Если(x)и –б.м.ф , то (x) –б.м.ф, аналогично с перемножением и умножением на const!

Сравнение б.м.ф и б.б.ф

• a(x) , b(x) – б.м.ф, то = constтогда a(x)и b(x)одного порядка малости.

• =0тогда a(x) –бесконечно малая более высокого порядка.

• Если lim = ∞тогда b(x) –бесконечно малая более высокого порядка.

• Если lim =1 –тогда a(x) и b(x)эквивалентны.

Таблица эквивалентностей:

9. Непрерывность функций. Точки разрыва.

f(x) def непрерывной в точке x0 , если:

• она определена функцией

• односторонние пределы существуют и равны + равны значения функций в этой точке.

Функция непрерывна на промежутке , если она не прерывна в каждой точке этой f(x)!

Если все условия не выполняются – в этой точке нет непрерывности!

1. lim x-> x0-0 f(x) ≠lim x0=->x0+0 f(x) -> тогда x0 –точка разрыва первого рода.

2. Если хотя бы один из одностороннего предела не существует, тогда x0 –точка разрыва второго рода. + x=x0 – асинтода. F(x) = 1/x

3. Оба предела существуют и равны между собой. Lim x->x-0 f(x) = lim x-> x+0 f(x),тогда x0 –точка устранимого разрыва.

10. Локальные свойства непрерывных функций.

Л.Ф – наз. такие свойства ф-ий , кот опред. поведение ф-ии в сколько угодно малой окрестности в любой точке определения.

1 Теорема – если y=f(x) непрерывна в точкеx0 ,то она обязательно ограничена в какой т окрестности этой точки.

2 Теорема – если y=f(x)непрерывна в точке x0и y(x0) ≠0,то некоторой окрестност этой точки x0все значения ф-ии либо + либо - !!!

3. Теорема – f(x) + g(x) –если эти 2 функции непрерывны в точке x0,значит в этой точке непрерывна их сумма(разность, произведение и т.д)

4 Теорема – если -U=U(x) имеет предел в точке x0 равный A, то ф-ия y=f(U(x))непрерывна. Lim =

5 Теорема (непрерывность сложной ф-ии) – если U=U(x)непрерывна в точке x0,а y=f(U)непрерывна в точке U0,тогда тогда сложная ф-ия y=f(U(x))также будет непрерывна в точке x0.

11. Глобальные свойства непрерывных ф-ий

Г.С – наз. такое свойство , кот связано со всей областью определения.

Ф-ия y=f(x)наз. непрерывной на интерволь (a;b)если она непрерывна в каждой точке этого промежутка.

Теорема 1 (Коши о существовании корня). Если функция, непрерывная на отрезке [a, b], принимает на его концах значения разных знаков (f (a) • f (b) < 0), то на отрезке существует такая точка x0, что f (x0) = 0.

Теорема 2 (Больцано-Коши о промежуточном значении). Если функция

g : [a, b] → R непрерывна на [a, b], g(a) = A, g(b) = B, то для любого числа C,

лежащего между A и B, найдется точка c ∈ [a, b], в которой g(c) = C.

Теорема 3 (первая теорема Вейерштрасса). Функция, непрерывная на отрезке, ограничена на нем.

Теорема 4 (вторая теорема Вейерштрасса). Функция, непрерывная на

отрезке, принимает на этом отрезке свое максимальное и минимальное значение.

12. Производные функции. Геометрические и физические свойства. Определение слева справа.

!!!Производной F(x) в точке x0 называется пределом (если он существует) отношением приращения f(x) к 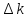. (при условии x -> 0).

Y’(x0) = f’(x0) = lim x ->0

Дифференцирование – процесс нахождения производной функции.

Физическая производная – скорость движения точки в момент времени x0.

Геометрический смысл производной – геометрическая величина производной представляет собой угловой коэфициент касательной кривой y=f(x)точке с координатами x0и f(x0).

Пример в тетради!!!

Если предел сущ, функция y=(fx)наз. дифференцированной в точке x0, тогда необходимым уловием диф функци в точке явл её непрерывность.

Если б то f’ +

Если то f’-

13. Таблица производных и правило дифференцирования.

Правила дифференцирования.

Пусть f(x) +g(x) –диф. Функ.

1. (f(x) ±g(x))’ = f’(x) ± g’(x) –линейность

2. [A x f(x)]’ = A x f’(x), где A – const.

3. [f(x) x g(x)]’ = f’(x) x g(x) + f(x) + g’(x)

4. =

5. , U = £(x)=> y = f(£(x) тогда y’ = Fu’ x U’

Производная обратной функции: Пусть y=f(x)дифференцированная на (a;b)и имеет непрерывную обратную функцию x=g(y).Если f’(x)≠0,то существует производная обратной функции –> x’y = 1/f’x.

Производная параметрической ф-ии.

Y=f(x)

Y’(x) =

Производная неявно заданной функции.

F(x,y) = 0 – неявное задание ф-ии.

Диф-ется => (tgx/y +x^2-y)’ = (5)’ y=y(x)!!!

14. Дифференциал функции. Определение и свойства.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.

Основные дифференциалы:

Дифференциал функции обладает свойствами, аналогичными свойствам производной.

1. Дифференциал постоянной равен нулю: dc = 0, с = const.

2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:

d(u+v)=du + dv

Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны

d(u+c) = du (c= const).

3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:

d(uv) = udv + vdu.

Следствие. Постоянный множитель можно выносить за знак дифференциала

d(cu) = cdu (с = const).

4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой

5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

15. Производные и дифференциалы высших порядков.

Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом,

f"(x) = (f'(x))'.

Если дифференцируема (n - 1)-я производная функции f, то ее n-й производной называется производная от (n - 1)-й производной функции f и обозначается f⁽ⁿ⁾. Итак,

f⁽ⁿ⁾(x) = (f^(n-1)(x))',   n ϵ N,   f⁽⁰⁾(x) = f(x).

Число n называется порядком производной.

Дифференциалом n-го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом,

dⁿf(x) = d(d^n-1f(x)),   d⁰f(x) = f(x),   n ϵ N.

Если x - независимая переменная, то

dx = const   и   d²x = d³x = ... = dⁿx = 0.

В этом случае справедлива формула

dⁿf(x) = f⁽ⁿ⁾(x)(dx)ⁿ.

Производные n-го порядка от основных элементарных функций

Справедливы формулы

16. Применение производных к исследованию функций.

Основные теоремы дифференцирования функций:

Теорема Ролля

Пусть функция f: [a, b] → R непрерывна на сегменте [a, b], и имеет конечную или бесконечную производную внутри этого сегмента. Пусть, кроме того, f(a) = f(b). Тогда внутри сегмента [a, b] найдется точка ξ такая, что f'(ξ) = 0.

Теорема Лагранжа

Если функция f: [a, b] → R непрерывна на сегменте [a, b] и имеет конечную или бесконечную производную во внутренних точках этого сегмента, то такое, чтоf(b) - f(a) = f'(ξ)(b - a).

Теорема Коши

Если каждая из функций f и g непрерывна на [a, b] и имеет конечную или бесконечную производную на ]a, b[ и если, кроме того, производная g'(x) ≠ 0 на ]a, b[, то такое, что справедлива формула

Если дополнительно потребовать, чтобы g(a) ≠ g(b), то условие g'(x) ≠ 0 можно заменить менее жестким:

17. Возрастающие и убывающие функции. Экстремумы.

Интервалы монотонности. Экстремумы

Функция у = f (х) называется возрастающей (убывающей) на некотором промежутке, если для любых значений x₂>x₁ этого промежутка выполняется условие f(x₂) > f(x₁)(f (x₂) < f (x₁)).

Функция у = f(х) имеет максимум (минимум) в точке x₀, если существует такая окрестность точки x₀, что для всех x, принадлежащих этой окрестности, выпол­няется условие f(х) < f(х₀) (f (х) > f(х₀), х х₀.

Максимумы и минимумы функции называются ее экстремумами.

Интервал, на котором функция возрастает или убывает, называется интервалом монотонности функции.

18. Выпуклость и вогнутость графика функции Точки перегиба.

График дифференцируемой функции у = f(x) называется выпуклым (вогнутым) в интервале (а,b), если он расположен ниже (выше) любой своей касательной на этом интервале.

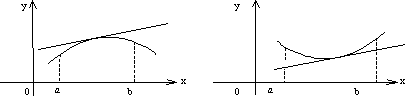
Точка графика непрерывной функции, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба.

Теорема 5. (достаточный признак выпуклости и вогнутости). Пусть функция у = f(x) имеет вторую производную (x) во всех точках интервала (а_, b). Если во всех точках этого интервала < 0, то график в (а_, b) выпуклый; если же > 0 – вогнутый.

Разность ординат графика и касательной при одной и той же абсциссе x равна

или

Применяя к разности f(х) -f(х₀) формулу Лагранжа, получаем

где c заключено между х и х₀.

К разности тоже применим формулу Лагранжа, получим

, где c₁ заключено между х₀ и c, а, следовательно, между х₀ и х. По условию (x)< 0 в интервале (а; b),значит (c₁)< 0. Разности х- х₀ и c – х₀ одного знака, так как c заключено между х₀ и х, значит (х- х₀)(c – х₀)> 0.

Поэтому у – У < 0 или у <У. Мы доказали, что для любой точки x интервала (а_, b) ордината касательной больше ординаты графика, то есть график выпуклый. Аналогично доказывается, что при > 0 график вогнутый.

Асимптоты графика функции

Асимптотой графика функции у = f(x) называется прямая, расстояние от которой до текущей точки графика функции стремится к нулю при неограниченном удалении этой точки от начала координат.

Для нахождения вертикальных асимптот, то есть асимптот, параллельных оси OY, надо найти точки разрыва функции II рода. Если х₀ – такая точка, то хотя бы один из пределов f(x) или f(x) равен бесконечности. Это означает, что прямая х = х₀ – вертикальная асимптота. Если функция не имеет точек разрыва II рода, то график функции не имеет вертикальных асимптот.

Пусть график функции y = f(x) имеет невертикальную асимптоту. Уравнение невертикальной прямой можно записать в виде y = kx+b. Пусть М(х,у) – текущая точка графика. Опустим из точки М перпендикуляр МN на асимптоту. Из определения асимптоты следует: MN = 0. Из ∆М₁ MN получаем М₁М = , где  – угол между асимптотой и осью ОХ. Поскольку  – величина постоянная, то . Заметим, чтоМ₁М = РМ₁-РМ = у_{асимпт.}-у_{графика} = (kx+b)-f(x), поэтому Последнее равенство означает, что функцияявляется бесконечно малой при. Разделим обе части последнего равенства нах и перейдем к пределу при , получим. Так как

Определим теперь b. Так как тоПереходя к пределу при, получаем

19. Общая схема исследования функций. Исследование графиков.

План исследования функции и построение графика

Исследование функции удобно проводить по следующему плану.

1. Область определения функции.

2. Точки пересечения графика функции с осями координат.

3. Четность, нечетность функции.

4. Исследование функции на непрерывность. Вертикальные асимптоты.

5. Невертикальные асимптоты.

6. Интервалы монотонности. Экстремумы.

7. Интервалы выпуклости, вогнутости. Точки перегиба.

8. Дополнительные точки, (по мере необходимости).

9. Построение графика.

Подчеркнем, что пункт 8 не является необходимым. его выполняют, если необходимо уточнить график.

 

Пример 1. Исследовать функцию и построить ее график.

1. Область определения ().

2. Пусть х=0, тогда у=0. Пусть у=0, тогда и. Итак, (0;0) и– точки пересечение графика с осями координат.

3. у(-х) =  – функция не является ни четной, ни нечетной.

4. Функция непрерывна во всей области определения. Вертикальных асимптот нет.

5. Невертикальные асимптоты

Найдем k и b, если они существуют. поэтому приневертикальной асимптоты не существует. Аналогично можно показать, что и приневертикальных асимптот не существует.

6. Вычислим Найдем критические точки: х = 1 – критическая точка. Кроме того, y' не существует при х = 0 – тоже критическая точка. Нанесем критические точки на числовую прямую и определим знаки производной в образовавшихся интервалах.

Таким образом, на интервалах (-и (1;+функция возрастает, на интервале (0;1) убывает.

у_max = f(0) = 0, y_min = f(1)= -1.

7. Вычислим

у'' не обращается в нуль ни при каком значении х и у'' не существует при х=0. х=0 – критическая точка второго порядка. Нанесем критическую точку на числовую прямую и определим знаки второй производной в образовавшихся интервалах.

Таким образом, на интервалах (играфик функции вогнутый, точек перегиба нет.

8. Заметим, что , то есть в точке (0;0) график имеет вертикальную касательную.

20. Определение неопределённого интеграла и его свойства.

Дадим строгое математическое определение понятия неопределенного интеграла.

Выражение вида называетсяинтегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом всегда присутствуетdx.

Определение. Неопределенным интегралом называется функцияF(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. илиФункциюназываютпервообразной функции . Первообразная функцииопределяется с точностью до постоянной величины.

Напомним, что -дифференциал функции и определяется следующим образом:

Задача нахождения неопределенного интеграла заключается в нахождении такой функции, производная которой равняется подынтегральному выражению. Данная функция определяется с точностью до постоянной, т.к. производная от постоянной равняется нулю.

Например, известно, что , тогда получается, что, здесь- произвольная постоянная.