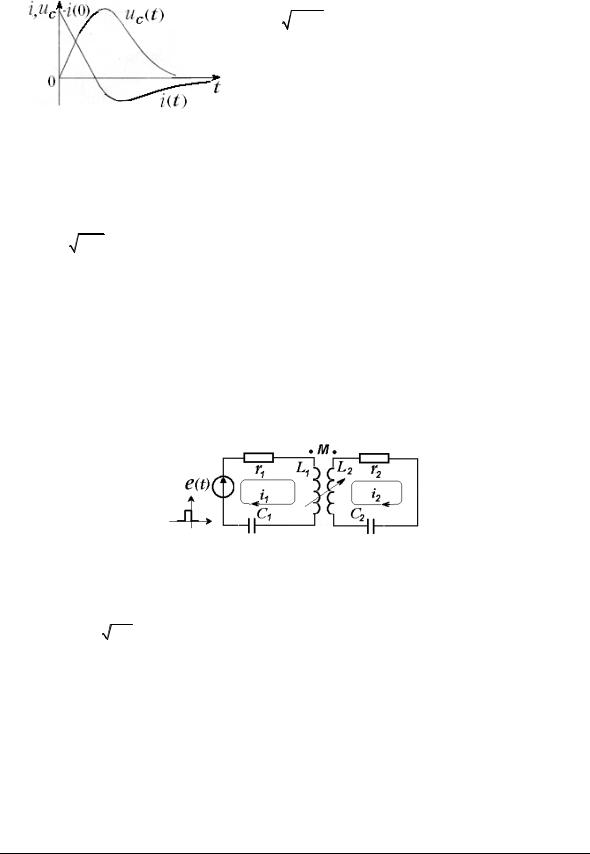
конденсаторе: WC =CuC2 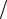2 . Этот процесс сопровождается неизбежными потерями в резисторе и постепенно вся электромагнитная энергия переходит в тепловую.

Апериодический режим

Рис. 4. Графики тока контура и напряжения на емкости в случае апериодического режима

Критический режим

Пусть параметры контура таковы, что α > ω0 (или r > 2 L / C ). В этом случае β — вещественная

величина и α > β. Из (2), а также из рис. 4 видно, что колебаний в контуре нет, а функции для напряжения uC(t) и тока i(t) — апериодические (нециклические, неколебательные). Это объясняется тем, что из-за большого значения сопротивления потерь вся электромагнитная энергия достаточно быстро (в течение короткого промежутка времени) преобразуется в тепловую.

Рассмотрим критический режим, понимая в качестве такого — переход от апериодического режима к колебательному. Он реализуется при следующих значениях параметров: α=ω0, β=0, r = 2 L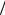C . Стоит обратить внимание, что при этом добротность контура Q = 1/2, а затухание d = 2. Для напряжения на емкости получаем:

uC (t) = (i(0)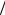C)te−αt . (5)

Чтобы реализовать критический режим, можно, наблюдая осциллограммы uC(t), увеличивать сопротивление rдоб добавочного резистора (см. рис. 1) до значения, при котором визуально фиксируется переход от колебательного режима к апериодическому.

Система связанных контуров

Рассмотрим режим свободных колебаний в колебательной системе с двумя степенями свободы. Таковой является электрическая цепь, представляющая собой систему двух индуктивно связанных колебательных контуров (рис. 5).

Рис. 5. Система двух индуктивно связанных контуров

Связь контуров с одинаковыми резонансными частотами

Будем для простоты считать, что контуры не имеют потерь (r1 = r2 = 0) и построены из одинаковых элементов: L2=L1=L, C2=C1=C. Резонансные частоты этих контуров одинаковы и

равны ω0 =1/ LC . Связь между контурами количественно характеризуется значением взаимной индуктивности М.

Пусть, как и ранее, в короткий интервал времени, длящийся до момента времени t = 0, система подвергается ударному возбуждению импульсом ЭДС, которая вводится в первый контур (см. рис. 5). Используя второй закон Кирхгофа, можем записать следующую систему уравнений для токов при t ≥ 0:

	di			1			∫i1dt + M	di
L	1	+						2
	dt			C					dt
	di2					1			di1
L			+				∫i2dt + M
	dt				C				dt

= 0

. (6)

= 0

Исследование свободных колебаний в контурах

стр.5

Решение этой системы уравнений, полученное при некотором начальном значении тока в первом контуре (i1(0)≠0) и нулевом токе во втором (i2(0)=0) имеет вид:

i (t) =	i1(0)			(cos(Ω t) + cos(Ω			2	t)) = i(0) cos(Ω1	−Ω2	t) cos(Ω1 + Ω2 t),
1	2			1					2	2	(7)
		i1(0)				t) − cos(Ω t)) = i(0)sin(Ω1			− Ω2	t)sin(Ω1 + Ω2 t).
i (t) =				(cos(Ω	2
2	2						1		2	2

Здесь символами Ω1 и Ω2 обозначены частоты связи. Они вводятся формулами:

Ω =	ω0		, Ω	2	=	ω0		, k = M / L .
1	1	−k			1		+ k

Коэффициент k = M /L называют коэффициентом связи.

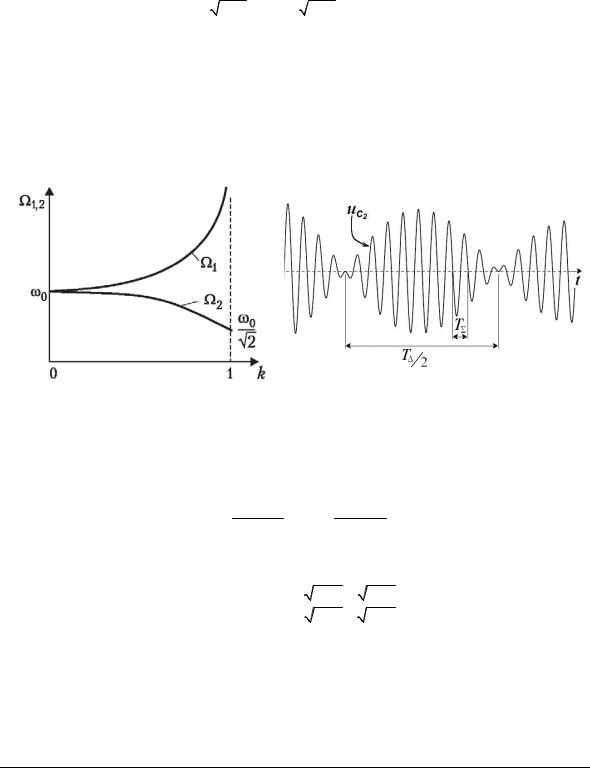
Из (7) видно, что свободные колебания в двухконтурной цепи складываются из двух колебаний с разными частотами — именно разными, хотя контуры совершенно одинаковы. Причиной «расщепления» частоты ω0 на две — быструю (Ω1) и медленную (Ω2) — является связь между контурами, поэтому частоты свободных колебаний, возникающих в связанных контурах, называют частотами связи. Их можно измерить, подключив к системе волномер — измерительный прибор, избирательно реагирующий на колебание, частота которого совпадает с частотой настройки контура волномера. Графики зависимостей частот связи от коэффициента связи k показаны на рис. 6.

Рис. 6. Графики зависимостей частот связи	Рис. 7. Осциллограмма напряжения на емкости
от коэффициента связи	второго контура

Вместе с тем, формулы (7) при близких значениях Ω1 и Ω2 (случай слабой связи) указывают на наличие биений (рис. 7). Действительно, множитель, зависящий от низкой (разностной) частоты, уместно трактовать как огибающую колебаний высокой (суммарной) частоты. Период огибающей и период высокочастотного заполнения будут равны соответственно:

T = Ω14−πΩ2 , TΣ = Ω14+πΩ2 .

Осциллограммами напряжений на емкостях контура можно воспользоваться для измерения коэффициента связи k. Отношение периода огибающей к периоду высокой частоты равно:

	N =	T	=	Ω1 + Ω2	=	1 + k +	1 − k	.(8)
		TΣ		Ω1 − Ω2		1 + k −	1 − k

Из этой формулы при k<<1 вытекает приближенное соотношение: N ≈ 2/k.

Связь контуров с разными резонансными частотами

До сих пор рассматривались контуры с одинаковыми резонансными частотами. Теперь отменим это условие. Степень расстройки второго контура по отношению к первому будем характеризовать коэффициентом X, имеющим смысл относительной расстройки контуров:

X = ω02 / ω01 = f02 / f01 .

Исследование свободных колебаний в контурах

стр.6

Анализ свободных колебаний в двухконтурной системе при расстройке второго контура относительно первого довольно громоздок. Ограничимся здесь только описанием зависимостей относительных частот связи от относительной расстройки X при разных значениях коэффициента связи k. Потери в контурах по-прежнему считаем малыми.

Итак, относительные (по отношению к ω01) частоты связи свободных колебаний в связанных контурах равны:

Ω1,2			+ X	2	±	(1+ X	2	)	2		−4(1−k		2	) X	2 12
	=	1														.
ω										2
						2(1−k						)
01

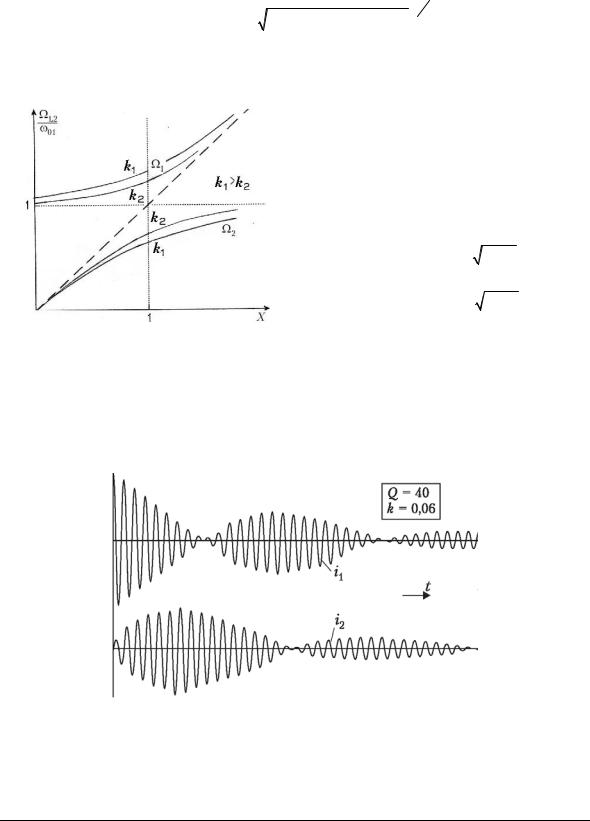
Графики этих зависимостей, называемые графиками Вина, изображены на рис. 8. Из них видно, что с увеличением связи между контурами увеличивается расхождение частот связи.

Таким образом, в связанных контурах возникают колебания токов и напряжений на двух частотах Ω1 и Ω2. И по виду они подобны амплитудно-модулированным колебаниям. При больших расстройках ( X 1 и X 1 ) относительные частоты связи асимптотически стремятся к следующим значениям:

при

X 1

имеем:

Ω1

→

X

,

Ω2

→1;

ω

1−k

2

ω

01

01

при

X 1

имеем:

Ω1

→

1

,

Ω2

→0.

ω

1−k

2

ω

01

01

С энергетической точки зрения собственные Рис. 8. Графики Вина колебания в системе связанных контуров

характеризуются перераспределением энергии между индуктивным и емкостным накопителями. Этот процесс происходит с высокой (быстрой) частотой. С другой стороны, энергия циклически «перекачивается» между первым и вторым контурами, и происходит это с разностной (медленной) частотой. Свободные колебания сопровождаются неизбежными потерями в резисторах, и поэтому со временем колебания затухают. Осциллограммы токов и напряжений двухконтурной системы, обладающей энергетическими потерями, представляют собой затухающие колебания с биениями (рис. 9).

Рис. 9. Временные характеристики для токов в контурах с учетом потерь

В заключение отметим, что рассмотренная двухконтурная система является типичным примером связанной системы с двумя степенями свободы. Аналогичные процессы наблюдаются в механических (две струны), сверхвысокочастотных и оптических колебательных системах.

Исследование свободных колебаний в контурах

стр.7