А.Н.Евграфов, Г.Н.Петров. Теория механизмов и машин. Лекция 3.

Глава 2. Геометрия и кинематика механизмов

1. Геометрический анализ механизмов

Пусть задан некоторый механизм (рис. 2.1): его структура и размеры звеньев, а также входная обобщенная координата q. Целью геометрического анализа является определение зависимостей выходных параметров (например, углов поворота ₂ и ₃ звеньев 2 и 3 или координат некоторой точки К) от координаты q. Зависимость выходных параметров от входных обобщенных координат механизма называется функцией положения механизма.

Д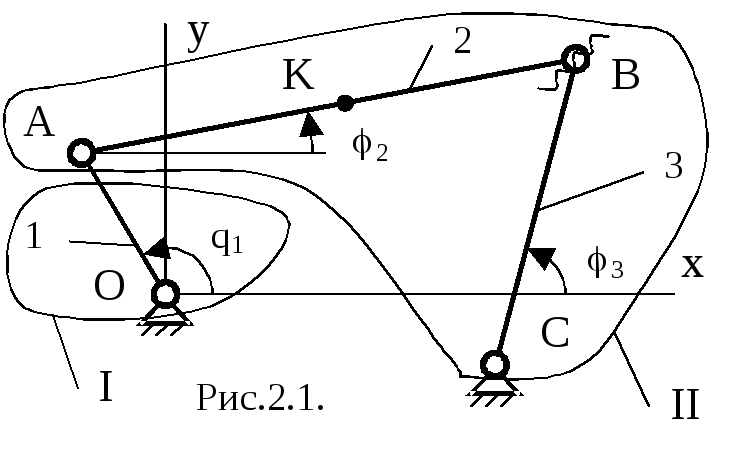ля механизма, показанного на рис. 2.1, функции положения могут быть записаны в общем виде:

(2.1)

Определение функций положения механизма составляет прямую задачу геометрического анализа. Если известен закон изменения входной координаты q₁(t), то, решив прямую задачу, можно найти законы изменения выходных параметров х_К(t)=П_Хк[q₁(t)], y_K(t)=П_Yk[q₁(t)] и т.д. Рассмотрим последовательность составления функции положения.

1. Проводится структурный анализ механизма. В шарнирном четырехзвеннике, как уже отмечалось, можно выделить однозвенную одноподвижную группу I, включающую в себя кривошип 1 и вращательную пару 0, и группу Ассура II типа ВВВ, содержащую звенья 2 и 3 и три вращательные пары А, В и С.

2. В каждой структурной группе вводятся входные и выходные координаты. Входными координатами группы являются входные обобщенные координаты механизма, попавшие в данную группу (например, координата q₁ в группе I на рис. 2.1), и координаты, определяющие положение кинематических пар предыдущих групп, к которым присоединяется рассматриваемая группа (например, для группы II на рис. 2.1 это координаты точек А и С: х_А, у_А, х_С, у_С).

Выходные координаты группы– координаты, определяющие положение кинематических пар, к которым присоединяются последующие группы, а также выходные координаты механизма (для группыIна рис. 2.1 это координаты точки А: х_А, у_А, для группыIIэто, например, координаты точки К: х_К, у_К.

3. Путем размыкания некоторых кинематических пар структурные группы приводят к открытым кинематическим цепям типа «дерево». Группа Iна рис. 2.1, присоединенная к стойке, уже образует структуру «дерева», поэтому в ней ничего размыкать не надо. В группеIIразмыкание можно провести, например, в шарнире В. Тогда, присоединив звено 3 к стойке или звено 2 к группеI, мы получим открытые кинематические цепи типа «дерево». При размыкании кинематических пар происходит размыкание связей; в частности, в плоских механизмах в одноподвижных парах размыкаются две связи, а в двухподвижных – одна. Таким образом, при размыкании шарнира В размыкаются две связи (х_В, у_В).

4. Вводятся групповые координаты, определяющие, вместе с входными, положение звеньев «дерева». На рис. 2.1 это углы₂и₃.

5. Составляются условия замыкания ранее разомкнутых связей и функции положения. Например, координаты точки В, принадлежащей звену 2, должны быть равны координатам точки В, принадлежащей звену 3: х_В2=х_В3, у_В2=у_В3. На основе этих условий получаютсягрупповые уравнения, связывающие входные, выходные и групповые координаты структурной группы.

Введем обозначение: l₁,l₂,l₃– длины звеньев 1, 2 и 3. Тогда получим следующие соотношения для механизма на рис. 2.1.

Функции положения для группы I:

(2.2)

Групповые уравнения для группы II:

(2.3)

Функции положения группы II:

(2.3’)

Уравнения (2.3) получены из условия замыкания связей в шарнире В.

Уравнения (2.2) можно назвать функцией положения точки А. В этих уравнениях известны длина l₁и входная обобщенная координатаq₁; неизвестными являются координаты точки А. Таким образом, функция положения точки А получена в явном виде. К сожалению, это удается сделать только для некоторых самых простых механизмов и структурных групп. В уравнениях (2.3) заданными являются размеры звеньевl₂иl₃и координаты точек А и С; неизвестными являются выходные координаты₂и₃; следовательно, уравнения (2.3) – это функции положения звеньев 2 и 3, полученные в неявном виде.

Если механизм обладает не одной, а Wстепенями подвижности, то входных обобщенных координат у него такжеW:q₁,q₂, …q_W. Функции положения записываются в виде:

s=1, …,m, (2.4)

где m– число выходных координат.

Рассмотрим составление функций положения на примере плоской платформы (рис. 2.2). В лекции 2 было установлено, что число степеней подвижности платформы равно 3, следовательно, надо задать три входные обобщенные координаты: q₁,q₂,q₃. Если это сделать так, как показано на рис. 2.2, то механизм распадается на три структурные группы: однозвенные одноподвижныеIиIIи трехзвенную одноподвижнуюIII. Введем входные и выходные координаты.

Г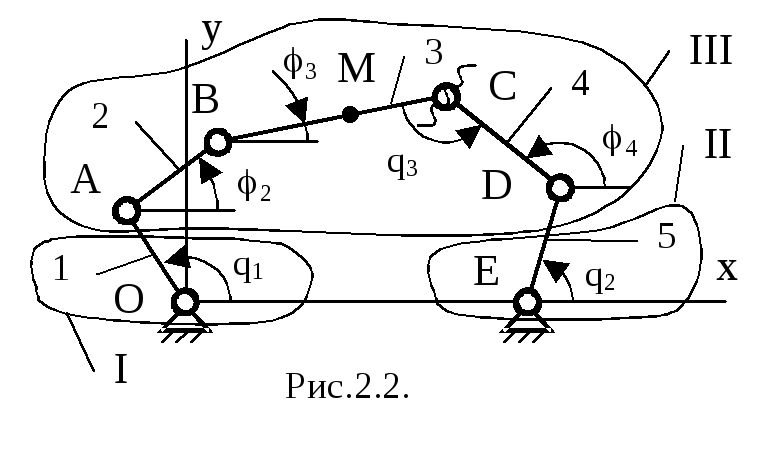руппаI: входные координаты х₀, у₀,q₁, выходные координаты х_А, у_А;

Группа II: входные координаты х_Е, у_Е,q₂, выходные координатыx_D,y_D;

Группа III: входные координаты х_А, у_А, х_D, y_D, q₃, выходные координаты х_М, у_М,₃.

Произведем размыкание группы III в шарнире C и введем групповые координаты: ₂,₃, и₄. Запишем условия замыкания: x_C3=x_C4, у_C3=y_C4. Далее составим групповые уравнения:

Группа I:

Группа II:

Группа III:(2.5)

Дополнительное уравнение для углов получим из рис. 2.2:

₃+q₃=₄. (2.6)

Часто в инженерной практике закон движения выходного звена уже задан в техническом задании; требуется определить закон изменения входных координат. Это вынуждает решать обратную задачугеометрического анализа: определение обобщенных входных координат в зависимости от выходных, т.е. отыскание функций:

q_к=Ф_к(х₁,…, х_m), к=1,…,W. (2.7)

Если число выходных координат mравно числу степеней подвижностиW, то задача может иметь одно или несколько дискретных значений, т.е. функции Ф_ксуществуют как однозначные или многозначные. Еслиm>W, то задача в общем случае не имеет решения; приm<Wнекоторое число координат (а именноW-m) можно задать произвольно.

Рассмотрим решение обратной задачи геометрии на примере трехподвижной платформы. Заданными являются все размеры звеньев и выходные координаты: х_М, у_М,₃. Надо определить входные обобщенные координатыq₁,q₂,q₃. Применим структурную инверсию, т.е. входными координатами будем считать х_М, у_М,_3,а выходными координатами -q₁,q₂,q₃(рис. 2.3). В этом случае, как отмечалось в лекции 2, механизм разбивается на три группы:I– однозвенная трехподвижная,IIиIII– двухзвенные группы Ассура типа ВВВ.

Составим уравнения для группы I:

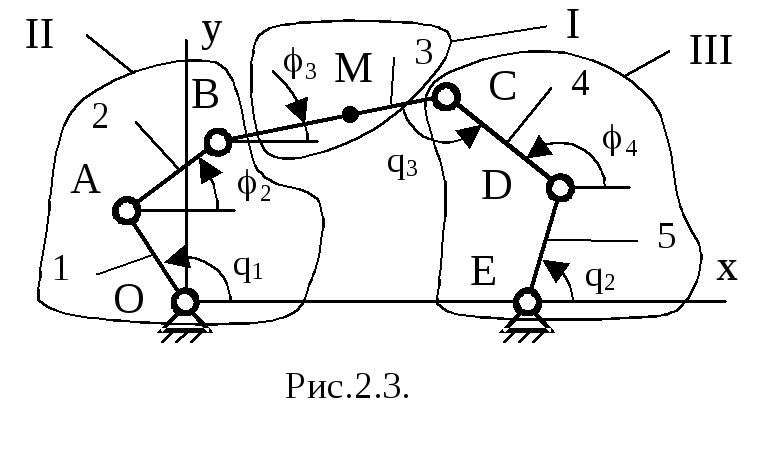
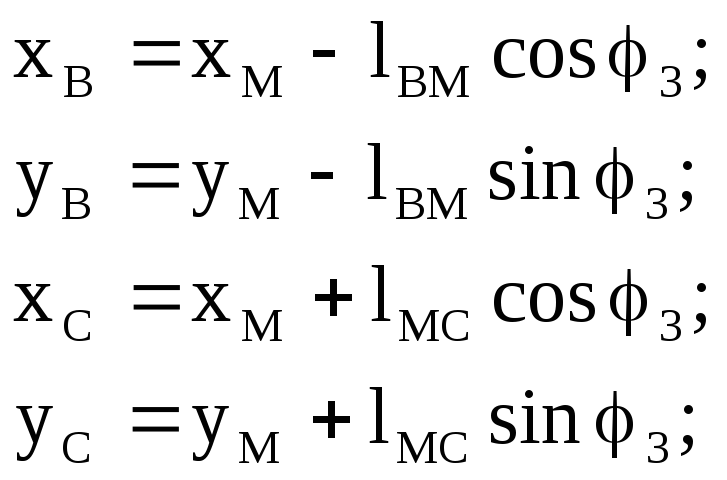(2.8)

Для группы II:

(2.9)

Для группы III:

(2.10)

Дополнительное уравнение для углов:

₃+q₃=₄.