Стандартные математические функции.

Функция	Наименование	Тип аргументов	Тип результата
sin(x)	синус x	(long)double	(long)double
cos(x)	косинус x	(long)double	(long)double
tan(x)	тангенс x	(long)double	(long)double
asin(x)	арксинус x	(long)double	(long)double
acos(x)	арккосинус x	(long)double	(long)double
atan(x)	арктангенс x	(long)double	(long)double
exp(x)	экспонента x	(long)double	(long)double
log(x)	натуральный логарифм x	(long)double	(long)double
log10(x)	десятичный логарифм x	(long)double	(long)double
pow(x,y)	x в степени y	(long)double, double	(long)double
sqrt(x)	квадратный корень из x	(long)double	(long)double
abs(x)	абсолютное значение x	int	int
fabs(x)	абсолютное значение x	(long)double	(long)double

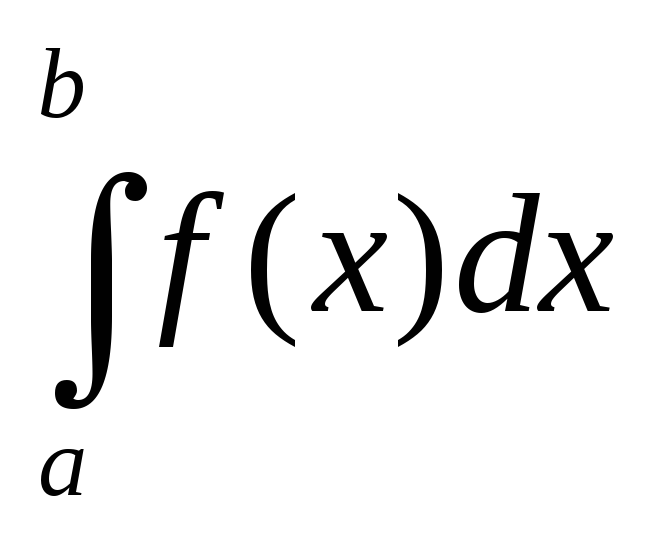
Вычисление значения с заданной точностью методом прямоугольников.

Для вычисления первого приближения интеграла разделим отрезок [a, b] на n равных частей (n=4), определим значения x _i = a + h _i – h / 2; h = ( b – a ) / n.

Вычислим площадь S _i = h * f ( x _i ). Сумма S _i площадей этих прямоугольников является приближенным значением интеграла:

Однако одно приближение не позволяет оценить точность, с которой вычислено значение интеграла, необходимо найти второе приближение. Для этого увеличим n в два раза, то есть n=2n. Аналогично S₁ найдем S₂:

Требуется вычислить значение интеграла с точностью , поэтому проверим условие |S₁-S₂|<. Если условие выполняется, то S₂ принимается за искомое значение интеграла; если не выполняется, то последнее выполненное значение S₂ считается предыдущим, то есть S₁= S₂. После этого удвоим число точек деления отрезка и вычислим новое значение S₂. Процесс удвоение n и вычисление S₂ будем продолжать до тех пор, пока модуль разности S₁ и S₂ не станет меньше .

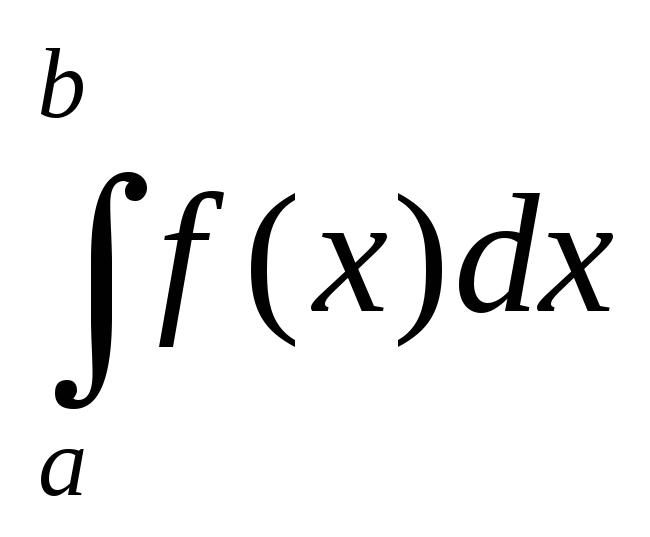
Вычисление по формуле Симпсона.

Вычисление интеграла по формуле Симпсона определяется путем деления отрезка [ a, b ] на множество более мелких отрезков.

Формула Симпсона имеет вид:

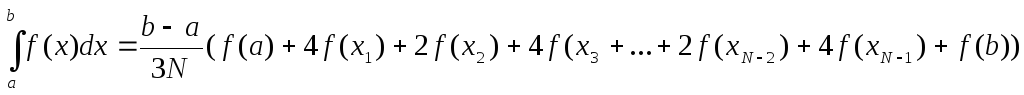
Здесь N – четное число делений интервала интегрирования: x _i = a + i ( b – a ) / N.

Алгоритм состоит в циклическом выполнении расчетов f ( x _i ). При этом следует отдельно рассмотреть случаи для границ интегрирования f ( a ) и f ( b ) и учесть, что при нечетном номере вычисляемого элемента, значение функции умножается на 4, при четном – на 2. При конечных значениях отрезка умножение не производится.

Вычисление с заданной точностью  корня уравнения F(x)=0 методом итераций.

Пусть корень уравнения находится на отрезке [ a, b ].

Для использования метода итераций исходное уравнение F(x)=0 нужно привести к виду x=f(x). Если известно начальное приближение к корню х=х₁, то подставив его в правую часть уравнения х=f(x), получим новое приближение x₃=f(x₂),……..x_k+1=f(x_k).

Итерационный процесс сходится к корню уравнения, если |f ‘(x)|<1 на отрезке, содержащем корень уравнения. Если выполняется неравенство –1<f ‘(x)<0, то корень уравнения всегда находится на отрезке [x_k, x_k+1] и условие окончания итерационного процесса имеет вид неравенства |x_k+1-x_k|<.

Переход от уравнения F(х)=0 к уравнению f(х) можно осуществить следующим образом. Умножим левую и правую части уравнения F(х)=0 на произвольную константу h и добавим к обеим частям уравнения неизвестное х. Эти действия не изменяют корней уравнения:

h F(х) +х=О*h+х

h F(х) +х=х

Обозначив f(х) =h f(х) +х, перейдем к уравнению х=f(х).

Величину h желательно выбрать такой, чтобы выполнялось неравенство –1<f '(х)<0 на отрезке, содержащем корень уравнения.

Исходными данными для программы, соответствующей приведенному алгоритму, является грубое значение корня и точность вычисления. Условием выхода из итерационного процесса является неравенство |х_k+1-х_k]<, при этом искомым значением является х_k+1.

Решить уравнение f(x)=0 с заданной точностью  методом деления отрезка пополам.

Метод деления отрезка пополам заключается в следующем.. Проверяется наличие корня на отрезке [а, b]. Для этого вычисляются значения функции f(а) и f(b) . Если f(а)*f(b) > 0, то уравнение не имеет корней на заданном отрезке. Если f(а) * f(b) < 0, т. е. на концах отрезка [а, b] функция f(х) имеет противоположные знаки, то искомый корень лежит на этом отрезке. Поиск корня происходит следующим образом. Находим в точке а значение функции у₁=f(а). Затем определяем значение х как среднюю точку между а и b, вычисляем значения у₂=f(х). Теперь, если f(а) * f(х) > 0, то корень находится на отрезке [a, b]. Переместим точку а вправо, выполнив присвоение а=х. В противном случае нужно перемещать влево точку b: b=х. Таким образом получим второй отрезок [а, b], но вдвое меньше предыдущего. Процесс деления отрезка пополам продолжается до тех пор, пока отрезок [а, b] не станет меньше заданной точности.