Проектирование САУ ОМТ2

30

2.ДИНАМИКА

Ньютоновская механика, механика Эйлера и механика Лагранжа-Кирхгофа.

Уравнения нелинейной динамики движения тел с 6-ю степенями свободы (3-поступательных и 3-вращательных) имеют следующий вид [4]:

(1)

- матрица инерции (включая присоединенные массы),

- матрица кориолисовых и центростремительных сил,

- матрица демпфирующих гидродинамических сил,

- вектор гравитационных сил и моментов (включая архимедовы силы и восстанавливающие силы),

- вектор управляющих сил,

-вектор возмущающих сил (ветро-волновые возмущения).

Динамика Ньютона

Основана на втором законе Ньютона, который устанавливает связь между массой тела , ускорением и силой

.

Если сила равна 0, то тело движется с постоянной скоростью () или находится в состоянии покоя (первый закон Ньютона). Третий закон Ньютона: действие равно противодействию (раскрывает природу возникновения сил при взаимодействии тел).

Эти законы были опубликованы в 1687 Исааком Ньютоном (1643-1727) в «Философии естественных (природных) начал математики».

Первая и вторая аксиомы Эйлера

Леонард Эйлер (1707-1783) распространил существующий второй закон Ньютона в терминах линейных сил (вызывающих линейное движение) и угловых моментов (вызывающих вращательное движение) в «Новых комментариях Императорской Научной Академии Петербурга». Эти результаты известны как Первая и Вторая Аксиомы Эйлера

- силы и моменты относительно центра тяжести (масс) тела, - угловая скорость и -тензор инерции относительно центра тяжести (масс).

Эти аксиомы привели к развитию векторных форм механики.

Формулировка механики Лагранжа

Наиболее распространенным подходом является механика Лагранжа.

Этот подход включает в себя три основных шага. На первом формируются соотношения для кинетической и потенциальной энергий ОМТ. На втором вычисляется Лагранжиан :

На третьем используется уравнение Лагранжа

.

В правой части силы управления (в связанной СК) пересчитываются в неподвижную СК.

В соответствии с первым разделом вектор -обобщенные координаты, описывающие пространственное движение МПО (6 степеней свободы, ) в неподвижной СК.

Следует отметить, что альтернативное представление (параметры Эйлера) не может быть использовано в подходе Лагранжа, поскольку это представление использует 7 параметров и не может представлять обобщенные координаты.

Часто пытаются сформировать уравнения движения в связанной системе координат. К сожалению, вектор не может представлять обобщенные координаты с точки зрения позиции и ориентации. Действительно, не имеет непосредственной физической интерпретации. Соответственно, мы не можем использовать напрямую уравнения Лагранжа, чтобы вывести уравнения движения в связанной системе координат. Однако, задача может быть решена применением уравнений движения Кирхгофа или так называемым квази-Лагранжевым подходом.

Уравнения Кирхгофа (Лагранжа второго рода) в векторной форме.

(Получили наибольшее распространение в современной литературе )

Рассматривается ОМТ, вектор скорости которого,-поступательная скорость в связанной системе координат , и -угловая скорость . связаны с кинетической энергией

уравнениями

(12)

- силы управления и внешние силы

Квази - Лагранжевы уравнения движения.

Квази- Лагранжевы уравнения являются наиболее общей версией уравнений Кирхгофа, где Лагранжиан используется вместо кинетической энергии . Это позволяет учитывать гравитационные (потенциальные) силы.

Эти уравнения имеют вид:

Первые составляющие от кинетической энергии, последние (отрицательные) от потенциальной энергии. Таким образом, можно использовать уравнения Кирхгофа (Лагранжа второго рода), добавляя потенциальные силы и силы влияния среды.

Динамика твердого тела.

Для вывода уравнений динамики обычно используются уравнения Лагранжа второго рода

(13)

При этом вводится главный вектор количества движения ОМТ

и главный вектор момента количества движения

.

В этом случае уравнения Лагранжа примут вид

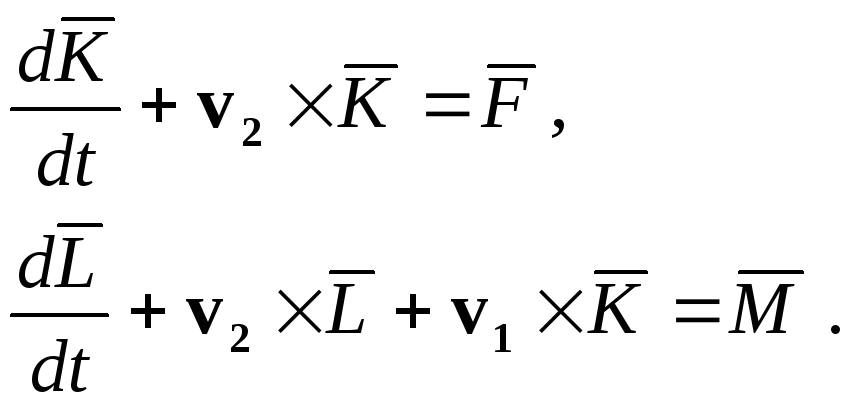
Векторы имеют вид

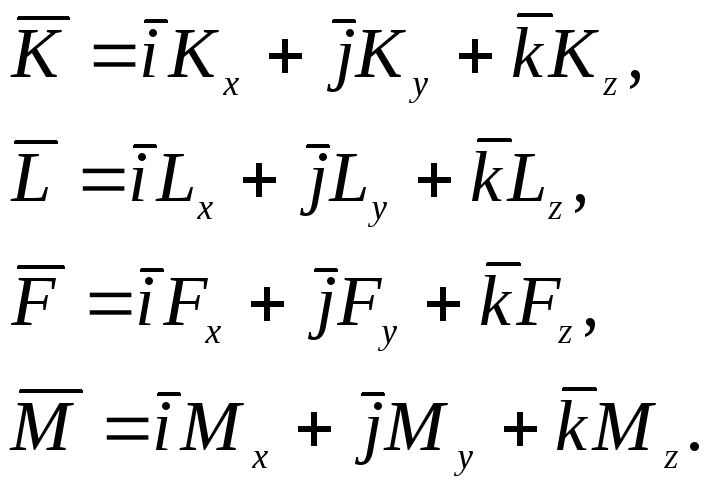
Векторные произведения вычисляются через определители с последующим разложением по элементам первой строки.

Тогда имеем

(14)

(15)

(16)

Кинетическая энергия определяется выражением

, (17)

где -матрица инерции ОМТ как твердого тела(rigid body), -матрица инерции присоединенных (added) масс жидкости, которая зависит от вида движения(поступательное,вращательное,поступательно-вращательное).

, (18)

-массовая плотность тела, -элементарный объем.

Если начало связанной системы находится в центре масс ОМТ () и координатные оси являются главными центральными осями инерции (), то матрица превращается в диагональную.

Уравнения движения твердого тела (без присоединенных масс)

Определим (вектор Ньютоновых и Кориолисовых сил).

(19)

Используем уравнения Лагранжа второго рода

Кинетическая энергия в общем случае из(18,19)

Из уравнения Лагранжа следует

;

Матрица кориолисовых и центростремительных сил

.

Учет присоединенных масс жидкости (инерционные гидродинамические силы)

Кинетическая энергия жидкости вовлекаемой в движение

По аналогии с матрицей инерции твердого тела

;

Для твердого тела в состоянии покоя и без внешних воздействий присоединенная матрица инерции положительно определенная .

Кинетическая энергия

Силы и моменты присоединенных масс

Уравнения Лагранжа 2-го рода (Кирхгофа) имеют вид

;

;

;

;

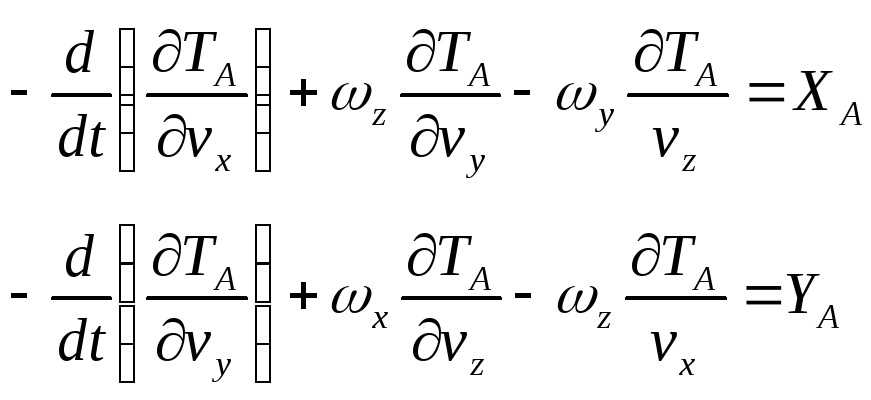
- ньютоновы и кориолисовы силы вызванные присоединенными массами (по аналогии с твердым телом)

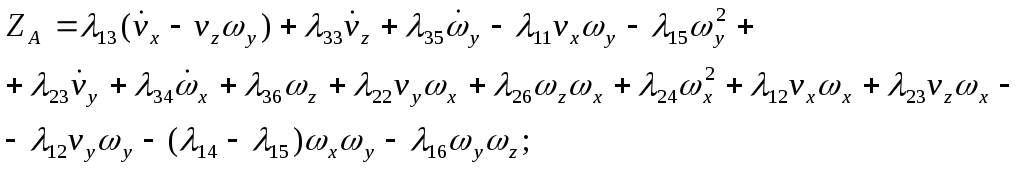
Силы, включающие производные координат относятся к ньютоновым, остальные к кориолисовым и центростремительным.

Матрица кориолисовых и центростремительных сил от присоединенных масс жидкости

По аналогии с матрицей для твердого тела

, (20)

где

Примеры сил от присоединенных масс:

- для надводных кораблей

Движение на плоскости 0xz и вращательное движение относительно 0у

.

- для подводных аппаратов (обладают симметрией)

.

Метод плоских сечений для вычисления присоединенных масс.

МПО разбивается вдоль длины на секции. Для каждой секции (двумерная площадь) вычисляются присоединенные массы, которые затем суммируются по всей длине МПО.

Для погруженного (и тонкого ) подводного МПО, длиной , мы можем использовать следующие формулы [4]

Для кругового сечения

, -радиус сечения;

Для сечения в виде эллипса

, -полуоси эллипса,

Для квадратного сечения

, -сторона квадрата.

Для двумерных присоединенных моментов инерции

-длина,-высота, -ширина (главные размерения ОМТ).

График зависимости присоединенных масс для прямоугольного сечения приведен на рис.7 ниже

Рис.7

Для надводного корабля мы можем использовать аппроксимацию и , представив подводную часть корабля полуцилиндром с присоединенной массой

,

-радиус цилиндра (при постоянном принимается ), -плотность воды. Аналогично следующий ряд соотношений можно использовать

Присоединенные массы для тел эллипсоидной формы

По счастью многие присоединенные массы в общем выражении равны нулю, когда тело обладает какой-либо симметрией. Рассмотрим эллипсоид полностью погруженный в воду с полуосями , рис.8

Рис.8

Уравнение эллипсоида

При имеем сфероид.

Имплай (1961) вывел следующие соотношения для присоединенных масс (матрица присоединенных масс является диагональной ввиду симметрии тела по всем трем плоскостям)

Масса сфероида

. Введем ,

тогда константы вычисляются как

.

Альтернативное представление сделано Ламбом (1932) с помощью коэффициентов присоединенных масс

;

;

.

Тогда присоединенные массы

Для сфероида