
pz_kodirovanie
.pdfМинистерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра математики
ЭЛЕМЕНТЫ ТЕОРИИ КОДИРОВАНИЯ Практические занятия по дисциплине Дискретная математика
Санкт-Петербург
2013 г.
1
Оглавление. |
|
3. Элементы теории кодирования |
2 |
3.1. Разделимые и неразделимые схемы алфавитного |
|
кодирования. Префиксные алфавитные коды |
3 |
3.2. Коды с минимальной избыточностью. Построение дерева |
|
Хаффмена |
5 |
3.5. Кодирование с исправлением ошибок. |
15 |
3.5.1 Построение кодов Хемминга.. Обнаружение ошибки в кодах Хем- |
|
минга. Декодирование кодов Хемминга, содержащих одну ошибку |
15 |
3.5.2. Линейные или групповые коды . Декодирование |
|
по лидеру смежного класса |
17 |
2
3.Элементы теории кодирования
3.1.Разделимые и неразделимые схемы алфавитного кодирования. Префиксные алфавитные коды
Задача 3.1. Пусть A {a1 , a2 }– алфавит сообщений, |
B {0,1} – ко- |
дирующий алфавит. Установить, является ли префиксным и взаимно одно-
значным |
алфавитный |
код |
( A) , |
заданный |
схемой |
(A) :{a1 0, a2 01}.
Вслучае однозначности декодирования по слову 000100010 восста-
новить исходное сообщение.
Решение. В данном случае код не является префиксным, так как элементарное кодовое слово 1 0 является префиксом другого элементар-
ного кодового слова 2 01. Для декодирования слова выделим в этом слове пары (01) , т.е. представим слово в виде 00(01)00(01)0 . Отсюда видно, что существует единственное слово сообщения a1a1a2 a1a1a2 a1 ,
кодовым словом которого является слово , |
т.е. декодирование является |
||
однозначным для заданной схемы, не обладающей свойством префикса. |
|||
Задача 3.2. |
Пусть |
A {a1, a2 , a3}– |
алфавит сообщений, |
B {b1,b2 ,b3} – |
кодирующий алфавит. Установить, является ли префикс- |
||
ным и взаимно однозначным |
алфавитный код ( A) , заданный схемой |
||
(A) :{a1 b1 , a2 b1b2 , a3 |
b3b1}. В случае однозначности декодиро- |
||
вания по слову |
b3b1b1b2b1b2b1b1b3b1 восстановить исходное сообще- |
||
ние. |
|
|
|
Решение. Данный код не обладает свойством префикса, так как элемен-
тарное кодовое слово |
1 |
b1 является префиксом другого элементарного |
|||
кодового слова |
2 b1b2 . |
Для декодирования слова |
выделим в этом |
||
слове пары |
( b1b2 ) |
и |
|
( b3b1 ), т.е. представим |
слово в виде |
(b3b1 )(b1b2 )(b1b2 )b1b1 (b3b1 ) . Это слово может быть однозначно декоди-
ровано словом a3a2 a1a1a3 .
Задача 3.3. Выяснить, обладает ли свойством префикса код
K {a,ba,...,b(a)n ,...}
3
префиксом элементарных кодовых слов вида b(a)n baa...a при |
n 2 . |
|
Задача 3.4. Заданы алфавит сообщений A {1,2,3,4,5} , кодирующий |
||
алфавит B {0,1,2} и схема кодирования |
является |
|
|
1 10 |
|
|
2 12 |
|
|
||
|
3 012 |
|
: |
||
|
4 101 |
|
|
|
|
Решение. Код не обладает свойством префикса, так как ba |
||
5 2100 |
|
|
|
|
|
Выяснить, являются ли слова 1 10120121012100 , 2 0121001210201 ,
3 1010122100 кодовыми словами сообщений. В случае, если являются,
найти соответствующие слова сообщений, Является ли заданная схема разделимой? Проверить выполнение неравенства Макмиллана для заданной схемы.
Решение. Данная схема кодирования не является префиксной, так как элементарное кодовое слово 1 10 является префиксом элементарного кодового слова 4 101. Поэтому схема кодирования может быть разделимой или неразделимой. Представляя заданные слова в виде
1 (10)(12)(012)(101)(2100) , 2 (012)(10)(012)(10)201,
3 (10)(10)(12)(2100) (101)(012)(2100) , получим, что 1 является ко-
довым словом и ему соответствует слово сообщения 1 12345 , 2 не
является кодовым словом, |
3 является кодовым словом, но декодируется |
||||||||||||
неоднозначно: ему соответствует два слова сообщений 3 1125 и |
|||||||||||||
~ |
435 . Следовательно, заданная схема кодирования не является раз- |
||||||||||||
3 |
|||||||||||||
делимой. |
Неравенство Макмиллана для заданной схемы выполняется: |
||||||||||||
|
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|
25 |
1 |
32 |
|
33 |
|
34 |
|
||||||||
32 |
|
33 |
|
|
81 |
||||||||
Задача 3.5. С помощью неравенства Макмиллана выяснить, может ли набор чисел (1,2,2,3) быть набором длин элементарных кодовых слов раз-
делимого кода в двоичном кодирующем алфавите.
4
Решение. Данный набор чисел не может быть набором длин элементарных кодовых слов разделимого кода в двоичном кодирующем алфавите, так
как |
1 |
|
1 |
|
1 |
|
1 |
|
9 |
1 |
|
2 |
22 |
22 |
23 |
8 |
|||||||
|
|
|
|
|
|
Задача 3.6. Пусть задан алфавитный двоичный код для алфавита сообщений A {a1 , a2 ,..., am }, длины элементарных кодовых слов не превы-
шают n : li n , при этом m 2n . Может ли этот код быть однозначно де-
кодируемым? префиксным?
Проверим выполнение неравенства Макмиллана
m |
1 |
m |
1 |
|
m |
|
|
|
|
|
1 . |
||||
l |
n |
n |
|||||
i 1 |
2 i |
i 1 |
2 |
|
2 |
|
Неравенство Макмиллана не выполняется, следовательно заданный код является неразделимым, а, значит он не может быть префиксным (префиксные коды всегда однозначно декодируемы).
3.2. Коды с минимальной избыточностью. Построение дерева Хаффмена. Построение дерева Хаффмена
Пусть задан алфавит сообщений A {a1 , a2 ,...am } и кодирующий дво-
ичный алфавит B {0,1} . Относительные частоты появления букв алфа-
вита A определяются распределением вероятностей p1 p2 ... pm ,
где p1 p2 ... pm 1. Двоичное дерево Хаффмена H m строится из букв алфавита A соответствующих вероятностей. Вершины x дерева определяются упорядоченной парой ( Ax , px ) , где Ax A , px – суммар-
ная вероятность элементов, входящих в Ax .
Дерево строится снизу вверх по направлению к корню. На первом шаге все буквы алфавита A со своими вероятностями объявляются вершинами и рассматриваются как поддеревья Ti , корнями которых являются их вер-
шины. На каждом шаге происходит слияние двух поддеревьев Ti и T j с ми-
нимальными значениями вероятностей pi и p j их корней. В результате образуется поддерево Tij с корнем, которым является новая вершина. Ей соответствует вероятность pij pi p j .У новой вершины-корня (правым)
5

поддеревом будет Ti , а правым (левым) поддеревом будет T j .Обычно
правым поддеревом назначают то, в котором больше уровней. Каждое слияние поддеревьев уменьшает их число на единицу. Слияние продолжается до тех пор, пока не будет построено одно дерево. В этом дереве корень будет представлен одним множеством A и суммарной вероятностью
p1 p2 ... pm 1.
Задача 3.7. Задан алфавит сообщений A {a,b, c, d, e, f , g, h} и кодирующий двоичный алфавит B {0,1} . Относительные частоты появления букв определяются распределением вероятностей p1 p2 ... p8 , кото-
рые имеют следующие значения 0.64, 0.12, 0.08, 0.04, 0.04, 0.04, 0.02, 0.02 .
Построить кодовое дерево Хаффмена и кодовую схему.
Решение. Будем рассматривать все буквы алфавита со своими вероятностями как вершины дерева. Обозначим их через A, B, C, D, E, F, G, H
, E, F,G, H соответственно. В таблице 3.1 приведены вершины и соответствующие им вероятности.
Таблица 3.1
A |
B |
C |
D |
E |
F |
G |
H |
|
|
|
|
|
|
|
|
0.64 |
0.12 |
0.08 |
0.04 |
0.04 |
0.04 |
0.02 |
0.02 |
|
|
|
|
|
|
|
|
1) В результате слияния двух вершин G и H с минимальными значениями
вероятностей образуется новая вершина |
GH , которой соответствует ве- |
|||||||
роятность |
p78 |
0.04 |
. Соответствующее поддерево имеет вид |
|||||
|
|
|
|
|
|
|
|
GH |
|
|
A |
B |
C |
D |
E |
F |
|
G H
Рис.3.1 2) Теперь уже в слиянии участвуют вершины, представленные в таблице 3.2
Таблица 3.2
6

|
A |
B |
C |
|
D |
E |
F |
<GH> |
|
|
|
|
|
|
|
|
|
|
|
|
0.64 |
0.12 |
0.08 |
|
0.04 |
0.04 |
0.04 |
0.04 |
|
|
|
|
|
|
|
|
|
|
|
Объединяем вершины F и |
GH |
с минимальными значениями вероятно- |
|||||||
стей и назначаем правой вершину |
GH , так как она представляет подде- |
||||||||
рево с большим числом уровней. Новой вершине  F
F  GH
GH 
 соответствует
соответствует
вероятность p678 0.08 . Новый список вершин упорядочиваем по значениям вероятностей
|
|
|
Таблица 3.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
B |
C |
F GH |
|
D |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.64 |
0.12 |
0.08 |
0.08 |
|
0.04 |
0.04 |
|
|
|
|
|
|
|
|
Построим соответствующее поддерево |
|
|
|||||
|
|
|
|
|
|||
A |
B |
C |
|
FGH |
D |
E |
|
F |
GH |
|
G H
Рис.3.2
3) Объединяем вершины D и E , получим вершину  DE
DE , упорядочиваем
, упорядочиваем
вершины по значениям вероятностей , учитывая при этом, что правее должна располагаться вершина, которая представляет поддерево с большим числом уровней
Таблица 3.4
A |
B |
C |
DE |
F GH |
|
|
|
||
|
|
|
|
|
0.64 |
0.12 |
0.08 |
0.08 |
0.08 |
|
|
|
|
|
7

Соответствующее поддерево имеет вид |
|
||||
|
|
|
DE |
|
|
A |
B |
C |
|
|
FGH |
|
|
D |
E |
F |
GH |
|
|
|
|||
G H
Рис.3.3
4) Объединяем вершины  DE
DE и
и  F
F  GH
GH 
 , получаем новую верши-
, получаем новую верши-
ну 
 DE
DE
 F
F  GH
GH 

 , упорядочиваем вершины по значениям вероятностей
, упорядочиваем вершины по значениям вероятностей
|
|
Таблица 3.5 |
|
|
|
|
|
|
|
|
|
|
A |
DE F GH |
|
B |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.64 |
0.16 |
|
0.12 |
0.08 |
|
|
|
|
|
|
Построим соответствующее поддерево |
|
|
|
||
|
|
|
|
||
A |
|
DEFGH |
|
B |
C |
|
|
|
|
|
|
|
|
FGH |
|
|
|
|
DE |
|
|
|
|
D |
E |
F |
GH |
|
|
|
|
|
|||
G H
Рис.3.4
8
5) Объединяем вершины B и C , получаем новую вершину  BC
BC  , упорядо-
, упорядо-
чиваем вершины по значениям вероятностей
|
|
|
Таблица3.6 |
|
|
|
A |
|
BC |
DE F GH |
|
|
|
|
|
||
|
0.64 |
|
0.20 |
0.16 |
|
|
|
|
|
|
|
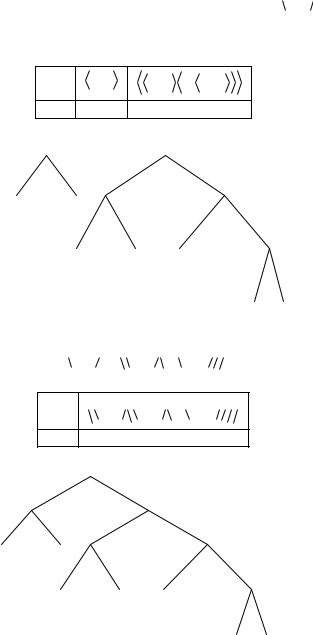
и строим соответствующее поддерево |
|
|
|||
A |
BC |
|
|
DEFGH |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
FGH |
|
B |
C |
DE |
|
|
|
|
|
|
||
|
|
D |
E |
F |
GH |
|
|
|
|||
G H
Рис.3.5
6) Объединяем вершины  BC
BC  и
и 
 DE
DE
 F
F  GH
GH 


Таблица 3.7
A 
 BC
BC 
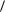
 DE
DE
 F
F  GH
GH 



0.640.36
Соответствующее поддерево имеет вид |
|
|
||
A |
|
BCDEFGH |
|
|
|
BC |
|
DEFGH |
|
|
|
|
|
|
|
|
|
|
FGH |
B |
C |
DE |
|
|
|
|
|
||
|
D |
E |
F |
GH |
|
|
|||
G H
Рис.3.6
9

7) Объединяем две последние вершины, получаем вершину
 A
A
 BC
BC 

 DE
DE
 F
F  GH
GH 



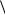 , которой соответствует вероятность p 1. В
, которой соответствует вероятность p 1. В
результате будет построено дерево Хаффмена. Пометим выходящие ребра дерева символами 0 и 1: левое ребро отметим 0, а правое отметим 1. В результате получим кодовое дерево Хаффмена. Оно представлено на рис.
3.7.
ABCDEFGH |
|
|
|
|
|
0 |
1 |
|
|
|
|
A |
|
BCDEFGH |
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
BC |
|
|
DEFGH |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0 |
1 |
|
|
|
|
|
|
FGH |
|
||
|
|
|
|
|
|
B |
C |
DE |
|
|
|
|
|
|
|
||
|
0 |
1 |
0 |
1 |
|
|
|
|
|
||
|
D |
E |
F |
|
GH |
|
|
|
|||
|
|
|
|
0 |
1 |
|
|
|
|
G |
H |
Рис.3.7
Схема алфавитного кодирования для построенного дерева Хаффмена имеет вид
|
a 0 |
|
b 100 |
|
|
|
c 101 |
|
|
d 1100: e 1101f 1110g 11110h 11111
10
