pz_grafy_

1, 2, 3, 4, 5, 6 , 1, 2, 3, 4, 6, 5 , 1, 2, 3, 5, 4, 6 , 1, 2, 3, 5, 6, 4 , 1, 2, 3, 6, 4, 5 , 1, 2, 3, 6, 5, 4 , 1, 2, 4, 3, 5, 6 , 1, 2, 4, 3, 6, 5 , 1, 2, 4, 5, 3, 6 , 1, 2, 4, 5, 6, 3 , 1, 2, 4, 6, 3, 5 , 1, 2, 4, 6, 5, 3 , 1, 2, 5, 3, 4, 6 , 1, 2, 5, 3, 6, 4 , 1, 2, 5, 4, 3, 6 , 1, 2, 5, 4, 6, 3 , 1, 2, 5, 6, 3, 4 , 1, 2, 5, 6, 4, 3 , 1, 2, 6, 3, 4, 5 , 1, 2, 6, 3, 5, 4 , 1, 2, 6, 4, 3, 5 , 1, 2, 6, 4, 5, 3 , 1, 2, 6, 5, 3, 4 , 1, 2, 6, 5, 4, 3 , 1, 3, 2, 4, 5, 6 , 1, 3, 2, 4, 6, 5 , 1, 3, 2, 5, 4, 6 , 1, 3, 2, 5, 6, 4 , 1, 3, 2, 6, 4, 5 , 1, 3, 2, 6, 5, 4 , 1, 3, 4, 2, 5, 6 , 1, 3, 4, 2, 6, 5 , 1, 3, 4, 5, 2, 6 , 1, 3, 4, 5, 6, 2 , 1, 3, 4, 6, 5, 2 , 1, 3, 4, 6, 2, 5 , 1, 3, 5, 2, 4, 6 , 1, 3, 5, 2, 6, 4 , 1, 3, 5, 4, 2, 6 , 1, 3, 5, 4, 6, 2 , 1, 3, 5, 6, 4, 2 , 1, 3, 5, 6, 2, 4 , 1, 3, 6, 4, 2, 5 , 1, 3, 6, 4, 5, 2 , 1, 3, 6, 5, 2, 4 , 1, 3, 6, 5, 4, 2 , 1, 3, 6, 2, 4, 5 , 1, 3, 6, 2, 5, 4 , 1, 4, 2, 3, 5, 6 , 1, 4, 2, 3, 6, 5 , 1, 4, 2, 5, 3, 6 , 1, 4, 2, 5, 6, 3 , 1, 4, 2, 6, 3, 5 , 1, 4, 2, 6, 5, 3 , 1, 4, 3, 2, 5, 6 , 1, 4, 3, 2, 6, 5 , 1, 4, 3, 5, 2, 6 , 1, 4, 3, 5, 6, 2 , 1, 4, 3, 6, 5, 2 , 1, 4, 3, 6, 2, 5 , 1, 4, 5, 2, 3, 6 , 1, 4, 5, 2, 6, 3 , 1, 4, 5, 3, 2, 6 , 1, 4, 5, 3, 6, 2 , 1, 4, 5, 6, 3, 2 , 1, 4, 5, 6, 2, 3 , 1, 4, 6, 3, 2, 5 , 1, 4, 6, 3, 5, 2 , 1, 4, 6, 5, 2, 3 , 1, 4, 6, 5, 3, 2 , 1, 4, 6, 2, 3, 5 , 1, 4, 6, 2, 5, 3 ,

1, 6, 3, 2, 4, 5 , 1, 6, 3, 2, 5, 4 , 1, 6, 3, 4, 2, 5 , 1, 6, 3, 4, 5, 2 , 1, 6, 3, 5, 2, 4 , 1, 6, 3, 5, 4, 2 , 1, 6, 4, 2, 3, 5 , 1, 6, 4, 2, 5, 3 , 1, 6, 4, 3, 2, 5 , 1, 6, 4, 3, 5, 2 , 1, 6, 4, 5, 2, 3 , 1, 6, 4, 5, 3, 2 , 1, 6, 5, 2, 3, 4 , 1, 6, 5, 2, 4, 3 , 1, 6, 5, 3, 2, 4 , 1, 6, 5, 3, 4, 2 , 1, 6, 5, 4, 2, 3 , 1, 6, 5, 4, 3, 2 , 1, 6, 2, 3, 4, 5 , 1, 6, 2, 3, 5, 4 , 1, 6, 2, 4, 3, 5 , 1, 6, 2, 4, 5, 3 , 1, 6, 2, 5, 3, 4 , 1, 6, 2, 5, 4, 3 ,

31

1, 5, 2, 3, 4, 6 ,		1, 5, 2, 3, 6, 4 ,		1, 5, 2, 4, 3, 6 ,
1, 5, 2, 4, 6, 3 ,		1, 5, 2, 6, 3, 4 ,		1, 5, 2, 6, 4, 3 ,
1, 5, 3, 2, 4, 6 ,		1, 5, 3, 2, 6, 4 ,		1, 5, 3, 4, 2, 6 ,
1, 5, 3, 4, 6, 2 ,		1, 5, 3, 6, 4, 2 ,		1, 5, 3, 6, 2, 4 ,
1, 5, 4, 2, 3, 6	,	1, 5, 4, 2, 6, 3	,	1, 5, 4, 3, 2, 6	,
1, 5, 4, 3, 6, 2	,	1, 5, 4, 6, 3, 2	,	1, 5, 4, 6, 2, 3	,
1, 5, 6, 3, 2, 4	,	1, 5, 6, 3, 4, 2	,	1, 5, 6, 4, 2, 3	,
1, 5, 6, 4, 3, 2	,	1, 5, 6, 2, 3, 4	,	1, 5, 6, 2, 4, 3

Для матрицы весов
1			13		7	5	2	9
2		8			4	7	5
3		8	4			3	6	2
W 4 5			8	1			0	1
5			6		1	4		9
6			0		8	3	7
	10

найдем минимальные элементы строк

242

a 010

Вычтем эти элементы из каждой строки, в результате получим матрицу

			11	5	3	0	7
		4		0	3	1
~		6	2		1	4	0
W
	5		8	1		0	1
			5	0	3		8
			0	8	3	7
	10

~

Для матрицы W найдем минимальный элемент в каждом столбце

32

h 14 .

b (4,0,0,1,0,0) . Вычитая эти элементы из соответствующих столбцов мат-

~

рицы W , получим матрицу

			11	5	2		7
						0
	0			0	2	1
		2	2		0	4	0
	W *
	1		8	1		0	1
			5	0	2		8
		6	0		2	7

Суммируя минимальные элементы строк и столбцов, получим нижнюю оценку для веса гамильтонова цикла

Минимальным элементом первой строки матрицы весов W является

w15 2 . Поэтому все множество гамильтоновых циклов, представленное таблицей, разобьем на 2 множества (1,5) A и (1){5} .При этом

(1,5) A={

1, 5, 2, 3, 4, 6 ,		1, 5, 2, 3, 6, 4 ,		1, 5, 2, 4, 3, 6 ,
1, 5, 2, 4, 6, 3 ,		1, 5, 2, 6, 3, 4 ,		1, 5, 2, 6, 4, 3 ,
1, 5, 3, 2, 4, 6 ,		1, 5, 3, 2, 6, 4 ,		1, 5, 3, 4, 2, 6 ,
1, 5, 3, 4, 6, 2 ,		1, 5, 3, 6, 4, 2 ,		1, 5, 3, 6, 2, 4 ,
1, 5, 4, 2, 3, 6	,	1, 5, 4, 2, 6, 3	,	1, 5, 4, 3, 2, 6	,
1, 5, 4, 3, 6, 2	,	1, 5, 4, 6, 3, 2	,	1, 5, 4, 6, 2, 3	,
1, 5, 6, 3, 2, 4	,	1, 5, 6, 3, 4, 2	,	1, 5, 6, 4, 2, 3	,
1, 5, 6, 4, 3, 2	,	1, 5, 6, 2, 3, 4	,	1, 5, 6, 2, 4, 3

Рассмотрим вначале множество (1,5) A.

Из графа G получим граф G' отождествлением вершин 1 и 5. Новую вершину обозначим через x . Из матрицы весов при этом удаляются первая строка и пятый столбец, пятая строка становится первой. Эти строки и столбцы выделены в матрице. Построим новую матрицу весов для графа G' , а также столбец a из минимальных элементов строк и строку b из минимальных элементов столбцов этой матрицы

33

x 5				0	2	8		0
2		0	0		2			0
W ' 3		2	2		0	0	a'	0		b' (0,0,0,0,0) .
4 1			8	1		1		1
6		6	0	8	2			0

В результате вычитания элементов a' из соответствующих строк матрицы W ' и элементов b' из соответствующих столбцов преобразованной матрицы, получим

x			5	0	2	8
2		0		0	2				~
~		2	2		0	0	и W '	*
W ' 3									W '
4	0		7	0		0
6		6	0	8	2

В результате получим оценку h1 h h' 14 1 15.

Рассмотрим теперь множество гамильтоновых циклов (1){5} , в которых вершина 1 не связана с вершиной 5, т.е. w*15 . Тогда минимальный элемент первой строки будет равен 2 и оценка h2 h h2 ' 14 2 16

Поскольку h2			h1 , то из дальнейшего рассмотрения исключаем множество
гамильтоновых циклов (1){5} .
Будем рассматривать множество (1,5) A с матрицей весов
x			5	0	2	8
2		0		0	2
W ' 3		2	2		0	0
4	0		7	0		0
6		6	0	8	2

Минимальным элементом в первой строке этой матрицы является wx3 0 .

Поэтому разобьем множество гамильтоновых циклов из множества (1,5) A

34

на два подмножества						(1,5,3) A			и		(1,5){3}. Подмножество				(1,5,3) A содер-
1, 5, 2, 3, 4, 6 ,					1, 5, 2, 3,1				6, 4 ,					1, 5, 2, 4, 3, 6 ,	1
жит1,элементы5, 2, 4, 6, 3 ,						1, 5, 2, 6, 3, 4 ,								1, 5, 2, 6, 4, 3 ,
1, 5, 3, 2, 4, 6 ,						1, 5, 3, 2, 6, 4 ,								1, 5, 3, 4, 2, 6 ,
1, 5, 3, 4, 6, 2 ,						1, 5, 3, 6, 4, 2 ,								1, 5, 3, 6, 2, 4 ,
1, 5, 4, 2, 3, 6 ,						1, 5, 4, 2, 6, 3 ,								1, 5, 4, 3, 2, 6 ,
Для подмножества					(1,5,3) A1 построим граф G'' , который образован отож-
1, 5, 4, 3, 6, 2 ,						1, 5, 4, 6, 3, 2 ,								1, 5, 4, 6, 2, 3 ,
дествлением вершин						x	и 3 графа					G'	. Матрица весов этого графа, столбец
1, 5, 6, 3, 2, 4 ,						1, 5, 6, 3, 4, 2 ,								1, 5, 6, 4, 2, 3 ,
минимальных элементов строк и строка минимальных элементов столбцов
1, 5, 6, 4, 3, 2 ,						1, 5, 6, 2, 3, 4 ,								1, 5, 6, 2, 4, 3
имеют вид
x' 2 0						0					0
2		0		2							0
W '' 4		0	7			0		a''			0		b'' (0,0,0,0)
6		6	0	2							0
Матрица W '' получена из матрицы W ' удалением первоначальной строки
x и столбца 3 и перемещением строки 3 на первое место.
Отсюда W ''* W '' и оценка h										15 .
								11

Для подмножества (1,5){3} в матрице W '* элемент w'* 0 нужно заменить

на	w'* . В результате получим оценку h	h 2 17 .
	12	1
	Поскольку h11 h12 , то следует выбрать множество гамильтоновых цик-
лов	(1,5,3) A с матрицей весов W ''* W '' . Разобьем это множество на два
	2

подмножества (1,5,3,4) A3 и (1,5,3){4} , поскольку элемент w''* x'4 0 . Мно-

жество (1,5,3,4) A3 ={(1,5,3,4,2,6), (1,5,3,4,6,2)}.

Оценим вес гамильтоновых циклов в множестве (1,5,3,4) A3 . Для этого по-

лучим граф G''' из графа G'' отождествлением вершин x' и 4. Тогда матрица весов графа G''' имеет вид

x''			7	0
W ''' 2		0
6		6	0

Минимальные элементы всех строк и столбцов равны 0. Поэтому

h111 h11 15 и W '''* W ''' .

35

(G) m n с .

* (G) n c

Для подмножества (1,5,3){4} нужно заменить элемент w''* x'4 0 на w''* x'4 . Отсюда h112 h11 2 17 .

Поскольку h111 h112 , то рассмотрим множество

(1,5,3,4) A3 ={(1,5,3,4,2,6), (1,5,3,4,6,2)} и найдем веса циклов, входящих в

него. Учитывая, что w'''26 , вес гамильтонова цикла (1,5,3,4,2,6) равен. Второй гамильтонов цикл (1,5,3,4,6,2) имеет вес, равный 15, что соот-

ветствует оценке h111 15 . Этот цикл является гамильтоновым циклом минимального веса.

2.8. Упорядоченные и бинарные деревья

Деревом называется связный граф, не содержащий циклов. Лесом или ациклическим графом называется любой граф без циклов.

Остовом или каркасом графа G называется остовный подграф H произвольного графа G , который на каждой области связности графа G порождает дерево. В каждом графе существует остов. Из графа можно получить остов, если в каждой компоненте графа разрушить циклы, удаляя лишние ребра. Остов в графе можно найти с помощью поиска в ширину. Пусть m – число ребер графа, n – число его вершин, с –число компонент графа. Цикломатическим рангом (или цикломатическим числом) графа называется (G) m n с .Коциклическим рангом графа G называется

– число ребер любого остова графа.

Число ребер произвольного графа G , которые необходимо удалить, чтобы получить остов графа, не зависит от последовательности их удаления и равно цикломатическому числу

Граф G является лесом тогда и только тогда, когда (G) 0 . Граф G

имеет единственный цикл тогда и только тогда, когда (G) 1.. Граф G , в котором число ребер не меньше, чем число вершин, содержит цикл.

Всякий ациклический подграф произвольного графа G содержится в некотором остове графа G .

В каждом графе имеется остов. В общем случае он определен неоднозначно. В связном графе остовом является любое остовное дерево, т.е. остовный подграф, являющийся деревом. Число остовных деревьев в связном

36

графе G порядка n 2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа B(G) .

2.9. Остов минимального веса. Алгоритм Краскала.

Пусть граф G является связным взвешенным графом порядка n . Требуется найти остов минимального веса.

Решение этой задачи можно найти с помощью алгоритма Краскала.

1)	Строим граф T1 On e1 , присоединяя к пустому графу On , построен-
ном на множестве n вершин графа G , ребро e1 E минимального веса.
2)	Если граф Ti уже построен и i n 1, то строим граф Ti 1 Ti ei 1 ,
где ei 1 – ребро графа G , имеющее минимальный вес среди ребер, не
входящих в Ti и не составляющих циклов с ребрами из Ti . Такой граф при

i n 1 можно построить. Граф Tn 1 является остовом минимального веса в заданном графе G .

Граф Ti имеет i ребер и поэтому при i n 1 является несвязным. По-

скольку граф G связен, то в нем есть по крайней мере одно ребро, не составляющее циклов с ребрами графа Ti . Поэтому нужное ребро ei 1 суще-

ствует и граф Ti 1 можно построить. Граф Tn 1 является (n, n 1) графом без циклов, следовательно, он является деревом.

Методом от противного можно показать, что дерево Tn 1 имеет мини-

мальный вес.

В некоторых ситуациях требуется построить остов не минимального, а максимального веса. В этом случае также применим алгоритм Краскала, нужно лишь всюду минимальный вес заменить максимальным.

Задача 2.16 . Пусть имеются населенные пункты 1,2,3,4,5,6 (вершины графа на рис а.) и известны трассы и стоимость строительства дорог, соединяющих отдельные населенные пункты (веса ребер). Требуется определить, какие из дорог нужно построить, чтобы стоимость строительства была минимальной и можно было попасть из любого населенного пункта в любой другой пункт.

37

~

ei .

1		(6)	4	1			4
(1)		(3)	(1)			(3)	(1)
	3				3
(1)			(3)	(1)
(3)		(4)		5	(3)		5
			(2)				(2)
2		(6)	6	2			6
		а				б

Рис.2.19

Для связного взвешенного графа, изображенного на рис. , нужно найти покрывающее его дерево минимального веса. Решим эту задачу с помощью

алгоритма Краскала. На первом шаге выберем ребро e1 {1,2}. Далее из двух ребер {2,3} и {2,6} выбираем ребро с меньшим весом

e2 {2,3}. На следующем шаге ребро {3,1} выбирать нельзя так как в этом случае образуется цикл , поэтому выберем e3 {3,4} , имеющее меньший вес, чем ребро {3,6}. Далее выбираем ребра e4 {4,5} и e5 {5,6} . В ре-

зультате построено дерево T5 ( Рис 2.19 б), которое представляет собой

остов минимального веса для заданного графа.

2.10. Фундаментальные циклы и фундаментальные разрезы

Пусть G (V , E) – (n, m) неорграф, имеющий с компонент связности.

T остов графа G . Остов графа имеет (G) n c ребер, которые называются ветвями остова T . Оставшиеся m n c ребер графа, не входящие в T , называются хордами остова T .

Если к лесу добавить произвольную хорду ~ , то в полученном графе

T ei

найдется ровно один цикл Ci , который называется фундаментальным цик-

лом графа относительно хорды ~ остова . Цикл состоит из хорды

G ei T Ci

~ и некоторых ветвей остова , которые принадлежат единственной про-

ei T

стой цепи, соединяющей вершины хорды

38

Фундаментальным множеством циклов графа G относительно остова T называется множество {C1 ,C2 ,...,Cm n c } всех фундаментальных циклов относительно хорд. Число всех фундаментальных циклов графа G относительно хорд остова T равно цикломатическому числу (G) m n c .

Обозначим через ~ ~ ~ – последовательность

(e1 , e2 ,..., em n c, em n c 1 ,..., em )

всех ребер графа G , в которой первые m n c ребер являются хордами (для них введено специальное обозначение). Тогда фундаментальному цик-

				(ai1 , ai 2 ,..., aim ) , координаты которого рав-
лу Ci соответствует вектор ai
ны
aij	1,	если e j	Сi
		если e j	Сi
	0,

Тогда фундаментальное множество циклов можно задать с помощью матрицы C фундаментальных циклов, элементами строк которой являются коор-

					(ai1 , ai 2 ,..., aim ) , где i 1,2,..., (G) . Каждый фунда-
динаты векторов ai
ментальный цикл Ci						содержит ровно одну хорду ei , поэтому матрица С
имеет вид
1		0	...	0		a	...	a
						1, 1		1m
	0	1	...	0		a2, 1	...	a2 m
C ... ... ... ...						...	...	...
	0	0	...	1		a	...	a
						, 1		m

Здесь m n c . Матрица фундаментальных циклов имеет структуру C (C1 | C2 ) , где C1 – единичная матрица порядка .

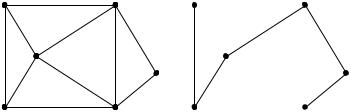
Задача 2.17 . Найти матрицу фундаментальных циклов графа G , изображенного на рис. 2.20

39

множества V1

V V1 V2

V V1 V2

5		8
4	6	2
		3
1		7

Рис.2.20

Решение. Цикломатическое число графа равно

m n c 8 6 1 3. Для получения остова графа удалим из него три ребра под номерами 1, 2, 3. Ребрам, входящим в остов, сопоставим номера 4,5,6,7,8. Фундаментальный цикл C1 , соответствующий хорде 1, состо-

ит из ребер 1,4,6; фундаментальный цикл C2 , соответствующий хорде 2,

состоит из ребер 2,6,7; фундаментальный цикл C3 , соответствующий хорде 3, состоит из ребер 3,6,7,8. . Матрица фундаментальных циклов имеет вид

			1	2	3	4	5	6	7	8
	C	1		0	0		0	1	0	0
						1
C	1										.
	С2		0	1	0	0	0	1	1	0
			0	0	1	0	0	1	1	1
	С3

Пусть G (V , E) – неорграф, – разбиение множества V

на два непересекающихся множества. Разрезом графа G по разбиению называется множество всех ребер, соединяющих вершины из с вершинами из множества V2 .

Простым разрезом или коциклом называется непустой разрез K неорграфа , если любое собственное подмножество K не является разрезом ни по какому разбиению множества V , т.е. в результате удаления из K какого либо ребра нельзя получить снова непустой разрез. Коцикл состоит из минимального множества ребер, отделяющего некоторые вершины связного графа от остальных

40