Лекция 04. Множество комплексных чисел

Лекция 4. Множество комплексных чисел.

4.1. Определение и геометрическое представление комплексных чисел.

Существуют такие алгебраические уравнения, которые не имеют действительных корней. Например, квадратные уравнения с отрицательным дискриминантом. Простейшее из них – уравнение . Введём новое число i, которое будем считать корнем уравнения . Таким образом, для числа i выполнено равенство . Символ i называется мнимой единицей.

Определение 4.1. Комплексными числами называются числа вида , где , i – мнимая единица. Числа x, y называются соответственно действительной и мнимой частями комплексного числа z и обозначаются , .

, то есть z совпадает со своей действительной частью x.

– чисто мнимое число.

Между множеством комплексных чисел и множеством точек плоскости xOy существует взаимнооднозначное соответствие.

Векторы считаются свободными векторами (то есть начало можно совместить с любой точкой плоскости, перенеся параллельно самому себе).

Вместо термина «комплексное число » можно употреблять «точка » или «вектор ».

Плоскость xOy называется плоскостью комплексных чисел или плоскостью Z. Действительные числа изображаются точками оси Ox или векторами, параллельными этой оси. Ось Ox – действительная ось.

Чисто мнимые числа изображаются точками оси Oy или векторами, параллельными Oy. Ось Oy – мнимая ось. Число – точка является единичным вектором этой оси.

Модуль комплексного числа: – длина вектора .

Два комплексных числа , равны, если

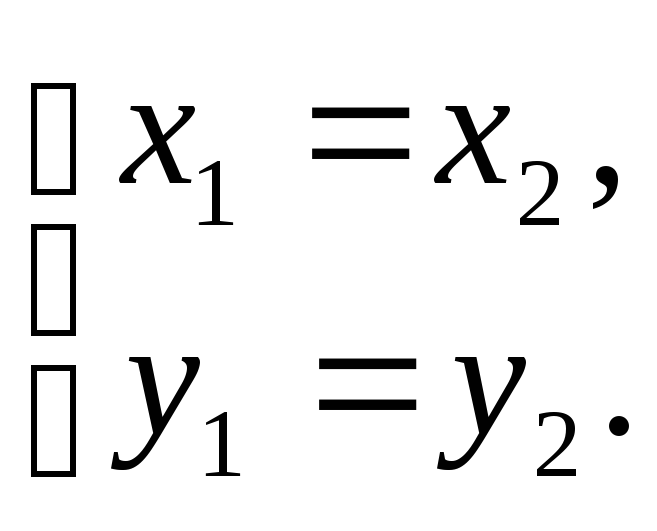
4.2. Свойства комплексных чисел в алгебраической форме.

Сумма комплексных чисел в алгебраической форме:

. (4.1)

Рассмотрим сумму комплексных чисел в векторной интерпретации.

Рис. 4.1.

На Рис. 4.1 видно, что проекции вектора равны суммам соответствующих проекций слагаемых векторов z₁ и z₂.

Законы сложения.

а) Коммутативный: ,

b) Ассоциативный: ,

c) для .

Сложение допускает обратную операцию – разность комплексных чисел:

.

На Рис. 4.1 легко увидеть, что проекции вектора равны разности соответствующих проекций z₂ и z₁. А также очевидно выполнение неравенств

, .

 Пример 4.1.

1. .

2. .

3. , , . 

Умножение комплексных чисел в алгебраической форме:

(4.2)

Законы умножения:

a) Коммутативный: , ,

b) Ассоциативный: , ,

c) Дистрибутивный: , ,

d) для ,

e) Для, где .

Число z в (e) называется частным комплексных чисел z₁ и z₂, обозначается . Деление на 0 невозможно.

Все свойства следуют из определений операций сложения и умножения и равенства комплексных чисел. Докажем (e).

♦ Пусть , , , .

.

то есть . ■

☼ Замечание 4.1. Как уже было отмечено (см. Рис. 4.1), в векторной интерпретации сложение и вычитание комплексных чисел производится по правилам сложения и вычитания векторов. Однако умножение и деление комплексных чисел, совершаемые необходимо по формулам (4.1) и (4.2), не имеют непосредственных аналогов в векторной алгебре.

Векторная интерпретация комплексного числа непосредственно применяется, например, в электротехнике для изображения переменных синусоидальных токов и напряжений. ☼

4.3. Сопряжённые комплексные числа.

Определение 4.2. Пусть . Число называется комплексно сопряжённым числом с числом и обозначается , .

Заметим, что

;

;

, .

Следовательно, полученное соотношение сводит деление комплексного числа z₁ на z₂ к умножению числителя и знаменателя на .

 Пример 4.2. . 

♦ Теорема 4.1. .

Доказательство..

■

♦ Теорема 4.2. .

Доказательство.

,

. ■

♦ Теорема 4.3. , .

Доказательство. . ■

Следствие.

1. .

2. .

♦ Теорема 4.4. Сумма и произведение сопряжённых комплексных чисел являются действительными числами.

Доказательство. – действительное число, – действительное число. ■

4.4. Тригонометрическая форма комплексного числа.

Абсциссу x и ординату y комплексного числа можно выразить через его модуль r и аргумент :

, , , .

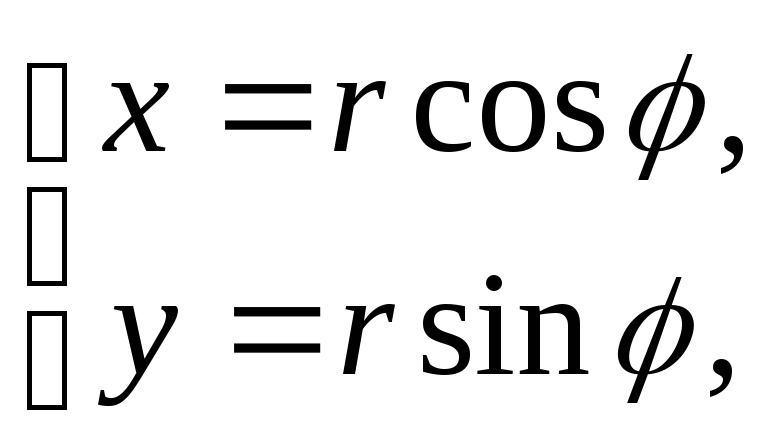– тригонометрическая форма комплексного числа.

Модуль определяется однозначно; аргумент определяется многозначно (аргументы отличаются на , ). Для определённости будем рассматривать .

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы:

Для сопряжённых чисел: , .

 Пример 4.2. Представить комплексное число в тригонометрической форме, взяв главное значение аргумента.

1) .

2) .

3) .

4) . 

Умножение комплексных чисел в тригонометрической форме.

Пусть , . Найдём произведение :

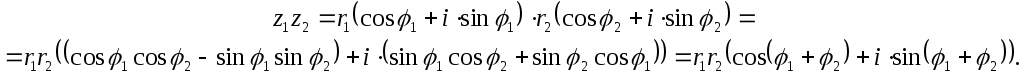
То есть , – модуль произведения равен произведению модулей, , – аргумент произведения равен сумме аргументов.

Деление комплексных чисел в тригонометрической форме.

Рассмотрим :

, .

Таким образом. получаем:

,

то есть , .

Возведение в степень.

Если – тригонометрическая форма числа z, то

.

Умножив это равенство на z, будем иметь . Для любой натуральной степени n числа z по индукции получаем формулу Муавра:

.

Таким образом, и .

 Пример 4.3. 1) ,

2) ,

3)



☼ Упражнение. Найти значения выражений:

1) , 2) , 3) . ☼

Извлечение корня.

Число называется корнем степени n (, ) из комплексного числа z, если . Таким образом, для нахождения всех корней степени n из числа z нужно найти все решения уравнения .

Если , то – единственное решение. Если , то, записав числа и z в тригонометрической форме:

,

и применив формулу Муавра, получим уравнение в виде

.

Два комплексных числа равны, если равны их модули, а аргументы отличаются на . Следовательно, , .

.

 Пример 4.4.

,

,

. 

☼ Упражнение. Найти значения выражений:

1) , 2) , 3) .

4) Решите уравнение . ☼

Отметим ещё одно интересное равенство, связывающее показательную и тригонометрическую функции. Формула Эйлера:

.

При получается, по словам Ф. Клейна, «самая удивительная формула во всей математике»: . Рассмотрим ещё одну формулу: .

☼ Упражнение. Найти , , . ☼

 Пример 4.5. Найдём , . Таким образом, получилось, что – период функции . Показательная функция с комплексным аргументом – периодическая.

Выразим тригонометрические функции через показательные: 

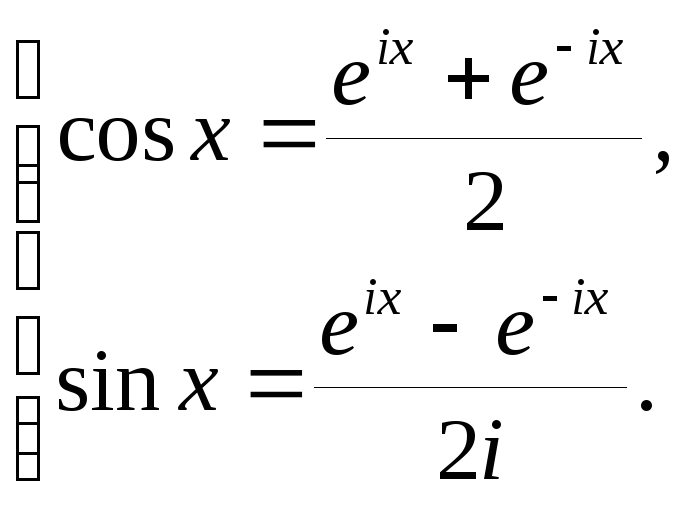
Формула Эйлера преобразует тригонометрическую форму комплексного числа в показательную форму . Показательная форма также очень удобна для выполнения операций умножения и деления комплексных чисел: и .

☼ Историческая справка. Впервые мнимые величины появились в труде Дж. Кардано (G. Cardano, 1545) «Великое искусство, или об алгебраических правилах». Пользу мнимых величин при решении кубического уравнения в неприводимом случае (когда действительные корни выражаются через кубические корни из мнимых величин) оценил Р. Бомбелли (R. Bombelli, 1572).

Он же дал простейшие правила действий с комплексными числами. В 16-17 веках выражения вида , , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми». Для многих (в т.ч. и крупных) учёных 17 века алгебраическая и геометрическая сущность мнимых величин представлялась неясной и даже загадочной и мистической. Например, И. Ньютон (I. Newton) не включал мнимые величины в понятие числа, а Г. Лейбницу (G. Leibniz) принадлежит фраза: «Мнимые числа – это прекрасное и чудесное убежище божественного духа». Символ предложил Л. Эйлер (L. Euler, 1777). Арифметическая теория комплексных чисел как пар действительных чисел была построена У. Гамильтоном (W. Hamilton, 1837). Ему же принадлежит важное пространственное обобщение комплексных чисел – кватернионы, алгебра которых некоммутативна. В конце 19 века было доказано, что всякое расширение понятия числа за пределы поля комплексных чисел возможно только при отказе от каких-либо обычных действий (прежде всего, коммутативности). ☼

21