3.4. Нахождение коэффициентов

I способ.

Пусть ,,.

Написанное равенство есть тождество, а поэтому:

а) приведя дроби к общему знаменателю, получим тождественные многочлены в числителях справа и слева;

б) приравняем числители;

в) а затем их коэффициенты при одинаковых степенях;

г) получим систему уравнений для определения коэффициентов.

Пример 25. Рассмотрим пример 21.

а) Приведем дробь к общему знаменателю:

.

б) Приравняем числители:

.

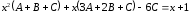в) Приравняем коэффициенты при одинаковых степенях:

(коэффициент при )

(нет коэффициента при )

(свободный член).

г) Решив систему, получим:

; ;.

Получили разложение

.

II способ.

Приравняем многочлены в числителях слева и справа, как в I способе:

д) Придадим частные значения, вычислим значения многочленов. Получим также систему с неизвестными коэффициентами.

В качестве значений удобно брать значения действительных корней знаменателя, лучше применять в случае, когда знаменатель имеет равные действительные корни.

Пример 26. ,

а)

б)

д)

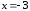
В итоге .

III способ.

Комбинируют I и II способы.

3.5. Правило интегрирования рациональных дробей

Чтобы проинтегрировать рациональную дробь, необходимо:

1. Проверить, является ли эта дробь правильной. Если дробь неправильная, выделить целую часть, разделив числитель на знаменатель.

2. Правильную рациональную дробь разложить на сумму простейших дробей.

3. Найти неизвестные коэффициенты.

4. Проинтегрировать простейшие дроби.

Пример 27.

Дробь неправильная,

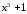
Дробь – правильная, разложим знаменатель дроби на множители:

,

.

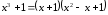IV. Интегрирование некоторых иррациональностей

Основным методом решения интегралов от иррациональных выражений является метод замены переменной.

Цель замены – преобразовать данное иррациональное выражение к рациональной дроби.

1. сводится к ,

предварительно необходимо выделить полный квадрат под знаком корня, сделать замену и проинтегрировать по таблице интегралов, 10 и 12.

Пример 28.

.

2.

1. Сделать в числителе производную подкоренного выражения.

2. Разбить на два интеграла, один из которых степенной, а другой вида (1).

Пример 29.

.

3. подстановка

–наименьший общий знаменатель дробей и.

Пример 30.

Здесь роль играет,;;, наименьший общий знаменатель этих дробей, следовательно, подстановка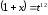, вычислим

.

4. ,;

, ;

, .

5. – дифференциальный бином интегрируется в трех случаях:

1) – целое,– интегрируется непосредственно,

– подстановка, где– общий знаменатель дробей

и;

2) – целое (,,) подстановка, где– знаменатель

дроби ;

3) – целое (,,) подстановка.

Пример 31.

.

V. Интегрирование тригонометрических выражений

1. решается универсальной подстановкой,,;.

Пример 32.

.

В некоторых случаях полезнее использовать подстановки, которые дают лучший результат, чем при использовании универсальной подстановки.

2. Если в подынтегральном выражении при замене наинафункция не меняет своего знака, т. е. если

,

то применяют подстановку .

Пример 33.

.

3. Если , т. е. при замененаподынтегральная функция меняет знак, то подстановка.

Пример 34.

.

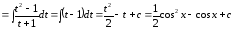4. Если , т. е. при замененаподынтегральная функция меняет знак, то подстановка.

Пример 35. .

5. ; при– четном,;

; при – нечетном по правилу 3 или 4.

Пример 36.

.

Пример 37. .

Пример 38.

.

6. ,

,

.

Пример 39. .