ФИНАНСОВАЯ МАТЕМАТИКА / Севастьянов П.В. Финансовая математика и модели инвестиций

представляющий собой нечеткий интервал, вообще говоря произвольной формы. Последний может быть получен на основе опроса экспертов, с помощью описанной выше методики трансформации произвольных частотных распределений в нечеткие интервалы или с помощью сочетания этих подходов; f (X) – совокупный доход портфеля, представляющий собой нечеткий интервал.

Представим Ri в виде разложений на a-уровни

	i = ![Rα− ,Rα+ ]i ,	(4.21)
R
	α

где Rα− , Rα+ – левая и правая границы соответствующих a-уров- ней четких интервалов.

Для совокупного дохода портфеля получаем, соответ-

ственно			(X) = ![fα− (X), fα+ (X)] ,	(4.22)
где fα− (X), fα+ (X)		f
	— леваяα и правая границы интервала,

соответствующего a-уровню целевой нечетко-интервальной

функции f (X) .

Подставляя (4.21), (4.22) в (4.20) получает две достаточно простые задачи линейного программирования, решения которых могут быть получены с помощью любого из многочисленных пакетов прикладных программ.

fα−	(X) =	∑n	Rα−	i xi	→	max,	∑n	xi	=	1,	(4.23)
fα+	(X) =	∑i=n1	Rα+	i xi	→	max,	∑i=n1	xi	=	1,	(4.24)
		i= 1					i= 1

гдеα =1,…,m; m – число используемых α -уровней. Решения можно формально представить в виде:

{xi }op− = arg max fα− ({xi }),	∑n	xi = 1, {xi }op+	= arg max fα+ ({xi }),	∑n	xi = 1.
X	i= 1		X	i= 1

Подставляя их в (4.23), (4.24) получаем интервалы, в которых может находиться оптимальный доход для каждого

161

a-уровня[f −

, f +

]

α

и соответствующие интервалы решений

op

op

[xiop− , xiop+ ]α

i =

1,...,n.

В итоге приходим к некоторому интервальному решению.

Ясно, что это не удовлетворяет практических потребностей,

поскольку инвесторы всегда желают знать четкие, а не интер-

вальные значения xi .

Поэтому продолжим наши рассуждения.

Построим нечеткий интервал на основе четких

интервалов[f −

,

f +

]

α

(рис. 4.8).

op

op

α

λf

m− 1

0.5

µ f

fopo−

fop− α

fop− 1

fop+ 1

fop+ α

fopo+

fop

Рис. 4.8. Построение нечеткого интервала допустимых значений дохода и функции желательности дохода

Соответствующую функцию принадлежности представим в виде:

	0,			f		op	< f −	,	f	op	> f +
							opo				opo
µ f ( fop ) =				fop− 1 < fop < fop+ 1
	1,
			α
						,	fopo−	≤	fop	≤	fop− 1, fop+ 1 ≤ fop ≤ fopo+ .
	m −			1
Способ формализации									f	отражен непосредственно на
рис.4.8.

162

Очевидно, что граничные значения fopo− , fopo+ определяют область достижимых оптимальных решений, а значения

µ	f	– степени возможности их реализации при исходной нео-
пределенности R . Зная fopo−			, fopo+	можно построить реалис-
		i

тическую функцию желательности дохода λ f на этом базисе

(рис. 4.8).

Получим двухкритериальную задачу с точки зрения же-

лательности максимизации дохода (частный критерий λ f) при

учете осуществимости этого желания ( µ f).

Обобщенный критерий можно представить разными способами:

	D1( f ) = min(µ βf1( f) ,λβ f2( f) ),
	D2 ( f ) = β 1µ f ( f) + β 2λ f( f) ,
	D3 ( f ) = µ βf1( f) λβ f2( f) ,
β ,	β – ранги частных критериев.
1	2
	Очевидно на основе одного из способов свертки част-

ных критериев в обобщенный, можно найти решение соответствующей задачи оптимизации:

f op ,k = arg maxf Dk ( f ), k = 1,2,3.

Далее определяется (приближенно), какому a-уровню соответствует найденное решение f op,k . (Речь идет об a- уровнях исходного интервала с функцией принадлежности µ f

(f).) Таким образом находим некоторый áор , приближенно

соответствующий f op,k .

Для этого áор решаем заново задачу (4.24) и получаем{xi+ }αop , а также соответствующее f ({xi+ }αop ) – прогнозируемый оптимальный четкий доход.

163

Таким образом, на основе исходной нечеткоинтервальной постановки задачи оптимизации портфеля ценных бумаг получает вполне четкое итоговое решение.

Рассмотрим более общий подход к решению задачи (4.19), (4.20).

При этом будут использоваться результаты рассмотренной выше приближенной методики, которую в связи с этим будем называть первым этапом решения задачи.

Пусть xi – четкое число и d (f (X)) – четкое значение, например, эффективной ширины нечеткого интервала f (X) (или меры его нечеткости). В принципе, можно использовать сразу несколько показателей, характеризующих степень неопределенности нечетко-интервальных данных.

Пусть m(f (X)) аналог математического ожидания (применительно к нечетко-интервальным распределениям):

m =

(X)µ

( f )df

µ( f) df , где (f) – функция принадлежности

∫

f

∫

нечеткому интервалу

(X ). На основе d и m можно построить

f

функции

ì1 (m) – критерий максимума дохода и

ì2 (d) –

критерий минимума риска .

Пусть β 1

и β 2 – ранги этих критериев. Тогда требуется

решить задачу

{xi

}op = arg max(min(µ 1β 1 (m(

{xi })),µ β22 (d (

{xi })))),

∑n

xi =

1.

f

f

{xi }

i= 1

Полученная задача нелинейного программирования решается с большими трудностями из-за ограничения ∑n xi = 1.

i= 1

Поэтому целесообразно использовать метод штрафных функций. Введем для этого штрафную функцию

D(X) =

−

k

1−

∑

n

x

, 0

≤

D(X) ≤ 1.

exp

i

164

i= 1

Тогда задача переформулируется в виде:

{xi }op =

arg max(min( 1β 1

, β22

,D)), xi ≥

0, i = 1,...,n.

{xi }

1

1

μ2(d)

μ1(m)

0			0

m

d

Рис.4.9. Функции желательности частных криериев

Чтобы сузить области поиска решений целесообразно использовать в качестве ограничений для xi интервалы оптимальных решений, полученные на первом этапе решения задачи, описанном выше.

Остается проблема конкретизации функций 1 и 2 .

За основу возьмем промежуточные результаты первого этапа решения задачи.

Тогда можно принять, что m должно находиться в области допустимых оптимальных значений, откуда следует:

1(m) = λ f(m).

Далее, можно утверждать, что максимальная ширина интервала d не может быть больше ширины интервала

[fopo− , fopo+ ], т.е. не выше ширины интервала нулевого a-уровня допустимых решений.

В этом случае для 2(d) получим функцию, представленную на рис. 4.10.

165

1

μ2(d)

0 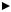f opo+ − f opo− d

Рис. 4.10. Построение функции желательности m2(d)

Представленная двухэтапная методика решения задачи оптимизации портфеля ценных бумаг в условиях нечетко-ин- тервальной неопределенности не намного сложнее в реализации, чем классические задачи на основе теоретико-вероят- ностной трактовки неопределенностей.

ЛЕКЦИЯ 5. СТАТИСТИКА И ТЕОРИЯ

ФИНАНСОВОГО РЫНКА

Цель анализа финансового рынка – разработка рекомендаций для инвесторов, в какие ценные бумаги вкладывать капитал и в каком количестве. Выше было рассмотрено решение задачи оптимального выбора портфеля ценных бумаг, однако оно носило формальныйхарактер, поскольку опиралось на предположение о том, что эффективности вложений являются случайными величинами с заданными вероятностными характеристиками. Фактически требуется знание вектора математических ожиданий и матрицы ковариаций эффективностей.

5.1. Прямой статистический подход к прогнозированию

стоимости ценных бумаг на основе исследования истории рынка. Основы метода ведущих факторов

Вразвитых странах регулярно публикуются сведения

обиржевом курсе ценных бумаг, прежде всего акций ведущих компаний. Таким образом, можно проанализировать последовательности, отражающие историю курсов и выплачиваемых дивидендов за достаточно длительный пери-

166

од. Имея эти данные, можно построить последовательности реальных эффективностей ценных бумаг за каждый квартал согласно определению:

Если R (t) – эффективность ценных бумаг j-го вида за период t , то она равнаj

( t )	=	C(j t+ 1 ) + d (j t ) − C(j t ) ,		(5.1)
R j
		C(j t )

где С (t) – цена в начале периода t, d (t) – дивиденды за период t.

Кварталj выбранвкачествеединицыj времени, посколькуданные о выплате дивидендов принято публиковать ежеквартально.

В действительности теоретическая формула (5.1) должна быть уточнена. Следует учесть, что цена покупки (bid price) и цена продажи (ask price) различны, даже если эти операции относятся к одному и тому же периоду времени. Именно эта разность (bid-ask spread) составляет основной источник заработка профессионального торговца акциями (дилера). Эффективность вклада должна оцениваться по общему итогу опера- ции, состоящей из покупки у дилера ценных бумаг по цене Cj(t) (ask price начала периода), получения дивиденда за период и продажи в конце периода (начале следующего) по цене Cj(t) (bid price), которая ниже ask price того же моментаC j (t) на установленный для данного типа ценных бумаг процент (в среднем ~ 1%, но для акций крупных компаний процент ниже, а для мелкихвыше, чтоотражаеттрудоемкостьсбытаменеесолидныхценных бумаг). Таким образом, уточненная формула имеет вид:

		C (jt + 1)	+		d (jt) −			j(t) .
(t)	=						C			(5.2)
R j
				C j(t)

Предположим, что ряды таких данных подготовлены соответствующей информационной службой. Теперь необходимо связать их с принятой ранее теоретической моделью, в которой эффективности трактовались как случайные величины.

Логически простейший путь заключается в следующем: предположим, что наблюдаемые последовательности {R (t), t=1, ..., T; j = 1, ..., n} являются реализациями, выборками jиз совокупности случайных величин {Rj}, и, более того, значения эффективностей в будущем (t > Т) также являются реализацией той же совокупности. 167

Эта гипотеза открывает принципиальную возможность статистической оценки параметров, характеризующих величины Rj. Эти оценки принято именовать «историческими» (historical) или «архивными», поскольку они строятся на основе истории ценных бумаг, данные о которых хранятся в компьютерных архивах финансовых аналитиков.

В соответствии с правилами статистики можно ввести оценки математических ожиданий как средних по выборкам:

			$T
			mj
V$jT =	1		∑T
	T −
		1 t= 1

=	1		∑T	R(jt) ,
		T
			t = 1					).
	(t)		−	$T	(t)	−	$T
(Ri				mj	)(Rj		mj

(5.3)

(5.4)

Реальные цифры таковы. Число ведущих компаний, акции которых котируются на биржах США и составляют основную (по общей стоимости) часть рынка, обычно оценивается в n = 500 (такое число учитывается в наиболее популярном издании «Standard and Poor’s Index»). Длительность ежеквар-

тальных временных рядов, имеющих смысл для статистической обработки, Т=100 (экономические условия и даже сам список ведущих компаний за период более 25 лет слишком сильно изменяются, чтобы столь устаревшие данные считать представляющими ту же генеральную совокупность). Таким образом, общий объем информации составляет 5 ? 104 чисел. Оценке же подлежат n величин mj и n(n+1)/2 различных величин Vij. При n = 500 получаем, что требуется оценить более 105 величин Vij, т. е. больше, чем исходных данных. Поэтому оценки ковариаций окажутся заведомо неточными.

В силу этого обстоятельства прямой статистический подход используется только для вычисления оценок mj , а также для оценки ковариаций между «самими главными» акциями в небольшом количестве, например в количестве 30, на базе которых выводится знаменитый индекс Доу-Джонса. При этом число данных – 3000, а число оцениваемых величин – 500, что не так уж плохо.

Однако финансовый аналитик обязан давать рекомендации не только по немногим ведущим, а по возможно большему числу компаний, выдвигающих свои ценные бумаги на

168

рынок (например, наиболее подробный в CIIIA Wilshire Index учитывает 5000 видов ценных бумаг).

В экономической жизни все взаимосвязано, но есть факторы, которые влияют сразу на все показатели. Например, уровень цен на ближневосточную нефть влияет на котировку акций почти всех компаний США, поскольку эта нефть покрывает более половины энергетических потребностей США. Если цена на нефть поднимется, то станет дороже бензин для автомобилей, уменьшится спрос на бензин, на сами автомобили, на металл для их изготовления, повысятся цены на сельскохозяйственные продукты, поскольку затраты на топливо – основной компонент их себестоимости.

Рассмотрим один из таких ведущих факторов, не определяя пока его природу. Обозначим его F и будем считать, что эффективности всех вложений зависят от него. Простейшая форма зависимости – линейная, так что примем гипотезу

Rj = aj + bj F.

(5.5)

Проверим эту гипотезу и оценим значения величин aj, bj при помощи простейшей процедуры – метода наименьших квадратов.

Нанесем на диаграмму (рис. 5.1) точки с координатами Rj(t) – эффективности и F(t) – ведущего фактора за период t. Проведем прямую с минимальной суммой квадратов отклонений. Тангенс угла наклона на этой прямой даст оценку b^j коэффициентов bj , а отрезок, отсекаемый ею на оси Rj , даст оценку a^j ожидаемого значения j-го случайного коэффициента аj.

	Rj
			•	•
			•	•
	•	•	•
	•	a∩ j	•
	•			F

Рис. 5.1. Линейная аппроксимация зависимости между исходными данными

169

Формальная процедура построения такой прямой приводит к следующим простым формулам:

$

V$Fj

$

$

$

$

где

bj =

$

, a j

=

mj

− bj mF

,

VF

$

1

T

(t)

$

1

T

(t)

mj

=

∑

Rj

, mF =

∑

F

,

T

T

t = 1

t= 1

$

1

T

(t)

$

(t)

$

$

1

T

(t)

$

2

VFj

=

∑ (F

−

mF )(Rj

−

mj ); VF

=

∑ (F

−

mF )

,

T −

T −

1 t = 1

1 t= 1

(5.6)

(5.7)

$ $	– статистические оценки ожидаемых значений
т.е. mj ,mF

эффективностей Rj и фактора F,V$Fj – оценки ковариации

эффективности и фактора, aV$F – оценка вариации самого фактора.

Если гипотеза верна, то все отклонения от прямой вверх и вниз действительно являются случайными, и если в будущем возникнет новая ситуация, новая пара величин R(t)j, F(t), то соответствующая точка расположится где-то в окрестности прямой.

Средний квадрат отклонений от прямой, найденный по истории ценной бумаги, дает оценку вариации aj, которую назовем Vej. Такие расчеты можно провести по всем интересующим видам ценных бумаг.

Если ведущий фактор выбран удачно, то его влиянием определяются все случайные колебания эффективности, а собственные случайные отклонения ej от детерминированной линейной связи оказываются взаимно некоррелированными. Таким образом, приходим к уточненной гипотезе

		+ bjF + ej ,	(5.8)
Rj = aj

где e удовлетворяют условию отсутствия корреляции

j

Е{е,е} = 0, при i ≠ j,

(5.9)

170