
- •Тема 6 Гидростатика
- •6.1. Силы, действующие на жидкость. Давление. Единицы измерения давления
- •6.2. Закон Паскаля
- •6.3. Дифференциальное уравнение равновесия жидкости
- •6.4. Виды давления ( барометрическое, абсолютное, избыточное, манометрическое )
- •6.5. Приборы для измерения давления
- •6.6. Сила давления жидкости на плоскую стенку
- •6.7. Простейшие гидравлические машины
- •6.8. Закон Архимеда
- •6.9. Равновесие и остойчивость тел, полностью погруженных в жидкость
Тема 6 Гидростатика
1. Силы, действующие на жидкость. Давление. Единицы измерения
давления.
2. Закон Паскаля.
3. Дифференциальное уравнение равновесия жидкости.
4. Виды давления ( барометрическое, абсолютное, избыточное,
манометрическое ).
5. Приборы для измерения давления.
6. Сила давления жидкости на плоскую стенку.
7. Простейшие гидравлические машины.
8. Закон Архимеда.
9. Равновесие и остойчивость тел, полностью погруженных в жидкость.
6.1. Силы, действующие на жидкость. Давление. Единицы измерения давления
Рассечем жидкость, находящуюся в объеме V (например, сосуде) некоторой поверхностью на две части I и II ( рис. 15 ).
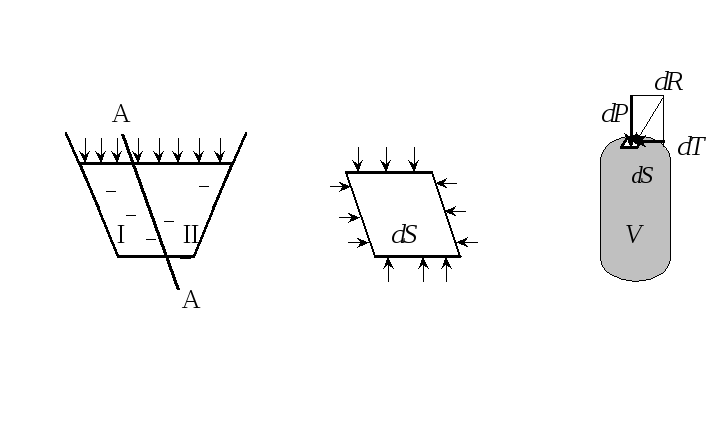
а б в
Рис. 15
Рассмотрим жидкость в объеме I. Все, что окружает этот объем, отбросим (дно, боковые стенки и т.д.) и действие отброшенного объема жидкости заменим соответствующими силами. Эти силы называются поверхностными.
Кроме них на жидкость действуют еще массовые силы (силы тяжести и инерции), которые пропорциональны массе тела.
Выделим из жидкости некоторый объем. Возьмем на поверхности этого объема бесконечно малую площадку dS. Hа эту площадку действует поверхностная сила dR. Разложим эту силу на нормальную dP и касательную dT.
Hормальная сила, приходящаяся на единицу площади, называется давлением и обозначается буквой p, т.е.
![]() .
.
В
системе СИ давление
измеряется
в
![]() .
.
|
Рис. 16 |
Сила трения (касательная сила), приходящаяся на единицу площади, обозначается буквой t, т.е.
Сила трения
обычно пропорциональна градиенту
скорости
|
Для жидкости,
находящейся в равновесии (в покое), сила
трения равна
нулю, так как в этом случае![]() .
.
6.2. Закон Паскаля
Если в жидкости взять любую точку, то на основании основного уравнения гидростатики
![]()
давление в этой
точке равно давлению, приложенному к
свободной
поверхности, плюс
![]() ,
где
,
где
![]() - глубина точки.
- глубина точки.
Таким образом мы получили закон Паскаля.
Закон Паскаля. Давление, приложенное к свободной поверхности, передается во все точки жидкости без изменения.
6.3. Дифференциальное уравнение равновесия жидкости
Запишем уравнение Эйлера
![]() .
.
Если жидкость покоится
![]() .
.
Дифференциальные уравнения равновесия жидкости в проекции на оси декартовой системы координат могут быть записаны так
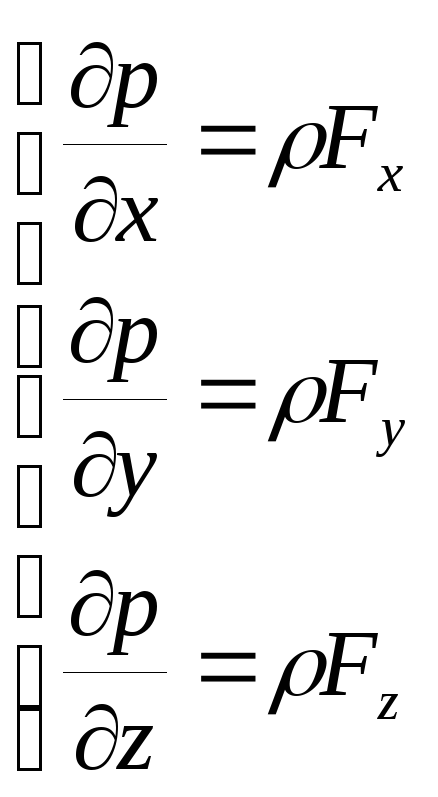 .
.
Здесь Fx, Fy, Fz - проекции на оси x,y,z сил, действующих на единицу массы рассматриваемой жидкости.
Умножая давления соответственно на dxdydz и складывая их, получаем
![]() .
.
Левая часть уравнения представляет полный дифференциал
![]() ,
,
следовательно, и правая часть должна быть также полным дифференциалом, для этого необходимо и достаточно, при постоянном r, чтобы существовала функция U(x,y,z) такая что
![]() ,
,
![]() ,
,
![]() .
.
Имеем
![]() .
.
Проинтегрировав, получим
![]() ,
,
где С - постоянная интегрирования.
Если в какой-либо точке известно давление po и постоянная функция Uo, то
![]() ,
,
из интеграла имеем
![]() .
.
В частности, когда жидкость находится в поле сил тяжести
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
![]()
Уравнение для давления принимает вид
![]() .
.
Свободная поверхность жидкости плоская z=const. При равновесии жидкости в поле земного тяготения поверхности уровня представляют собой горизонтальные плоскости.
Рассмотрим примеры.
Пример 1. Определить уравнение свободной поверхности жидкости в сосуде, движущемся горизонтально с ускорением а.
Решение. На жидкость действуют сила тяжести и сила инерции, т.е.
![]() ,
,
![]() ,
,
![]() .
.
|
|
Имеем
откуда
- уравнение прямой. |
Следовательно,
свободная поверхность представляет
собой плоскость,
наклоненную к горизонту под углом
![]() ,
который определяется из равенства
,
который определяется из равенства
![]() .
.
Пример 2. Определить уравнение свободной поверхности жидкости в сосуде, вращающемся вокруг вертикальной оси с угловой скоростью w .
Решение. Вследствие трения о стенки сосуда жидкость будет вращаться с такой же угловой скоростью. Жидкость будет находиться в относительном покое. Поэтому при решении задачи применимы уравнения равновесия.
|
|
Из массовых сил на жидкость действует центробежная сила и сила тяжести. Центробежная сила, действующая на массу m, находится на расстоянии r от оси вращения ( рис. 18 )
Проекции силы на оси, отнесенные к единице массы, будут
Тогда
|
Откуда
![]() ,
,
т.е. свободная поверхность - параболоид вращения.

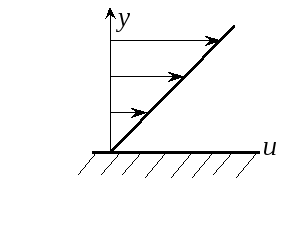
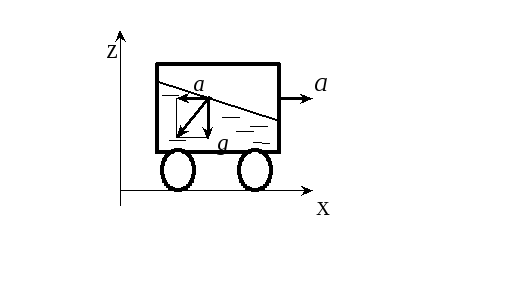 Рис.
17
Рис.
17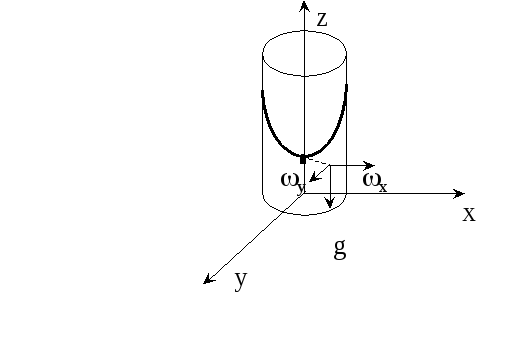 Рис.
18
Рис.
18