Представление древовидных н сетевых структур в памяти эвм

Древовидные структуры. При физической организации древо­видных структур данных в памяти ЭВМ необходимо решить два вопроса :

1) как организовать данные, представленные вершинами (узла­ми древовидной структуры) ;

2) как организовать связи между данными, представленные в схеме БД дугами древовидной структуры.

Для упрощения считаем, что данные в узле структуры можно представить последовательным списком элементов фиксированного размера, т. е. записями фиксированной длины. Поэтому рассмот­рим способы организации связи между узлами в древовидной структуре данных.

Древовидная структура - это связный неориентированный граф, который не содержит циклов. Рассмотрим еще два вспомогательных определения. Разбиением } множества называется множество подмножеств(причем, ) та­ких, что их объединение есть множество А и они являются попарно непересекающимися:

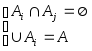для любых i не равных j

Вложенным множеством называется непустой набор } непустых множеств таких, что для любых двух множеств выполняется одно из следующих трех условий:

Таким образом, разбиение исходного множества и возможные последующие уточнения этого разбиения могут образовывать вло­женное множество.

Деревья, эквивалентные набору вложенных множеств, назы­вают ориентированными деревьями. Если линейно упорядочить элементы, то произойдет линейное упорядочение всех классов эквивалентности. В этом случае получают упорядоченное де­рево. Поскольку получена линейная упорядоченность множества В, упорядоченное дерево можно представить линейным списком.

Двоичным (бинарным.) деревом называется упорядоченное де­рево, в котором:

1) каждый произвольный узел, кроме концевого, имеет не бо­лее двух исходящих узлов (потомков или сыновей);

2) каждый сын произвольного узла идентифицируется как ле­вый или правый сын.

Поддерево Т, корнем которого является левый сын узла и, называют левым поддеревом узла v. Поддерево Т, корнем кото­рого является правый сын узла v, называют правым поддеревом узла v. Все узлы в Т располагают левее всех узлов в Т, т. е. при представлении двоичного дерева считают, что множество сы­новей каждого узла упорядочено слева направо.

Обобщением двоичных деревьев является сбалансированное (или регулярное) дерево. В сбалансированном дереве количество исходящих узлов из любого произвольного узла может быть больше двух, однако обязательно из каждого произвольного узла (кроме концевого) исходит одинаковое количество порожденных узлов. Процесс включения новых узлов в сбалансированное дерево вы­полняется сверху вниз, а на каждом уровне дерева- слева на­право. Сбалансированные деревья используются для построения индексов файлов.

Сбалансированное дерево называется полным, если для неко­торого целого числа k каждый узел глубины, меньшей, k имеет r исходящих узлов и каждый узел глубины k является концевым узлом. Глубина узла v в дереве -это длина пути из корня в v. Высотой узла v в дереве называется длина самого длинного пути из v в один из концевых узлов. Уровень узла v в дереве равен разности между высотой дерева и глубиной узла v (уровень кон­цевых узлов имеет номер 0, следующий уровень- 1 и т. д.).

Количество узлов полного сбалансированного дерева высо­ты k:

где г - количество исходящих узлов. В случае двоичного дерева r=2 и формула упрощается:

Методы представления древовидных структур линейным спис­ком с последовательным распределением памяти.

Метод ис­пользования адресной арифметики. Метод хорошо применим к сбалансированным (регулярным) деревьям. В этом случае узлы представляются записями фиксированной длины. Пусть для размещения одного узла дерева требуется квант па­мяти размером т единиц.

Первый способ. В имеющемся векторе памяти А в первом кван­те А[1] с адресом помещают корень дерева. Кванты

заполняют непосредственными потомками корня дерева. После­дующие r квантов заполняют непосредственными потомками узла, размещенного в кванте А[2]. Далее г квантов заполняют непосред­ственными потомками узла, размещенного в кванте A[3], и т. д.

Адрес k-го кванта А[k] вычисляют по формуле:

В зависимости от значения г определим функциональную за­висимость между адресами квантов, в которых размещаются узел и его непосредственные потомки.

Для случая г=2. Этот вариант рассмотрен в (списковые структуры)

Для случая r=3. Непосредственные потомки кванта A[k] это кванты A[3k-1], A[3k] и A[Зk+1] с адресами

Чтобы получить адрес узла, являющегося исходным для узла, размещенного в кванте А[k], необходимо k разделить на 3 и округ­лять до целого значения по общим правилам округления. Адрес определяют по формуле

Для случая г = 4 использование данного способа несколько осложняется. Это связано с тем, что для получения адреса узла, являющегося исходным для узла, размещенного в кванте A[k], требуется разрабатывать специальный алгоритм вычисления.

Структура, полученная при данном способе представления, поз­воляет осуществлять поиск узлов в прямом (от корня) и в обрат­ном (к корню) направлениях.

Второй способ. Применим только для двоичных сбалансирован­ных деревьев. Если используется вектор памяти от кванта i до кванта j включительно, то корень дерева помещается в квант A[l] где

т. е. в середину вектора памяти. В квантах памяти от i до (l-1) включительно размещается левое относительно корня поддерева а в квантах от (l+1) до j включительно -правое относительно корня поддерево. Размещение поддеревьев выполняется аналогич­но, корень левого поддерева размещается в квант

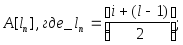
корень правого поддерева - в квант

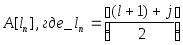
Адреса квантов вычис­ляются по формуле . Структура, полученная при данном способе представления, приспособлена для поис­ка узлов в прямом направ­лении.

Рассмотренная струк­тура еще называется де­ревом сравнений, посколь­ку используется для орга­низации данных при логарифмическом или бинарном поиске.

Метод использования левосписковых структур. Метод строит последовательность узлов при обходе исходной древовидной структуры сверху вниз и слева направо. Алгоритм по­строения последовательности в данном методе следующий. Выби­раются узлы, начиная от корня дерева и до концевого узла включительно по крайней левой ветви дерева, затем осуществляется подъем вверх до первой следующей ветви, и процесс повторяется. Узлы, ранее выбранные, в последовательность не включаются.