
- •Інтегральне числення функцій однієї змінної (конспект лекцій)
- •Таблиця інтегралів
- •Заміна змінної в невизначеному інтегралі (метод підстановки)
- •4.Інтегрування частинами у невизначеному інтегралі
- •Інтегрування раціональних функцій
- •Інтегрування деяких ірраціональних функцій
- •7. Інтегрування деяких виразів, що містять тригонометричні функції
- •8. Використання таблиць інтегралів
- •9. Поняття про інтеграли, що не виражаються через елементарні функції
- •10. Приклади задач, що приводять до поняття визначеного інтеграла
- •2)Задача про шлях точки у прямолінійному русі.
- •11. Означення визначеного інтеграла
- •12. Основні властивості визначеного інтеграла
- •13. Інтеграл як функція верхньої межі. Формула Ньютона-Лейбніца
- •14. Метод заміни змінної у визначеному інтегралі
- •15. Інтегрування частинами у визначеному інтегралі
- •16. Загальна схема застосування визначеного інтеграла
- •17. Обчислення площі плоскої фігури
- •18. Обчислення довжини дуги
- •19. Обчислення об’єму тіла
- •20. Обчислення площі бічної поверхні тіла обертання
- •21. Обчислення роботи змінної сили
- •22. Обчислення сили тиску рідини на вертикальну пластину
- •23. Невластивий інтеграл по нескінченному проміжку
- •24. Ознаки збіжності невластивого інтеграла по нескінченному проміжку
- •25. Невластивий інтеграл від необмеженої функції
- •26. Ознаки збіжності невластивого інтеграла від необмеженої функції
- •27. Наближене обчислення визначених інтегралів
26. Ознаки збіжності невластивого інтеграла від необмеженої функції
Теорема.
Якщо на проміжку
![]() функції
функції![]() і
і![]() неперервні,
неперервні,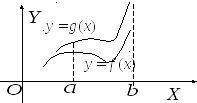 мають
особливу точку
мають
особливу точку![]() і задовольняють нерівність
і задовольняють нерівність![]() ,
то
,
то
а
Рис. 22![]()
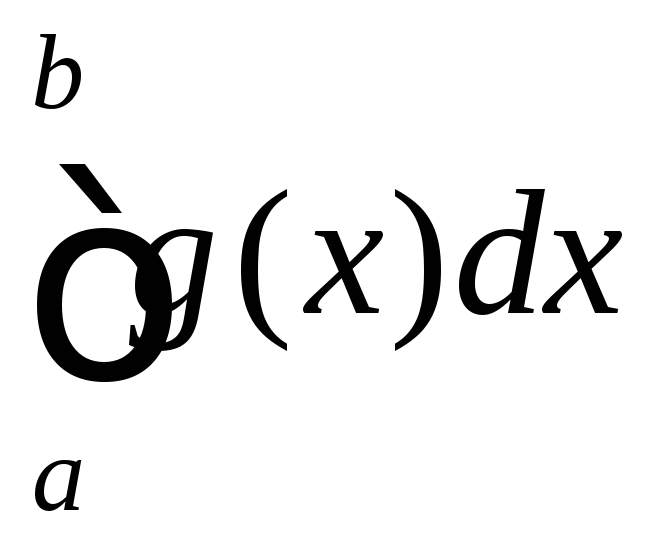 ,
то збігається і
,
то збігається і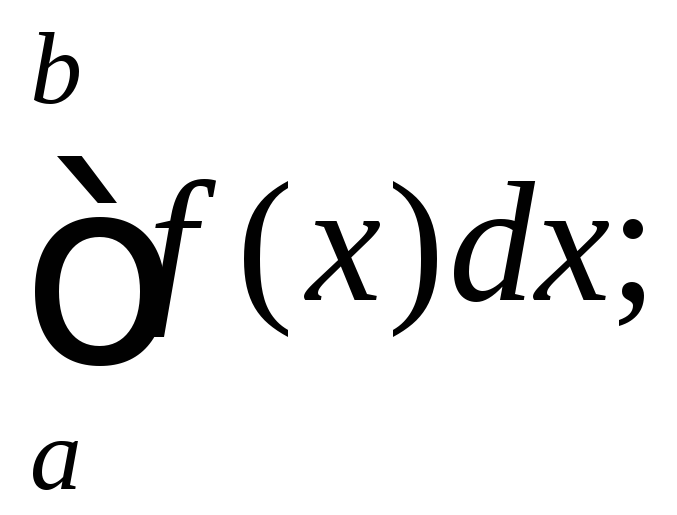
б)
якщо розбігається інтеграл
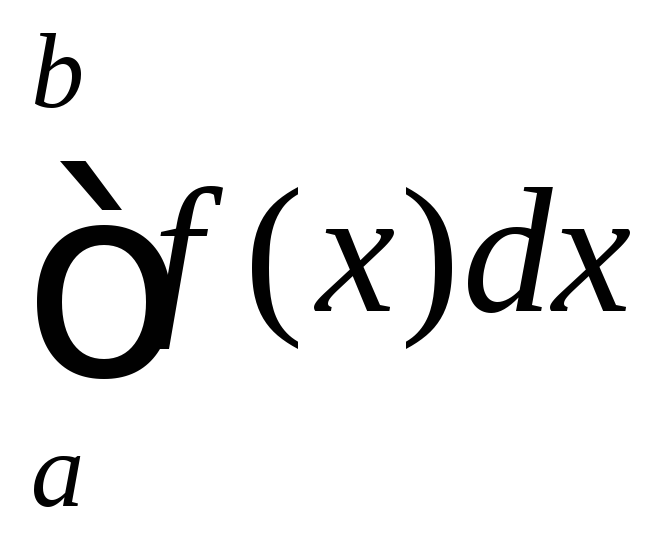 ,
то розбігається і інтеграл
,
то розбігається і інтеграл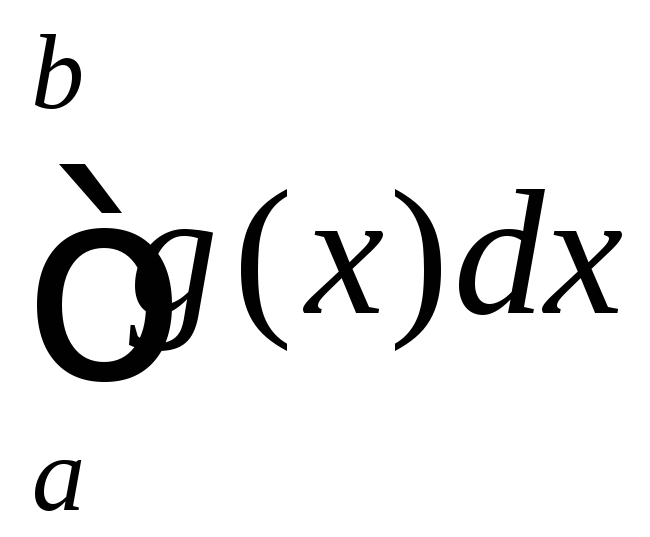 .
.
Ця
достатня умова збіжності (чи розбіжності)
невластивих інтегралів називається
ознакою
порівняння
і за своїм геометричним тлумаченням
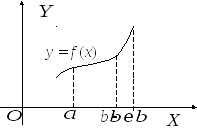 цілком
аналогічна до відповідної ознаки для
невластивих інтегралі по нескінченному
проміжку ( див. рис. 22)
цілком
аналогічна до відповідної ознаки для
невластивих інтегралі по нескінченному
проміжку ( див. рис. 22)
Рис. 22![]()
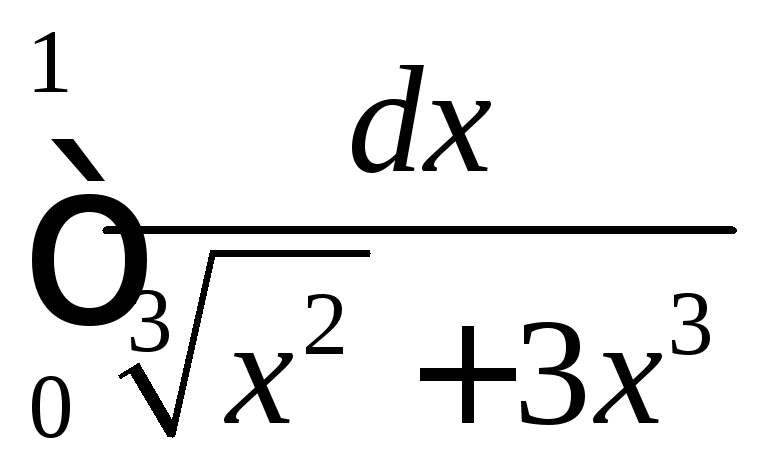 . Оскільки для всіх
. Оскільки для всіх![]() має місце нерівність
має місце нерівність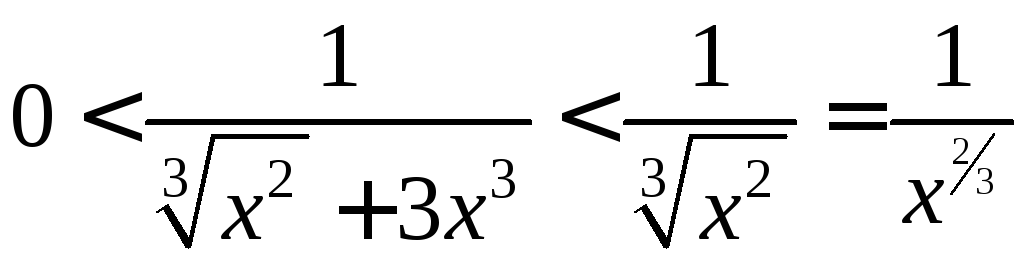 ,
а
,
а![]() і
і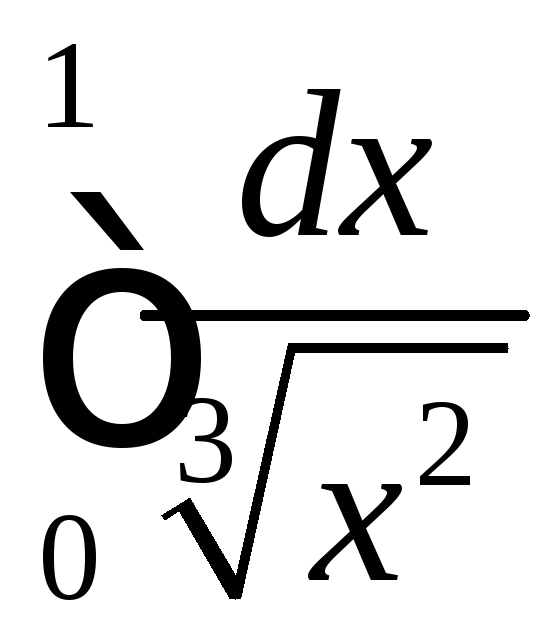 збігається (див. попередній приклад),
то і заданий інтеграл збігається.
збігається (див. попередній приклад),
то і заданий інтеграл збігається.
Теорема. (ознака порівняння в граничній формі)
Якщо
функції
![]() і
і![]() неперервні і приймають додатні значення
в проміжку
неперервні і приймають додатні значення
в проміжку![]() ,
а при
,
а при![]() мають особливу точку і існує границя
мають особливу точку і існує границя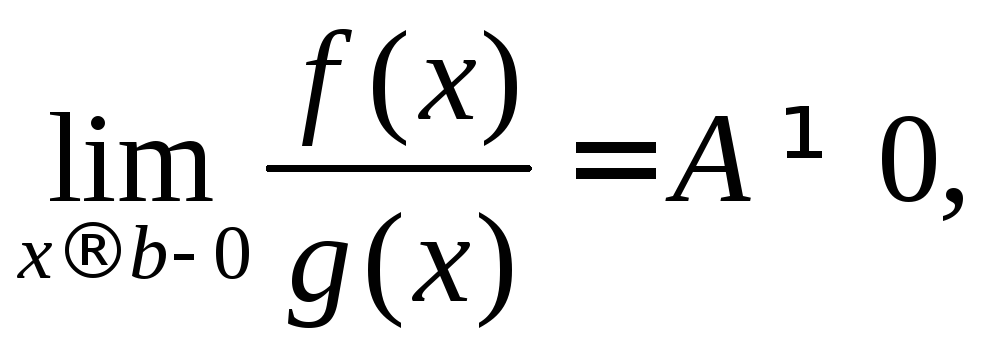 то інтеграли
то інтеграли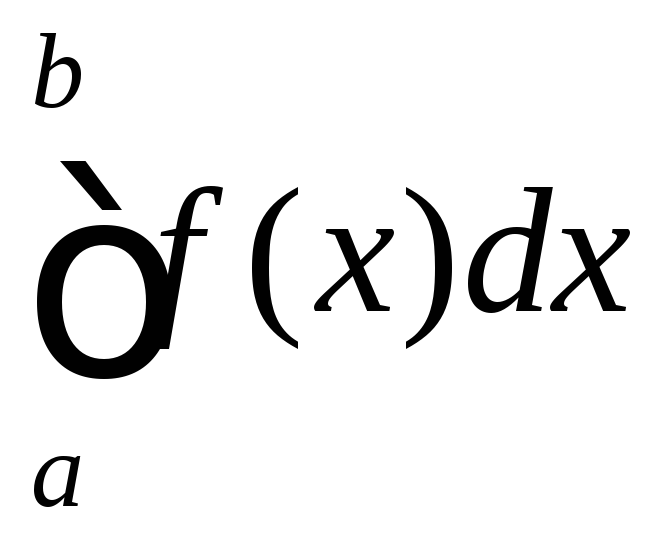 і
і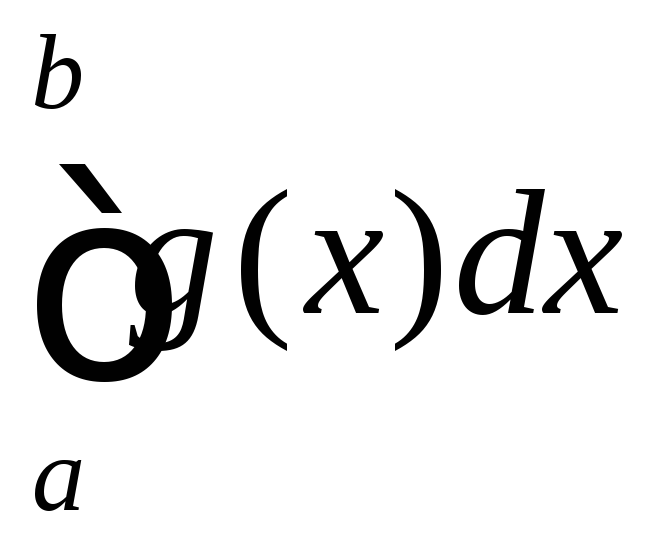 або обидва збігаються або обидва
розбігаються.
або обидва збігаються або обидва
розбігаються.
Приклад.
Дослідити на збіжність інтеграл
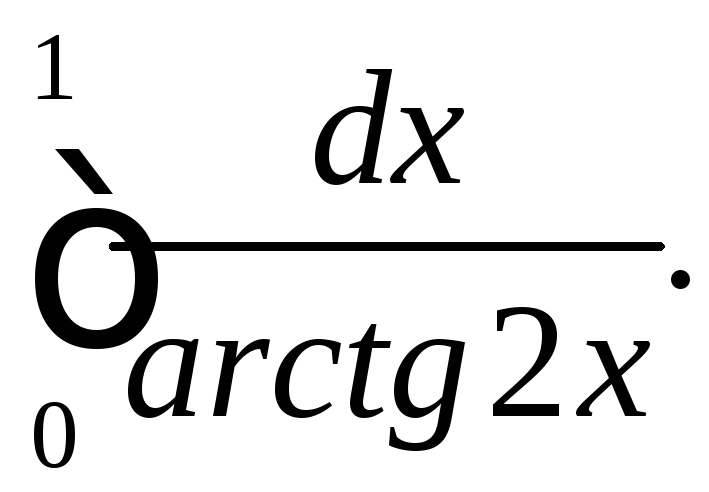
Функції
 і
і мають особливу точку
мають особливу точку![]() .
Оскільки існує границя
.
Оскільки існує границя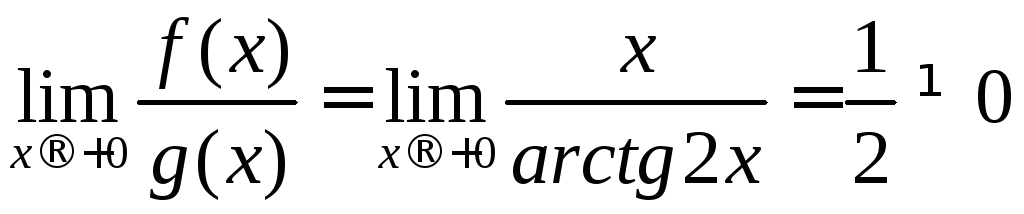 і інтеграл
і інтеграл![]() розбігається, то розбігається і заданий
інтеграл.
розбігається, то розбігається і заданий
інтеграл.
Ознаки порівняння придатні лише у випадку знакосталих підінтегральних функцій. Збіжність невластивого інтеграла від знакозмінної функції в деяких випадках можна виявити за допомогою наступної достатньої умови.
Теорема.
Якщо функція
![]() має особливу точку на відрізку
має особливу точку на відрізку![]() і інтеграл
і інтеграл
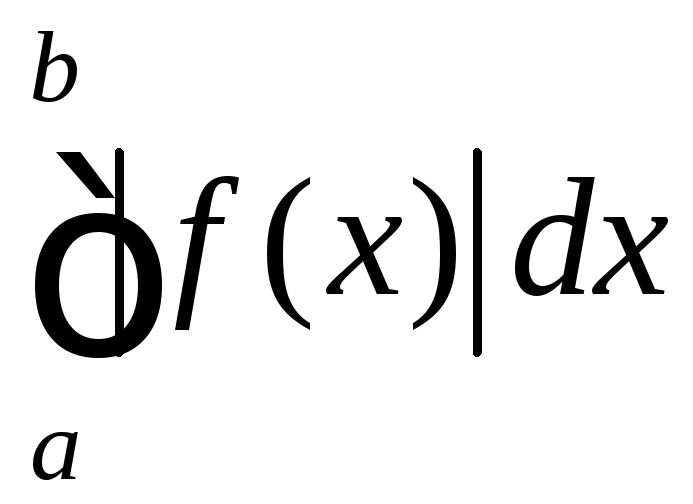 збігається, то збігається і інтеграл
збігається, то збігається і інтеграл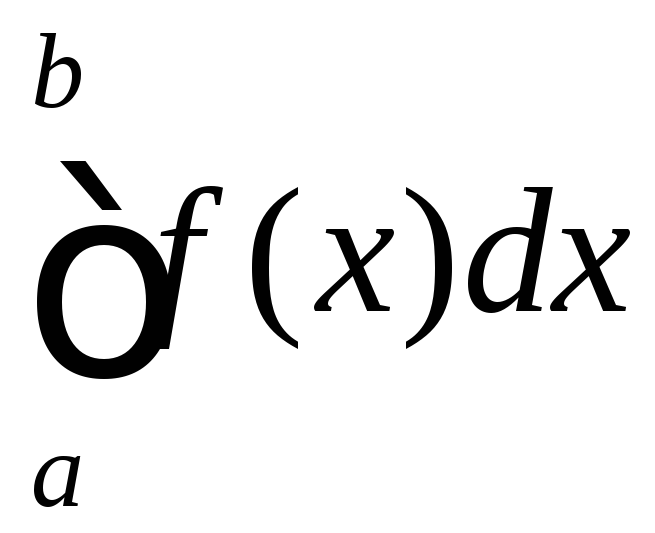 .
.
В цьому
випадку інтеграл
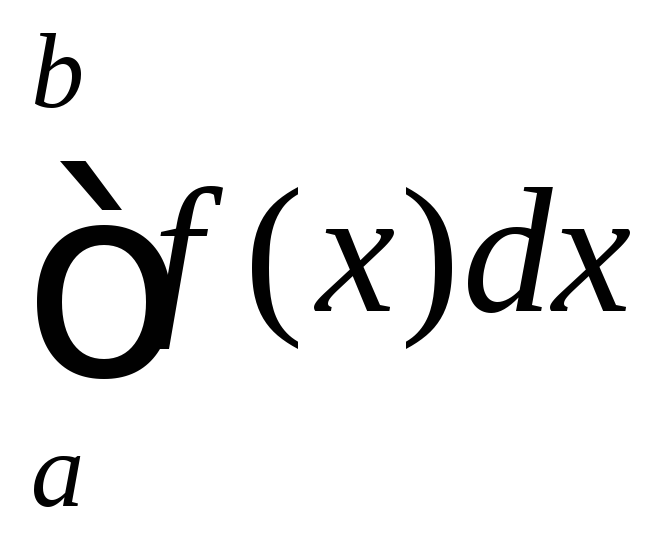 називаютьабсолютно
збіжним.
Якщо ж інтеграл
називаютьабсолютно
збіжним.
Якщо ж інтеграл
 збігається, а
збігається, а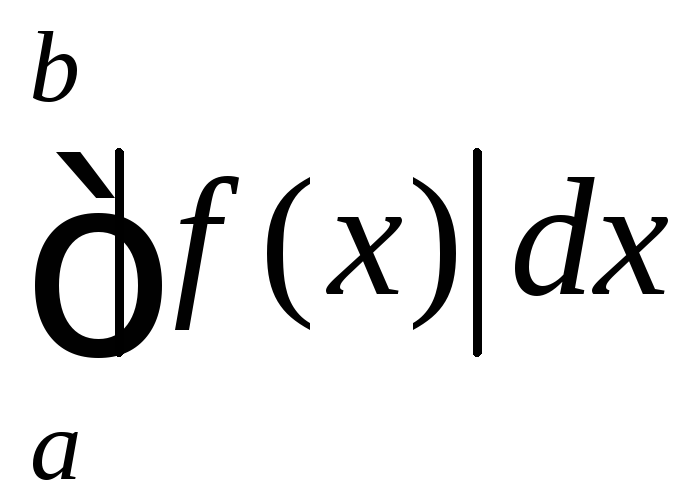 розбігається, то інтеграл
розбігається, то інтеграл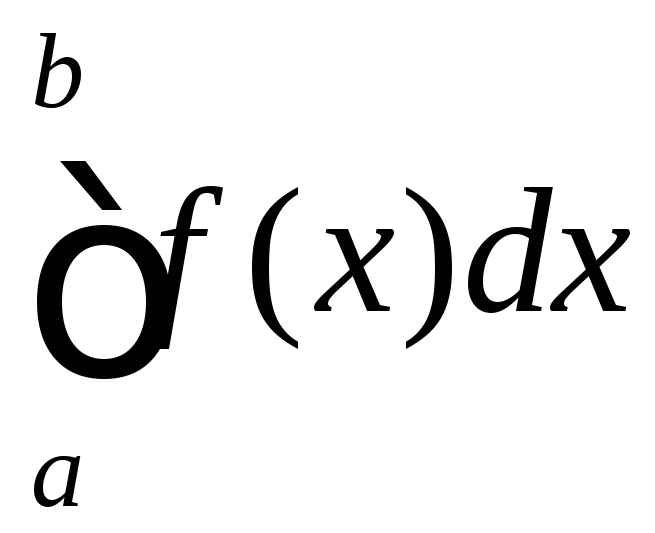 називаютьумовно
(або неабсолютно)
збіжним.
називаютьумовно
(або неабсолютно)
збіжним.
Приклад.
Дослідити на збіжність інтеграл
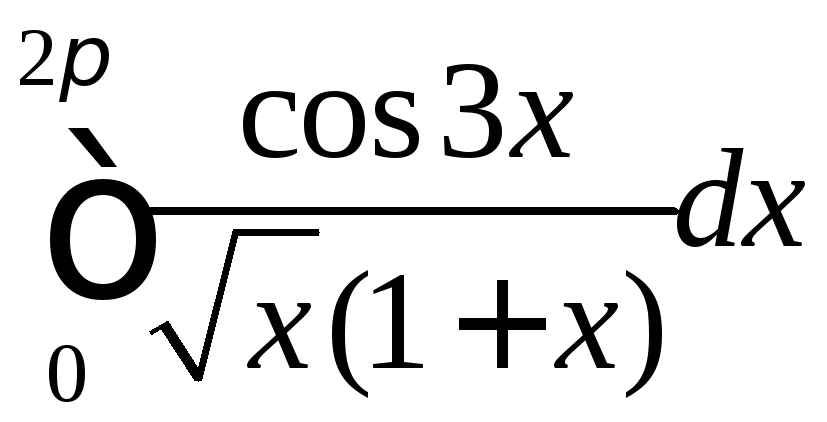 .
Підінтегральна функція має особливу
точку
.
Підінтегральна функція має особливу
точку![]() .
При цьому
.
При цьому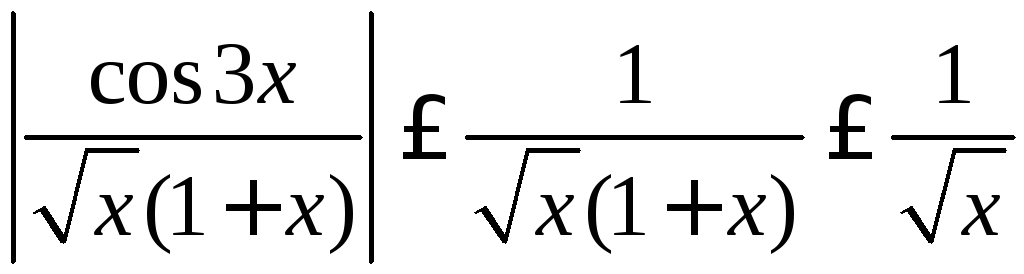 .
Оскілки збігається
.
Оскілки збігається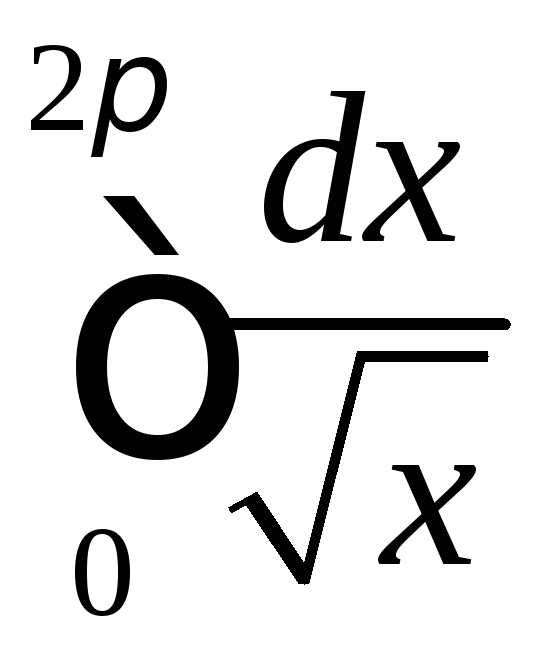 ,
то збігається і
,
то збігається і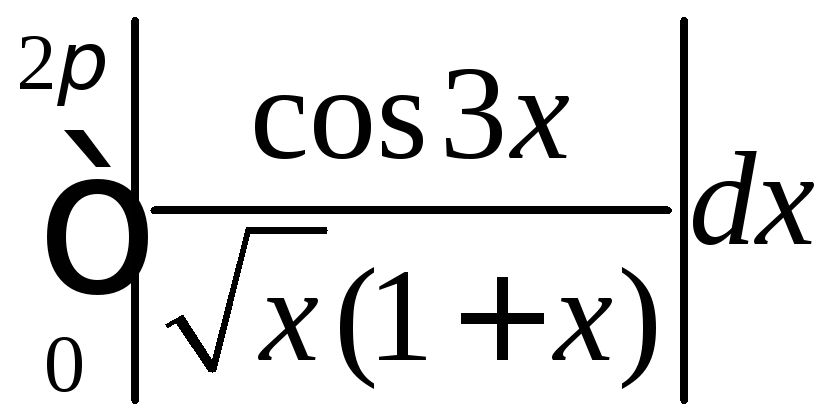 ,
отже збігається (абсолютно) і заданий
інтеграл.
,
отже збігається (абсолютно) і заданий
інтеграл.
27. Наближене обчислення визначених інтегралів
Задачі практики приводять іноді до інтегралів, точне обчислення яких за формулою Ньютона-Лейбніца неможливе або утруднене: первісна підінтегральної функції може не виражатися через елементарні функції, відшукання первісної може вимагати надто громіздких обчислень, нарешті підінтегральна функція може бути задана таблицею чи графіком, а не аналітичним виразом. В таких випадках інтеграл доводиться обчислювати наближено за допомогою чисельних методів. Ми розглянемо тут два такі методи, найпростіші і в той же час широко використовувані як при ручних обчисленнях, так і для програмування на ЕОМ.
Рис. 23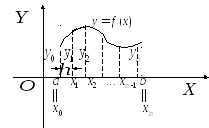
![]()
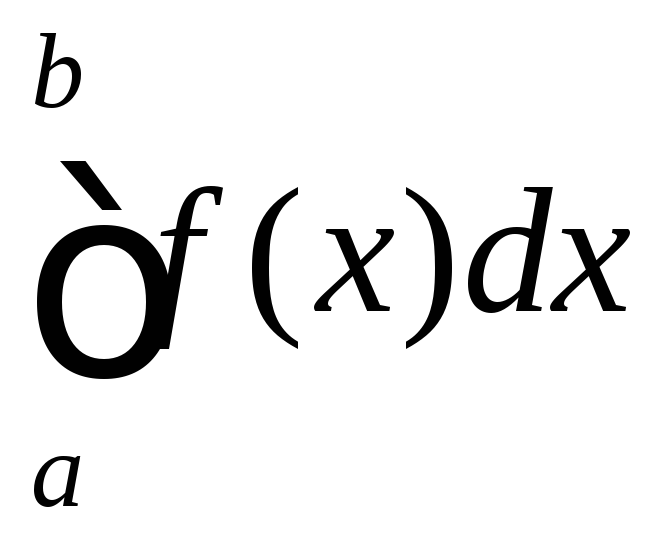 ,
де
,
де![]() неперервна на відрізку
неперервна на відрізку![]() .
Розіб’ємо відрізок
.
Розіб’ємо відрізок![]() на
на![]() рівних частин точками
рівних частин точками![]()
![]() ,
де
,
де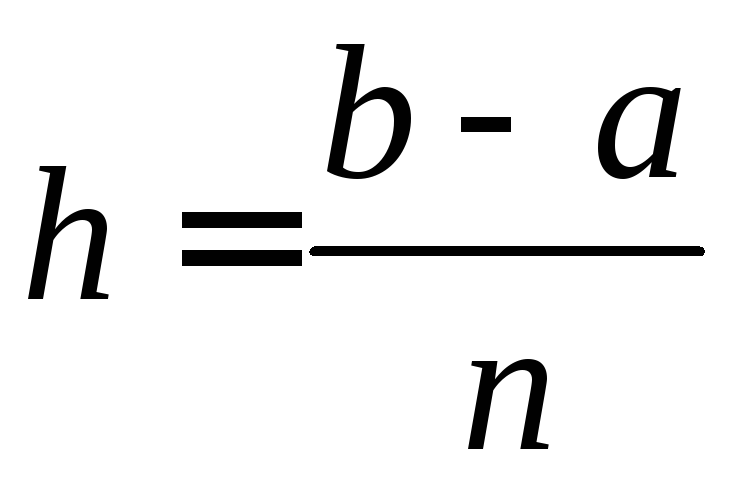 -крок
розбиття
(або
крок
інтегрування).
-крок
розбиття
(або
крок
інтегрування).
Позначимо
![]()
![]() -ординати
графіка
підінтегральної
функції
в точках поділу. Задача полягає в тому,
щоб дати вираз наближеного значення
інтеграла
-ординати
графіка
підінтегральної
функції
в точках поділу. Задача полягає в тому,
щоб дати вираз наближеного значення
інтеграла
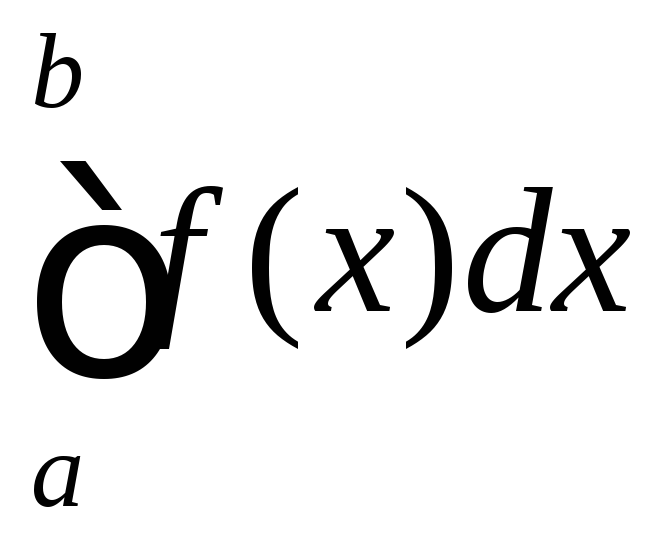 через ці ординати.
через ці ординати.
а
Рис. 23![]()

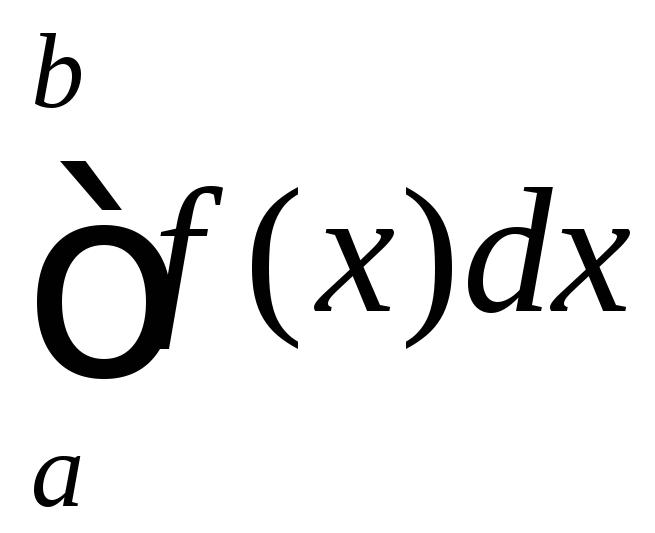 - площа фігури , обмеженої графіком
підінтегральной функції, відрізком
- площа фігури , обмеженої графіком
підінтегральной функції, відрізком![]() і крайніми ординатами
і крайніми ординатами![]() та
та![]() .
Внаслідок виконаного розбиття відрізка
.
Внаслідок виконаного розбиття відрізка![]() ця фігура розбита на
ця фігура розбита на![]() смужок шириною
смужок шириною![]() .
Якщо
.
Якщо![]() достатньо мале, то площу кожної такої
смужки можна вважати наближено
рівною площі
трапеції з висотою
достатньо мале, то площу кожної такої
смужки можна вважати наближено
рівною площі
трапеції з висотою
![]() і основами, які дорівнюють
ординатам, що обмежують
смужку.
і основами, які дорівнюють
ординатам, що обмежують
смужку.
Тоді
площа першої смужки 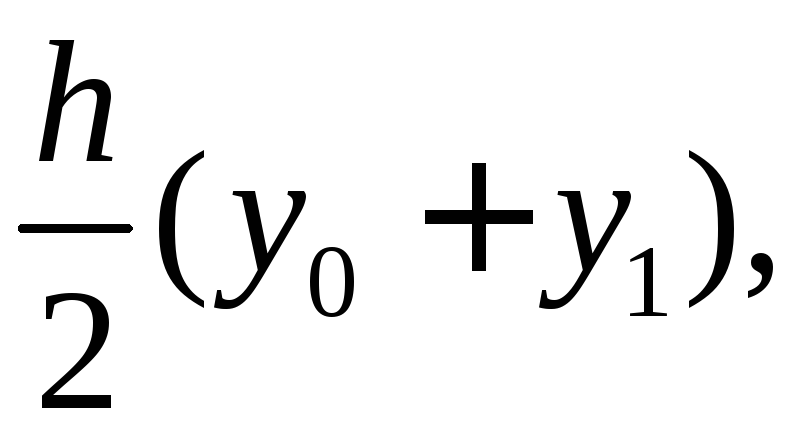 площа другої смужки
площа другої смужки
……
Площа
![]() ої
смужки
ої
смужки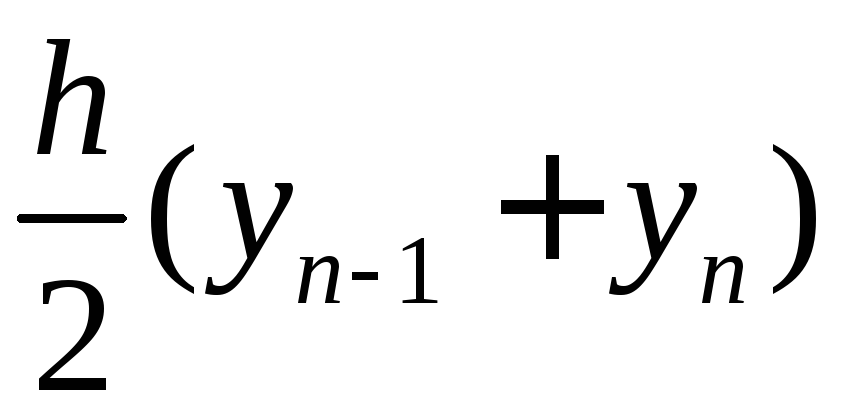 .
.
Додаючи ці площі, отримуємо наближене значення шуканого інтеграла:
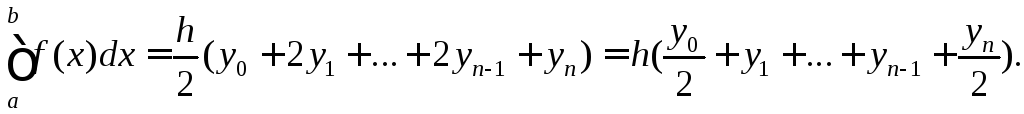
Це
і є правило або формула
трапецій.
Можна довести, що гранична абсолютна
похибка
![]() цієї
формули наближено пропорціональна
цієї
формули наближено пропорціональна![]() ,
тобто
,
тобто![]() Таким чином, при зменшенні кроку
Таким чином, при зменшенні кроку![]() вдвічі похибка зменшується приблизно
в 4 рази. Цим можна скористатися для
наближеної (а для деяких функцій і
точної) оцінки похибки. Для цього
обирають число
вдвічі похибка зменшується приблизно
в 4 рази. Цим можна скористатися для
наближеної (а для деяких функцій і
точної) оцінки похибки. Для цього
обирають число![]() парним
і обчислення інтеграла повторюють з
подвоєним кроком. Нехай
парним
і обчислення інтеграла повторюють з
подвоєним кроком. Нехай![]() -
точне значення інтеграла,
-
точне значення інтеграла,![]() -
результат обчислення з кроком
-
результат обчислення з кроком![]() ,
,![]() -
результат обчислення з кроком
-
результат обчислення з кроком![]() і
і![]() - похибка результата
- похибка результата![]() .
Тоді
.
Тоді![]() ,
звідки одержуємо оцінку
,
звідки одержуємо оцінку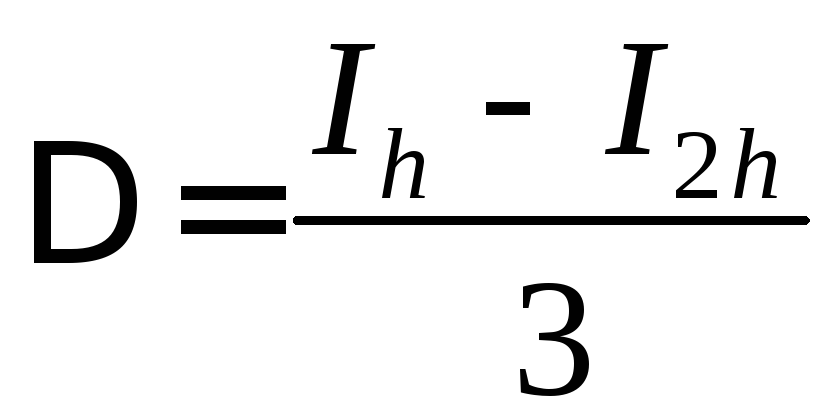 .
.
Приклад.
Розглянемо застосування формули трапецій
на прикладі інтеграла, точне значення
якого відоме
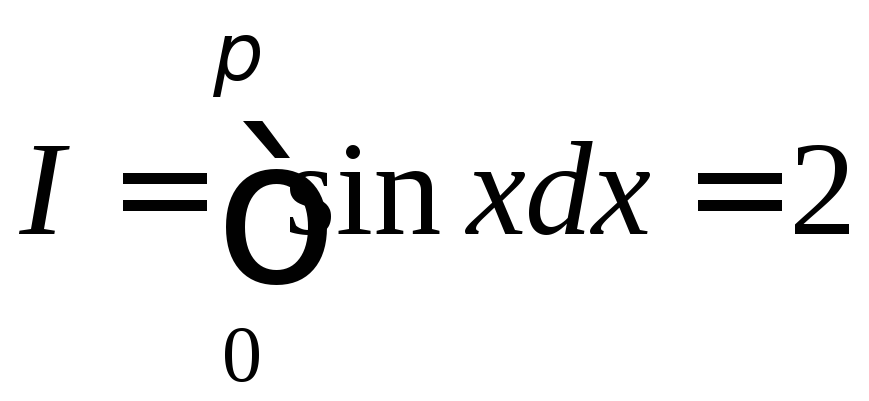 .
Оберемо
.
Оберемо![]() ,
тоді
,
тоді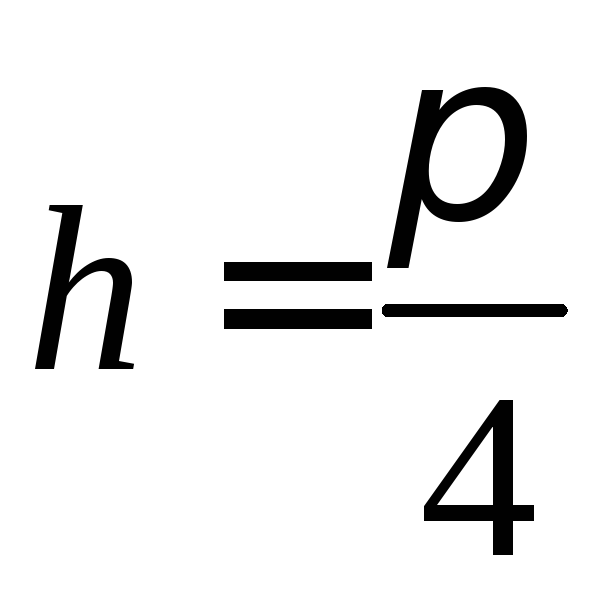 ,
,![]() ,
,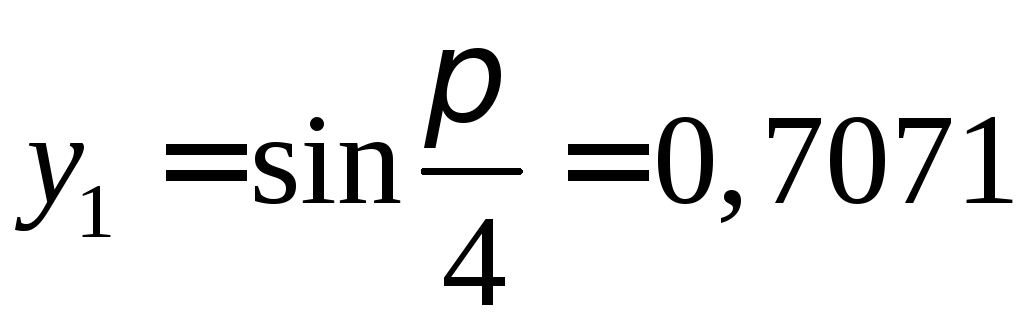 ,
,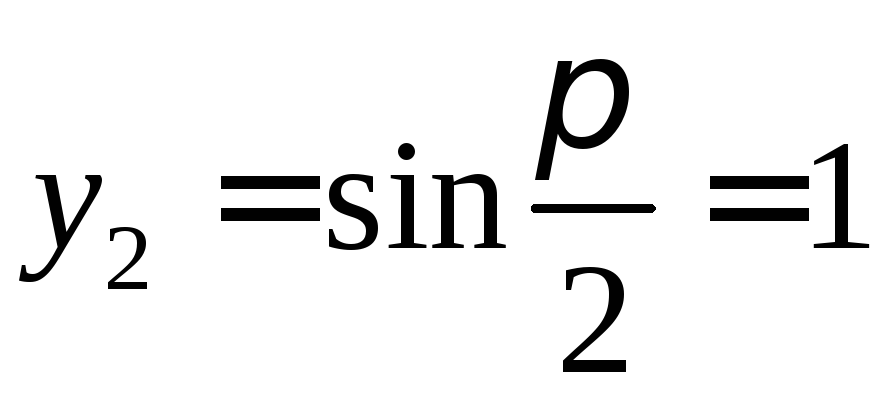 ,
,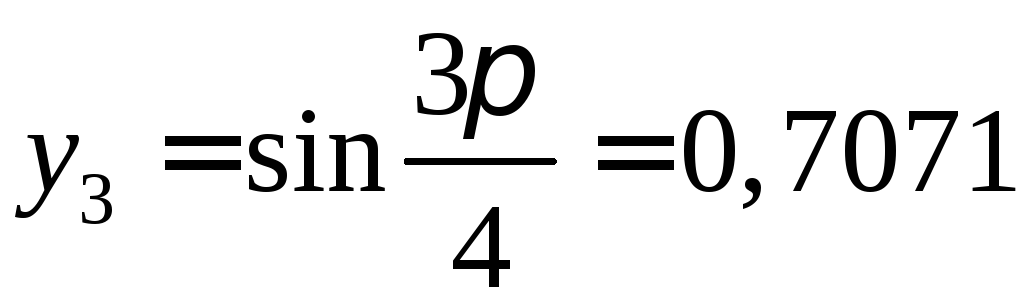 ,
,![]() .
Тоді
.
Тоді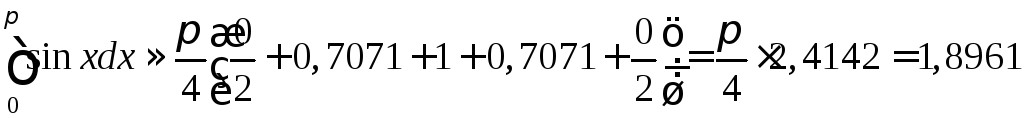 .
Похибка близько
.
Похибка близько![]() ,
тобто близько
,
тобто близько![]() %.
%.
б) Правило Сімпсона (правило парабол).
За
правилом Сімпсона число
![]() береться парним. Позначимо, як і раніше,
через
береться парним. Позначимо, як і раніше,
через![]() -
результат обчислення інтеграла
-
результат обчислення інтеграла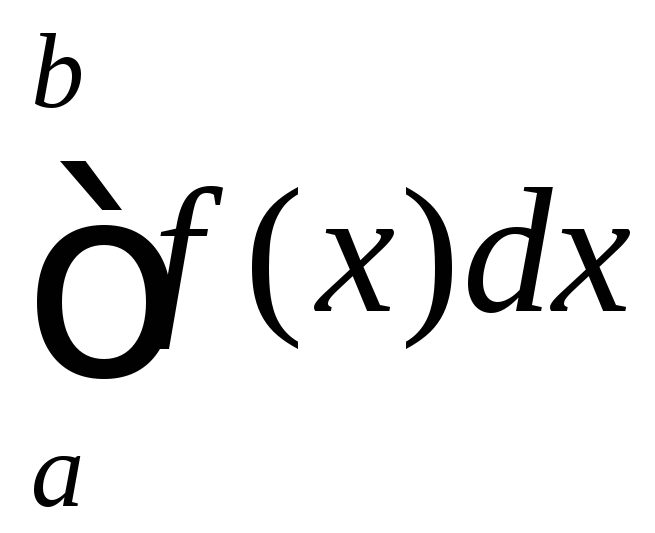 за правилом трапецій з кроком
за правилом трапецій з кроком![]() ,
а
,
а![]() -
теж саме з подвоєним кроком. Для похибки
результату
-
теж саме з подвоєним кроком. Для похибки
результату![]() було одержано вираз
було одержано вираз .
Якщо до
.
Якщо до![]() додати цю похибку, то результат очевидно
стане точнішим. Тому природно покласти
додати цю похибку, то результат очевидно
стане точнішим. Тому природно покласти

Замінимо
![]() і
і![]() їх виразами:
їх виразами:
![]()
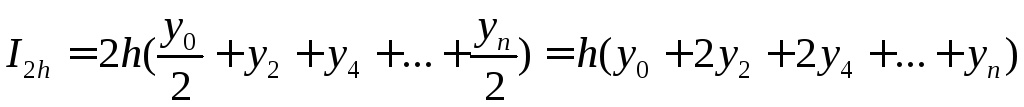 .
.
Тоді
![]()
![]() ,
,
звідки отримуємо
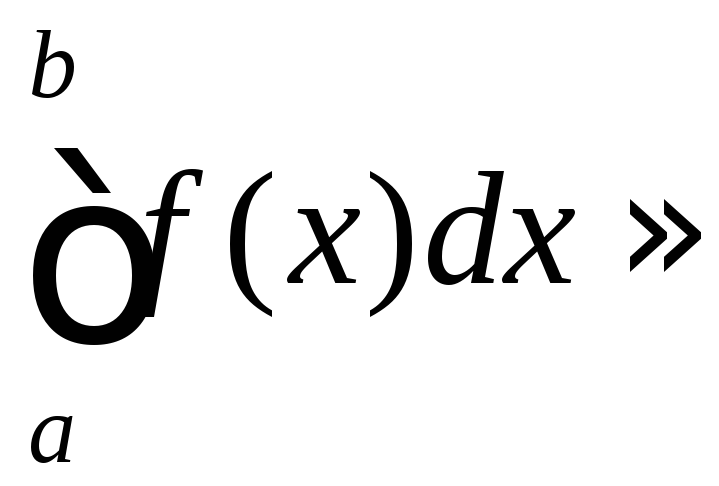
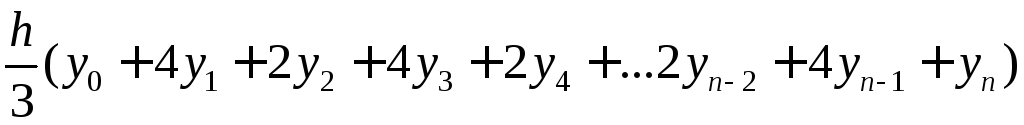 .
.
Це і є
формула Сімпсона. Її називають також
формулою парабол, тому що її можна
отримати подібно до формули трапецій,
але замінюючи на кожній парі частинних
відрізків графік функції
![]() параболою, яка проходить через ті ж
точки (а не ламаною, як у методі трапецій).
Правило Сімпсона при незначному
збільшенні обсягу обчислень значно
точніше, ніж правило трапецій. Його
гранична похибка
параболою, яка проходить через ті ж
точки (а не ламаною, як у методі трапецій).
Правило Сімпсона при незначному
збільшенні обсягу обчислень значно
точніше, ніж правило трапецій. Його
гранична похибка![]() наближено пропорціональна
наближено пропорціональна![]() ,
тобто
,
тобто![]() ,
і при зменшенні кроку в 2 рази зменшується
в 16 разів.
,
і при зменшенні кроку в 2 рази зменшується
в 16 разів.
Приклад.
Розглянемо знову
 і оберемо, як і в попередньому прикладі,
і оберемо, як і в попередньому прикладі,![]() .
Тоді
.
Тоді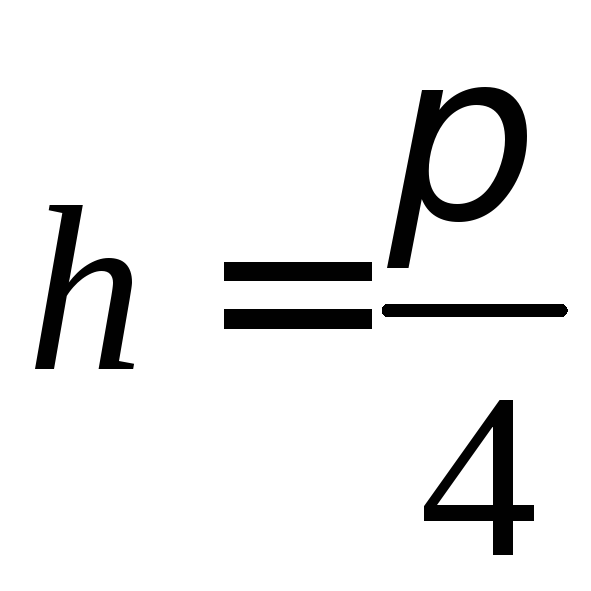 ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
За формулою Сімпсона

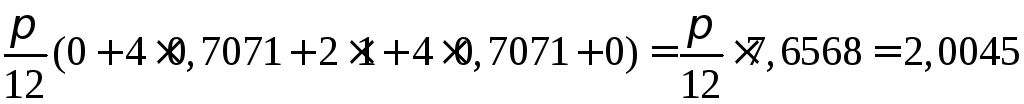 .
.
Похибка близько 0,0045, тобто близько 0,23% і порівняно з похибкою правила трапецій менша в 22 рази.
