Тема III: Взаимный базис, ковариантные и контравариантные компоненты вектора.

Основные формулы:

–определение взаимного базиса rⁱ

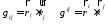–фундаментальная матрица.

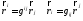
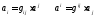
I. Цилиндрическая система координат

Определим элементы фундаментальной матрицы, для этого составим скалярные произведения векторов локального базиса.

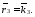
и

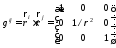
Матрица g^ij определена как обратная к матрице g_ij. Это было доказано в лекции. Матрица диагонального вида, следовательно, цилиндрическая система координат это ортогональная криволинейная система координат. Найдем векторы взаимного базиса для этой системы координат.

II. Сферическая система координат

Определим элементы фундаментальной матрицы, для этого составим скалярные произведения векторов локального базиса.

Матрица g^ij определена как обратная к матрице g_ij. Фундаментальная матрица диагонального вида, следовательно, сферическая система координат это ортогональная криволинейная система координат. Найдем векторы взаимного базиса для этой системы координат.

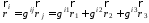
Задача 1. Известны контравариантные компоненты вектора в точкецилиндрической системы координат. Найдите ковариантные компоненты этого вектора в точкеМ.

Решение. Для нахождения ковариантных компонент вектора воспользуемся формулой

тогда получим

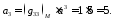
^Ответ:

Задача 2. Известны координаты вектора а в декартовой прямоугольной системе координат 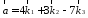. Найдите ковариантные и контравариантные компоненты этого вектора в точке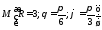сферической системы координат.

Решение.

Определим векторы локального базиса в точке М сферической системы координат

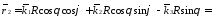
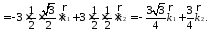
Найдем ковариантные компоненты вектора в точке М, как скалярные произведения данного вектора на базисные векторы.

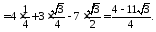
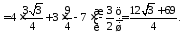
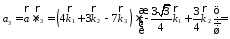
Найдем контравариантные компоненты вектора в точке М с помощью фундаментальной матрицы и найденных ковариантных компонент вектора.

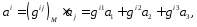
где

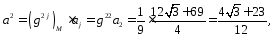
^Ответ:

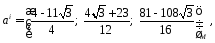
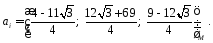
Тема IV. Определение тензора

Определение. Экстенсив Q называется m-раз ковариантным и n-раз контравариантным тензором ранга m+n, если его компоненты преобразуются по закону

где –матрицы Якоби преобразования криволинейных координат.

Задача 1. Задан смешанный тензор второго ранга

и матрица прямого преобразования криволинейных координат

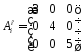. Найдите тензор в новых осях.

Решение. Запишем определение смешанного тензора второго ранга, т.е. закон преобразования его компонент при переходе к новой системе координат

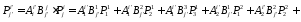
Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим

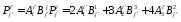
Найдем матрицу обратного преобразования координат, как матрицу обратную к матрице прямого преобразования координат

Определим компоненты тензора в «новых» осях

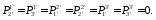
Ответ:

Замечание. Для дважды ковариантного тензора второго ранга и дважды контравариантного тензора второго ранга используются следующие законы преобразования

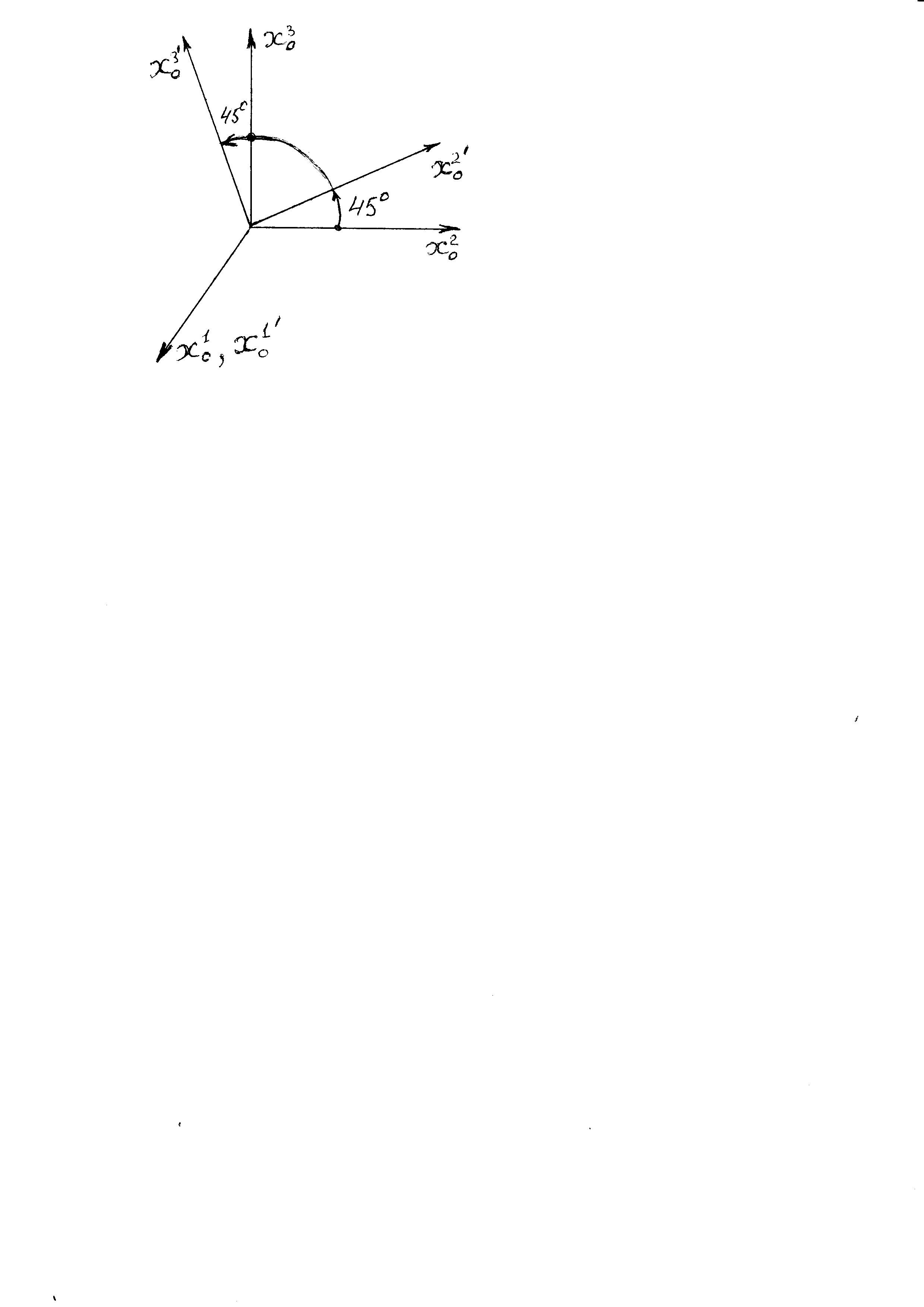
Задача 2. Задан декартов тензор второго ранга Найдите тензор в новых осях, полученных путем поворота старых на угол 45⁰ относительно оси .

Решение. Определим матрицу преобразования декартовых координат – это матрица косинусов углов межу новыми и старыми осями

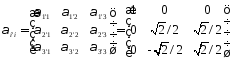
Запишем определение декартового тензора второго ранга

Подставим компоненты тензора в «старых» осях из условия задачи, тогда получим

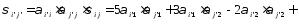
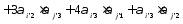
Определим компоненты тензора в «новых» осях

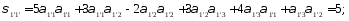
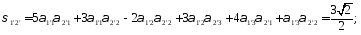
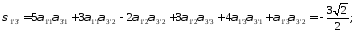
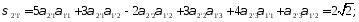
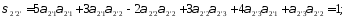
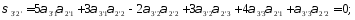
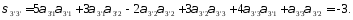
Ответ:

Замечание. В этой задаче важно правильно составить матрицу преобразования декартовых координат при одном повороте относительно других осей . Следует рассмотреть отдельно углы поворота осей 90⁰ и 180⁰.