ИДЗ по бодрякову

ФГБОУ ВПО Уральский государственный педагогический университет

Математический факультет

В.Ю. Бодряков

Индивидуальные домашние задания (ИДЗ)

по дисциплине «Математика»

Часть 1

Екатеринбург – 2014

Введение

Настоящая методическая разработка предназначена для студентов всех форм обучения, изучающих дисциплину «Математика». Разработка содержит индивидуальные домашние задания (ИДЗ) по 30 вариантов в каждом и методические указания к их решению.

Методические указания к решению задач

ИДЗ-1. Основные понятия теории множеств

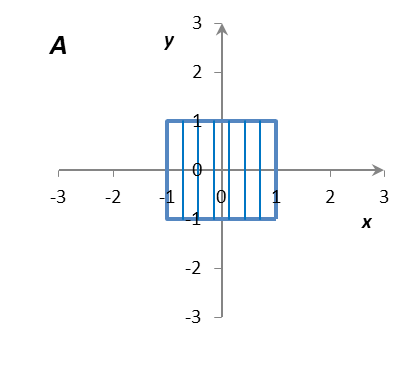
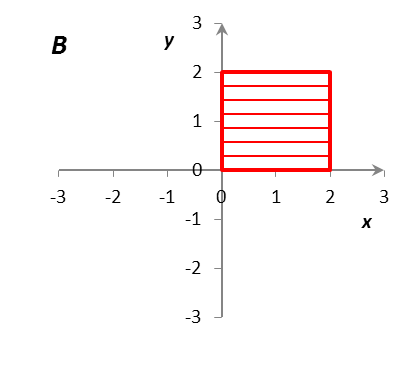
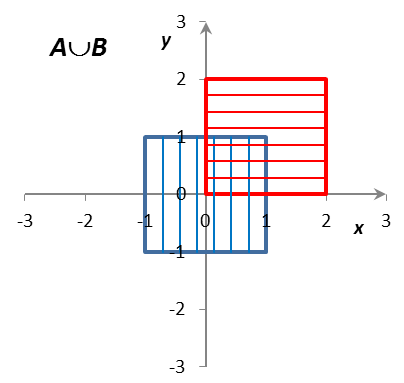
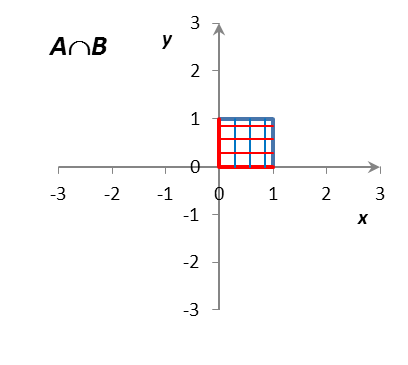
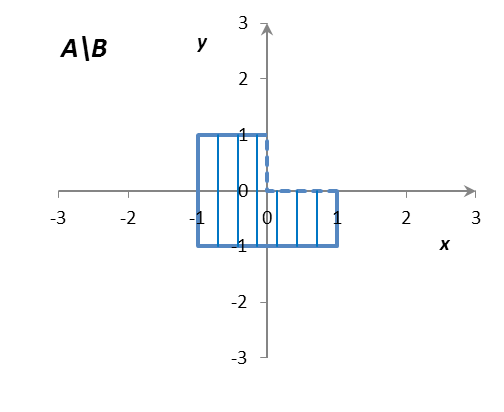
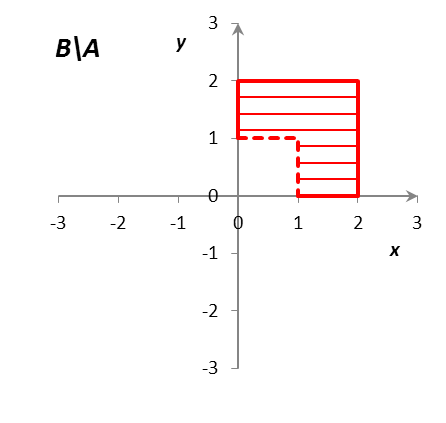
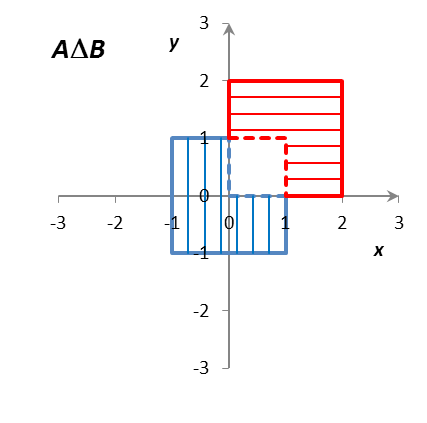
Определить и изобразить на рисунках множества A, B, AB, AB, A/B, B/A, AB, где

A = {(x, y)  R²: |x|  1, |y|  1},

B = {(x, y)  R²: |x – 1|  1, |y – 1|  1}.

Решение: Множества A и B представляют собой множества точек на декартовой плоскости R  R = R² (плоскости Oxy). Как нетрудно установить, множество A представляет собой внутренность квадрата с центром в точке (0; 0) со сторонами длиной 2, параллельными координатным осям; граница принадлежит множеству A. Аналогично, множество B представляет собой внутренность квадрата с центром в точке (1; 1) со сторонами длиной 2, параллельными координатным осям; граница принадлежит множеству B. Множества A, B, AB, AB, A/B, B/A, AB изображены на рис. 1.

ИДЗ-2. Законы алгебры множеств

Пусть A, B, C – подмножества некоторого универсального множества U. Установите справедливость нижеследующего утверждения:

(A\B)(B\A) = (AB)\(AB).

Решение: Разложим множества A и B на непересекающиеся подмножества {x_A}, {x_B}, {x_AB}:

A = {x_Ax_AB};

B = {x_Bx_AB}.

В этих обозначениях для левой части предполагаемого равенства имеем:

A\B = {x_Ax_AB}\{x_Bx_AB} = {x_A};

B\A = {x_Bx_AB}\{x_Ax_AB} = {x_B};

(A\B)(B\A) = {x_A}{x_B} = {x_Ax_B}.

Для правой части равенства имеем:

AB = {x_Ax_AB}{x_Bx_AB} = {x_Ax_Bx_AB};

AB = {x_Ax_AB}{x_Bx_AB} = {x_AB};

(AB)\(AB) = {x_Ax_Bx_AB}\{x_AB} = {x_Ax_B}.

Левая и правая части доказываемого равенства одинаковы и равны {x_Ax_B}. Справедливость утверждения установлена.

	Рис. 1

ИДЗ-3. Элементы комбинаторики

а) Вычислите значение X комбинаторного выражения;

б) Решите комбинаторную задачу;

в) Решите комбинаторную задачу повышенного уровня сложности.

а) X = 10P₄ – ;

б) В студенческой группе 10 девушек и 6 юношей. Для участия в эстафете от группы требуется выставить команду из двух девушек и двух юношей. Сколькими способами можно сформировать команду?

в) Сколькими способами шесть пассажиров могут сесть в электричку из пяти вагонов так, чтобы ни один вагон не оставался пустым?

Решение: 1а) С учетом известных формул комбинаторики (без повторений) для числа перестановок из n элементов:

P_n = n!;

размещений из n элементов по k элементов:

= ;

и сочетаний из n элементов по k элементов:

= ;

проведем необходимые преобразования:

X = 10P₄ – = 104! – = 25!  – 5! =

= 5!(2 – 1) = 5! = 120.

б) Число способов выбрать для участия в команде двух девушек равно:

= = = 45.

Аналогично, число способов выбрать для участия в команде двух юношей равно:

= = = 15.

Согласно комбинаторному принципу умножения, число способов сформировать команду из двух девушек и двух юношей равно:

n =  = 4515 = 675.

в) Из условия задачи ясно, что в одном вагоне (из пяти) должны разместиться два пассажира, а в остальных четырех вагонах – по одному.

Для удобства будем считать, что вначале в один из вагонов электрички садятся два человека, отобранных из шести, а затем оставшиеся четыре человека рассаживаются по одному в оставшиеся четыре вагона.

Число способов выбрать два пассажира из шести составляет = 15. Число способов этой паре пассажиров разместиться в одном из пяти вагонов равно числу вагонов, т.е. 5. Таким образом, число способов двум пассажирам, отобранным из шести, разместиться парой в пяти вагонах, равно  5 = 155 = 75. Оставшиеся четыре человека могут разместиться по одному в четырех вагонов числом способов равны числу перестановок из четырех: P₄ = 4! = 24.

Окончательно, полное число способов шести пассажирам сесть в электричку из пяти вагонов так, чтобы ни один вагон не оставался пустым, составляет n = 5P₄ = 7524 = 1800.

Ответ: a) X = 120; б) n =  = 675; в) n = 5P₅ = 1800.

ИДЗ-4. Классическое определение вероятности

Решите задачу на вычисление вероятности, основываясь на ее классическом определении.

Из множества всех последовательностей длины 10, состоящих из цифр 0; 1; 2; 3, наудачу выбирается одна. Какова вероятность того, что выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности.

Решение: Вероятность события A – «Выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности», согласно классическому определению, равна

P(A) = ,

где n – полное число равновероятных исходов; m – число исходов, благоприятствующих событию A.

Число способов заполнить 10 позиций в последовательности цифрами 0; 1; 2; 3 составляет, с учетом возможности повторения цифр,

n = 4¹⁰ = 2²⁰ = 1048576.

Число способов разместить 5 нулей на 10 позициях в последовательности при условии, что нули обязательно находятся на первом и десятом месте в последовательности, равно числу способов разместить три нуля на восьми свободных позициях в последовательности и равно числу сочетаний из 8 элементов по 3: = = 56. Оставшиеся 8 – 3 = 5 позиций в последовательности будут заполнены цифрами 1; 2; 3. Число способов осуществить это, с учетом возможности повторения, равно 3⁵ = 243. Т.о., число исходов, благоприятствующих событию A, равно

m = 3⁵ = 56243 = 13608.

Искомая вероятность события A равна:

P(A) = = 0,013.

Ответ: P(A) = = 0,013.

Варианты индивидуальных домашних заданий (ИДЗ)

ИДЗ-1. Основные понятия теории множеств

Определить и изобразить на рисунках множества A, B, AB, AB, A/B, B/A, AB:

1. A = {(x, y)  R²: x  y}, B = {(x, y)  R²: |x| + |y|  1};

2. A = {(x, y)  R²: y  –x}, B = {(x, y)  R²: x² + y²  1};

3. A = {(x, y)  R²: y  x²}, B = {(x, y)  R² : x² + (y – 1)²  1};

4. A = {(x, y)  R²: xy  0}, B = {(x ,y)  R²: x² + y²  1};

5. A = {(x, y)  R²: y  –x²}, B ={(x, y)  R²: (x + 1)² + (y + 1)²  1};

6. A = {(x, y)  R²: xy  0}, B ={(x, y)  R²: |x| + |y|  1};

7. A = {(x, y)  R²: x  y}, B = {(x, y)  R²: 9x² + y²  36};

8. A = {(x, y)  R²: x  y}, B ={(x, y)  R²: 4x² + 9y²  36};

9. A = {(x, y)  R²: max{|x|, |y|}  1}, B = {(x, y)  R²: x² + y²  1};

10. A = {(x, y)  R²: max{|x|, |y|}  2}, B= {(x, y)  R²: y  x + 1};

11. A = {(x, y)  R²: y  x²}, B = {(x, y)  R²: y  4 – x²};

12. A = {(x, y)  R²: x  –y}, B = {(x, y)  R² : |x| + |y|  2};

13. A ={(x, y)  R²: |x| + |y|  3}, B = {(x, y)  R²: max{|x|, |y|}  2};

14. A = {(x, y)  R²: y  –x²}, B = {(x, y)  R²: (x – 1)² + (y + 1)²  1};

15. A = {(x, y)  R²: xy  0}, B = {(x, y)  R²: x² + (y + 1)²  1};

16. A = {(x, y)  R²: xy  0}, B = {(x, y)  R²: x² + y²  4};

17. A = {(x, y)  R²: y  x²}, B = {(x, y)  R²: (x – 1)² + (y + 1)²  4};

18. A = {(x, y)  R²: x²  y}, B = {(x, y)  R²: x² + y²  4};

19. A = {(x, y)  R²: xy  0}, B = {(x, y)  R²: |x| + |y – 2|  1};

20. A = {(x, y)  R²: x  –y}, B = {(x, y)  R²: (x – 2)² + (y + 3)²  1};

21. A = {(x, y)  R²: x  y}, B = {(x, y)  R² : 9x² + y²  9};

22. A = {(x, y)  R²: x  y}, B = {(x, y)  R²: x² + 4y²  4};

23. A = {(x, y)  R²: |x| + |y|  2}, B = {(x, y)  R²: 9x² + y²  9};

24. A = {(x, y)  R²: max{|x|, |y|}  2}, B = {(x, y)  R²: x² + 1  y};

25. A = {(x, y)  R²: max{|x|, |y|}  2}, B = {(x, y)  R²: 4 – x²  y};

26. A = {(x, y)  R²: xy  1}, B = {(x, y)  R² : x² + y²  9};

27. A = {(x, y)  R²: x² + y²  4}, B = {(x, y)  R²: (x + 1)² + (y + 1)²  4};

28. A = {(x, y)  R²: |x| + |y|  4}, B = {(x, y)  R²: x² + y²  16};

29. A = {(x, y)  R²: y  (x – 2)²}, B = {(x, y)  R²: x² + y²  4};

30. A = {(x, y)  R²: x + y  3}, B = {(x, y)  R²: (x – 1)² + (y – 1)²  9}.

ИДЗ-2. Законы алгебры множеств

Пусть A, B, C – подмножества некоторого универсального множества U. Установите справедливость нижеследующих утверждений.

1. (U\B)\(U\A)  A\B; 2. (U\A)\B = U\(AB);

3. A\C  (A\B)(B\C); 4. (AB)C = (AC)(BC);

5. Если A  B, то U\B  U\A; 6. AB = U\((U\A)(U\B));

7. AB = A(AB); 8. A\B = A(AB);

9. Если AB = A, то B = ; 10. (AB)C  (AC)(BC);

11. (AB)(BC) = (ABC)\(ABC); 12. AB = (U\A)(U\B);

13. A(AB) = B; 14. (A\C)\(B\A)  A\C;

15. (A\C)\(B\A)  (A\B)(B\C); 16. (A\C)  (A\B)(B\C);

17. Если U\B  U\A, то A  B; 18. A(BC) = (AB)(AC);

19. AB  (AС)( BC); 20. A\(B\C) = (A\B)(AC);

21. (A\B)\C = (A\C)\(B\C); 22. (AB)\C = (A\C)(B\C);

23. Если C  A, то A\(B\C) = (A\B)C; 24. (AB)\C = (A\C)(B\C);

25. (A\B)C = (AC)\B; 26. (A\B)C  (AC)\B;

27. (AB)\C = (A\C)(B\C); 28. (A\B)\(A\C) = (AC)\(AB);

29. (AB)\C = (A\(BC))(B\(AC)); 30. (A\B)C = (AC)\(BC).

ИДЗ-3. Элементы комбинаторики

а) Вычислите значение X комбинаторного выражения;

б) Решите комбинаторную задачу;

в) Решите комбинаторную задачу повышенного уровня сложности.

1. а) X = – ;

б) На конференции должны выступить 7 докладчиков. Сколькими способами можно составить списки выступлений ораторов?

в) Сколькими способами можно выбрать из колоды в 36 карт пять карт так, чтобы среди них было не менее трех шестерок?

2. а) X = – ;

б) Сколько пятизначных телефонных номеров, в которых цифры не повторяются, можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8?

в) Имеются 5 путевок в Турцию и 7 – в Грецию. Сколькими способами можно отправить 9 туристов на отдых в Турцию или Грецию?

3. а) X = – ;

б) На книжной полке стоят 12 книг различных авторов. Сколькими способами можно взять с полки 7 книг?

в) Сколько различных трехбуквенных слов, в которых буквы не повторяются и есть только одна гласная буква, можно составить из букв а, б, в, г, е, ж?

4. а) X = – ;

б) Сколькими способами можно опустить 4 различных письма в 10 почтовых ящиков, если в каждый ящик опускают не более одного письма?

в) Сколькими способами можно переставить буквы в слове «высота» так, чтобы все согласные стояли рядом?

5. а) X = + 2;

б) Сколькими способами могут быть распределены 5 контрамарок (билетов без указания места) на спектакль среди 12 учеников класса?

в) Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6 так, чтобы каждое из этих чисел начиналось и заканчивалось четной цифрой?

6. а) X = + 2P₅;

б) Сколькими способами можно расположить на книжной полке 7 различных книг?

в) Сколькими способами можно выбрать из колоды в 36 карт четыре карты так, чтобы ровно три из них были одной масти?

7. а) X = + ;

б) У студента имеется 7 различных учебников. Сколькими способами можно выбрать 3 учебника?

в) Сколькими способами можно расставить на книжной полке 8 томов собрания сочинений так, чтобы первый, второй и третий тома стояли рядом?

8. а) X = 5 – ;

б) Сколько трехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6?

в) Сколькими способами можно выбрать из колоды в 36 карт пять карт так, чтобы среди них точно была одна шестерка и одна семерка, причем одной масти?

9. а) X = – ;

б) Сколькими способами можно усадить на скамейку 6 человек?

в) В спортивной секции занимаются 10 человек. Сколькими способами можно выбрать из них 5 человек, среди которых трое – участники эстафеты 100 + 400 + 500 и двое – запасных?

10. а) X = + ;

б) Сколькими способами можно выбрать из колоды в 36 карт две карты: одну масти «крести», другую – масти «черви»?

в) На школьной конференции от класса в 20 чел. должны участвовать 5 представителей; среди них – 2 докладчика: по математике и по истории. Сколькими способами можно составить команду участников?

11. а) X = + ;

б) На вершину горы ведут 5 троп. Сколькими способами два туриста, идущие разными тропами, могут добрать до вершины?

в) Из студенческой группы, в которой 7 юношей и 9 девушек, нужно выбрать трех дежурных так, чтобы среди них были и юноши и девушки. Сколькими способами это можно сделать?

12. а) X = 5 – ;

б) У одного школьника 10 различных значков, а у другого 8 различных календариков. Сколькими способами можно обменять 1 значок на один календарик?

в) В ящике лежат 2 черных и 8 белых шаров. Сколькими способами можно извлечь из ящика 5 шаров так, чтобы среди них имелись черные шары?

13. а) X = – 7;

б) Сколько трехбуквенных слов, в которых буквы не повторяются, можно составить из букв слова «медиана»?

в) Сколькими способами можно переставить цифры в числе 1234567 так, чтобы в результате перестановки все четные цифры стояли рядом?

14. а) X = + ;

б) Сколькими способами можно распределить 7 лотерейных билетов среди 12 школьников так, чтобы каждому досталось не более одного билета?

в) Сколькими способами можно разложить 10 различных писем в два почтовых ящика так, чтобы в один из них попало не более двух писем, а в другой – все остальные?

15. а) X = 4 + ;

б) Сколько двузначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7?

в) В расписание занятий на субботу можно ставить любой из девяти предметов, среди которых есть алгебра и физика. Сколькими способами можно составить расписание занятий на день, если в данный день должно быть 4 различных урока, включая алгебру и физику, причем последние не должны непосредственно следовать друг за другом?

16. а) X = 20 – P₄;

б) Сколькими способами из 8 бегунов можно выбрать трех участников эстафеты 100 + 400 + 500?

в) Сколько пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 9 так, чтобы в каждом числе были две различные четные цифры и три различные нечетные цифры, причем число начиналось и заканчивалось бы нечетной цифрой?

17. а) X = + ;

б) Из пункта A в пункт B ведут четыре дороги. Сколькими способами турист может добраться из A в B и вернуться обратно?

в) Сколькими способами можно выбрать из колоды в 36 карт четыре карты так, чтобы среди них было не менее двух королей?

18. а) X = – 9;

б) От студенческой группы в 22 чел. Нужно выбрать одного студента для участия в олимпиаде по математике и одного для участия в олимпиаде по физике. Сколькими способами можно сделать этот выбор?

в) В корзине лежат 6 яблок и 7 груш. Сколькими способами можно выбрать 5 фруктов так, чтобы среди них было более трех яблок?

19. а) X = ;

б) Сколько двузначных чисел, оканчивающихся четной цифрой, можно составить из цифр 1, 2, 3, 4, 5, 6, 7?

в) Сколькими способами можно выбрать из колоды в 36 карт шесть карт так, чтобы среди них были точно один туз и один король, причем одной масти?

20. а) X = + 88;

б) Сколько четырехбуквенных слов, в которых буквы не повторяются можно составить из букв слова «директор»?

в) На книжной полке стоят 5 различных книг в сером переплете и 6 различных книг в черном переплете. Сколькими способами можно взять с полки 3 книги так, чтобы среди них были книги в разных переплетах?

21. а) X = 6 + 5;

б) На собрании, где присутствуют 15 чел., должны выступить 4 чел. Сколькими способами можно составить список выступлений ораторов?