Osnovanija_geometrii_OZO

Получим две модели АТ Т, а так как по условию любые две модели изоморфны, то в любой из них имеют место предложения А и А. Полученное противоречие завершает доказательство.

§3. Основные системы аксиом геометрии

3.1. Аксиоматика Гильберта

Давид Гильберт (Hilbert) – нем. математик (1862-1943)

Логик, философ, руководитель одного из основных центров мировой математической науки первой трети 20 в. — Геттингенской математической школы, исследования которой оказали определяющее влияние на развитие математических наук.

В научных исследованиях Гильберта можно четко выделить периоды, посвященные работе в какой-либо одной области математики: а) теория инвариантов (1885–93), б) теория алгебраических чисел (1893–98), в) основания геометрии (1898–1902), г) принцип Дирихле и примыкающие к нему проблемы вариационного исчисления и дифференциальных уравнений (1900–06), д) теория интегральных уравнений (1900–10), е) решение проблемы Варинга в теории чисел (1908–09), ж) основы математической физики (1910– 22), з) логической основы математики (1922–39).

Аксиоматика 1899 г.

3.1.1. Роль аксиоматики Гильберта

Евклид в "Началах" наметил идеал строгого логического изложения геометрии, но не смог до конца выполнить свой замысел, согласно которому необходимо строго отделить минимум того, что должно быть заимствовано и абстрагировано из опыта и геометрической интуиции, и ясно и четко высказано в аксиомах, а далее, без обращений к очевидности и опыту выведены из аксиом определенные факты.

При строгом логическом построении теории в понятиях и аксиомах должны найти своё выражение лишь те свойства и отношения объектов, которые существенны для логических рассуждений. Все остальные признаки должны быть оставлены, как не имеющие значения для дедукции.

Но наши геометрические понятия часто срастаются с их наглядными конкретными представлениями, т.е. существенные свойства сливаются со многими другими несущественными свойствами, что затрудняет выделение существенных признаков.

До Гильберта под аксиомами геометрии понимались совершенно конкретные истины, относящиеся к вполне определенным конкретным объектам – точкам, прямым, плоскостям..., которые связаны с вполне определенными пространственными представлениями. Для Гильберта основные понятия геометрии не связываются ни с какими объектами, они вводятся без прямых определений и всё, что о них необходимо знать, излагается в аксиомах (которые являются как бы косвенными определениями).

Такое построение теории приводит к возможности различных истолкований одной и той же геометрии. Существует как бы "логический скелет", который может быть заполнен различным конкретным материалом. Таким образом, расширяется область приложений геометрии. Её утверждения имеют более общее значение и остаются в силе и для многих объектов, качественно отличающихся от объектов, связанных с обычными геометрическими представлениями.

11

Именно на основе аксиоматики Гильберта строятся аксиоматики различных школьных курсов.

3.1.2. Аксиоматика Гильберта (модифицированная)

Основные объекты: точка, прямая, плоскость Основные отношения: принадлежать, лежать между, конгруэнтность (равенство) Структура аксиоматики (5 групп):

I. Аксиомы принадлежности (8) II. Аксиомы порядка (4)

III. Аксиомы конгруэнтности (5)

IV. Аксиомы непрерывности (2) V. Аксиома параллельности

Замечание. У самого Гильберта аксиома параллельности составляет 4 группу, а аксиомы непрерывности – 5-ю.

I. Аксиомы принадлежности

I1. Для любых двух точек А и В существует прямая, которой принадлежит каждая из

них.

I2. Существует не более одной прямой, проходящей через каждую из двух данных точек А и В.

Теорема 1. Через любые две точки проходит одна и только одна прямая

I3. На всякой прямой существуют по крайней мере две точки. Существуют по крайней мере 3 точки, не принадлежащие одной прямой.

I4. Для любых трех точек А, В, С, не лежащих на одной прямой, существует плоскость, которая проходит через каждую из трех точек А, В и С. Каждой плоскости принадлежит по меньшей мере одна точка.

I5. Для любых трех точек, не лежащих на одной прямой, существует не более одной плоскости, проходящей через эти точки.

Теорема 2. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

I6. Если две точки А и В прямой а лежат в плоскости П, то всякая точка прямой а лежит в плоскости П.

Замечание. В этом случае говорят, что прямая а лежит в плоскости П или плоскость П проходит через прямую а.

I7. Если две плоскости П1 и П2 имеют общую точку А, то они имеют по крайней мере еще одну общую точку В.

I8. Существует по крайней мере четыре точки, не лежащие в одной плоскости. Следствия из аксиом I группы:

1.Две различные прямые имеют не более чем одну общую точку.

2.Если две различные плоскости имеют одну общую точку, то они имеют общую прямую, которой принадлежат все общие точки данных плоскостей.

3.Плоскость и не принадлежащая ей прямая имеют не более чем одну общую точку.

4.Прямая и не принадлежащая ей точка определяют одну и только одну плоскость.

5.Каждой плоскости принадлежит по крайней мере три точки, не принадлежащие одной прямой.

12

Пользуясь аксиомами только первой группы, нельзя доказать, например, что на прямой существуют более, чем две точки или что на плоскости существуют более, чем три точки.

II. Аксиомы порядка

Обозначение: если точка В лежит между точками А и С, то это может быть записано: (АВС) или А–В–С.

II1. Если А–В–С, то А, В, С – различные точки одной прямой и С–В–А.

II2. Каковы бы ни были две точки А и В, существует по крайней мере одна точка С на прямой АВ такая, что А–В–С.

II3. Среди любых трех точек прямой существует не более одной точки, лежащей между двумя другими.

Опред. Пару точек А и В называют отрезком и обозначают АВ или ВА. Точки, ле-

жащие между А и В, называются внутренними точками или точками отрезка АВ. Ос-

тальные точки прямой АВ называются внешними к отрезку АВ.

Замечание. В аксиомах II1–II3 не утверждается, что между точками А и В существуют другие точки, т.е. из них не видно, что каждый отрезок имеет внутренние точки. Но из II2 следует, что каждый отрезок имеет внешние точки.

II4. (аксиома Паша). Пусть А, В, С – три точки, не лежащие на одной прямой, а а – прямая в плоскости АВС, не проходящая ни через одну из точек А, В, С. Тогда, если прямая а проходит через точку отрезка AB, то она проходит через точку отрезка АС или ВС.

Аксиомы I и II групп позволяют ввести понятия полуплоскости, луча и полупространства.

Следствия из аксиом I и II групп

1.Прямая а, лежащая в плоскости П, разделяет множество точек этой плоскости, не лежащих на прямой а, на два непустых подмножества так, что если точки А и В принадлежат одному подмножеству, то отрезок АВ не имеет общих точек с прямой а; если же эти точки принадлежат разным подмножествам, то отрезок АВ имеет общую точку с прямой а.

Замечание. Каждое из подмножеств, определяемых следствием 1, называется полуплоскостью плоскости П с границей а. Аналогично вводится понятие луча и полупространства.

Угол – пара лучей h и k, исходящих из точки О и не лежащих на одной прямой.

2.Каковы бы ни были точки А и С, существует по крайней мере одна точка D на прямой АС, лежащая между А и С.

3.Среди любых точек А, В, С одной прямой всегда существует одна, лежащая между двумя другими.

4.Если точки А, В, С не лежат на одной прямой и если некоторая прямая а пересекает какие-либо два из трех отрезков АВ, ВС, АС, то она не пересекает третий из этих отрезков.

5.Если В лежит на отрезке АС и С – на отрезке BD, то В и С лежат на отрезке AD. Если С лежит на отрезке AD и В – на отрезке АС, то В лежит на отрезке AD и С – на отрезке BD.

6.Между любыми двумя точками прямой существует бесконечное множество других её точек.

13

7.Если точки С и D лежат между точками А и В, то все точки отрезка CD принадлежат отрезку АВ.

Замечание. В этом случае говорят, что отрезок CD лежит внутри отрезка АВ.

8.Если А–С–В, то все точки отрезка АС принадлежат отрезку АВ. Если А–С–В, то никакая точка отрезка АС не может быть точкой отрезка СВ. Если А–С–В, то каждая точка отрезка АВ, отличная от С, принадлежит либо отрезку АС, либо отрезку СВ.

III. Аксиомы конгруэнтности

Предполагается, что отрезок (угол) находится в известном отношении в какому-то отрезку (углу). Это отношение выражается словом "конгруэнтны" или "равен" и обозначается символом "=". Отношение конгруэнтности должно удовлетворять требованиям следующих аксиом.

III1. Если даны отрезок АВ и луч, исходящий из точки А', то существует точка В', принадлежащая данному лучу, такая, что АВ = А'В'.

III2. Если A'B' = АВ и A''B'' = АВ, то A'B' = A''B''.

Следствие. Каждый отрезок конгруэнтен самому себе

III3. Пусть А–В–С, A'–B'–C', АВ = A'B', ВС = B'C'. Тогда АС = A'C'.

III4. Пусть даны (h, k) на плоскости П, прямая a' на этой же плоскости или какойнибудь другой плоскости П', и задана определенная сторона плоскости П' относительно прямой а'. Пусть h' – луч прямой а', исходящий из точки O'. Тогда на плоскости П' существует один и только один луч k' такой, что (h, k) конгруэнтен (h', k') и при этом все внутренние точки (h', k') лежат по заданную сторону от а'.

Следствие. Каждый угол конгруэнтен самому себе Замечание. Первая часть аксиомы может быть выражена так: каждый угол может

быть однозначно отложен в данной плоскости по данную сторону при данном луче.

III5. Пусть А, В, С – три точки, не лежащие на одной прямой, и A', B', C' – три точки, не лежащие на одной прямой. Если при этом AB = A'B', AC = A'C', BAC = B'A'C', то

АВС = A'B'C'.

Следствия из аксиом I – III

1.В равнобедренном треугольнике углы при основании равны.

2.Пусть даны три точки А, В, С на прямой а и три точки A', B', C' на прямой а'. Пусть, далее, АВ = A'B' и АС = A'C'. Тогда если А–В–С, а B' на прямой а' лежит с той же стороны от точки A', что и С', то A'–B'–C'.

Опред. Треугольник АВС называется конгруэнтным треугольнику A'B'C', если

АВ = A'B', АС = A'C', ВС = B'C', А = A', B = B', C = C'. 3. Признаки равенства треугольников

Опред. Два угла, у которых имеются общая вершина и одна общая сторона, а другие стороны которых составляют прямую линию, называются смежными углами. Два угла с общей вершиной, стороны которых попарно составляют прямые линии, называются вертикальными углами. Угол, конгруэнтный своему смежному, называется прямым.

4.Если два угла взаимно конгруэнтны, то смежные с ними углы также взаимно конгруэнтны.

5.Вертикальные углы конгруэнтны между собой.

6.Прямые углы существуют.

7.Все прямые углы конгруэнтны между собой.

8.Для каждого отрезка существует единственная середина; середина отрезка является его внутренней точкой.

14

9.В равнобедренном треугольнике медиана основания есть в то же время высота и биссектриса угла при вершине.

10.Каждый угол можно разделить пополам и притом единственным образом.

11.Из любой точки можно опустить на данную прямую один и только один перпендикуляр.

12.Из каждой точки на прямой можно восстановить к этой прямой единственный перпендикуляр.

Опред. Если даны два отрезка АВ и A'B' и внутри АВ существует такая точка С, что АС = A'B', то говорят, что отрезок АВ больше отрезка A'B' (АВ > A'B') или отрезок A'B' меньше отрезка АВ (A'B' < АВ).

13.Для произвольных отрезков АВ и CD всегда выполняется одно из трех соотношений: АВ = CD, АВ > CD, AB < CD, причем каждое из них исключает два других.

14.Если AB < A'B' и A'B' < A''B'', то AB < A''B''.

15.Внешний угол треугольника больше каждого внутреннего, не смежного с ним.

16.Во всяком треугольнике по крайней мере два угла острые.

17.В треугольнике бОльшая сторона лежит против бОльшего угла, и обратно, бОльший угол лежит против бОльшей стороны.

18.Перпендикуляр короче наклонной.

19.Каждая сторона треугольника меньше суммы и больше разности двух других его

сторон.

Аксиомы третьей группы позволяют определить движение.

IV. Аксиомы непрерывности

IV1. (Аксиома Архимеда) Пусть АВ и CD – произвольные отрезки. Тогда на прямой АВ существует конечное число точек А1, А2, ..., Аn, расположенных так, что А–А1–А2–...

–Аn–В, причем отрезки АА1, А1А2, ..., Аn–1An конгруэнтны отрезку CD и А–В–Аn

	A		В
	A1	A2	An–1 An
С	D

IV2. Пусть на произвольной прямой а дана бесконечная последовательность отрезков А1В1, А2В2, ..., из которых каждый последующий лежит внутри предыдущего и, кроме того, для любого отрезка CD найдется натуральное число n, такое, что АnBn меньше CD. Тогда на прямой а существует точка Х, лежащая внутри каждого из отрезков А1В1,

А2В2, ....

А1 А2 А3 Х В3 В2 В1

Замечание. Из условия аксиомы следует, что точка Х – единственная, так как если существует еще другая точка Y, лежащая внутри всех этих отрезков, то при любом n отрезок АnBn будет больше отрезка ХY, что противоречит аксиоме.

Аксиомы IV группы (при сохранении аксиом I-III) эквиваленты предложению Деде-

кинда:

Пусть дано разбиение точек отрезка [AB] на два класса К1 и К2 (К1 К2 = [AB], К1 К2 = ), удовлетворяющее двум условиям:

1) А К1, В К2 и классы К1 и К2 содержат точки, отличные от точек А и В.

15

2) любая точка класса К1, отличная от А, лежит между точкой А и любой точкой класса К2.

Тогда существует точка М0 отрезка [AB], такая, что любая точка, лежащая между А и М0 принадлежит классу К1, а любая точка между М0 и В – классу К2. Разбиение отрезка [AB] на классы К1 и К2, удовлетворяющее условиям 1-2, называ-

ют дедекиндовым сечением. О точке М0 говорят, что она производит это сечение. Легко доказать, что такая точка единственная, она может принадлежать как первому, так и второму классу.

К важнейшим следствиям из аксиом I–IV относится теория измерения отрезков и углов, о порядке расположения точек на прямой, а также теоремы о пересечении прямой и окружности и двух окружностей.

V. Аксиома параллельности

V. Пусть а – произвольная прямая и А – точка, лежащая вне прямой а; тогда в плоскости, определенной точкой А и прямой а, можно провести не более одной прямой, проходящей через точку А и не пересекающей а.

На основе аксиом I-V можно построить теорию параллельных прямых по Евклиду, доказать теоремы о сумме углов треугольника и выпуклого многоугольника, изучить свойства параллелограммов и трапеций, построить теорию подобия и т.д., обосновать обычную тригонометрию и декартову аналитическую геометрию. Можно также ввести понятия площади многоугольника и объема многогранника.

3.1.3. Некоторые следствия из аксиом аксиоматики Гильберта

Следствия из I

Следствие I.1. 1) Две прямые имеют не более одной общей точки; 2) две различные плоскости либо не имеют совсем общих точек, либо имеют общую прямую, на которой лежат все общие точки этих двух плоскостей; 3) плоскость и не лежащая на ней прямая имеют не более одной общей точки

Доказательство

1)Согласно I1 и I2

2)Пусть две плоскости и имеют общую точку А. I7 => В и => по I1 АВ => I6 AB состоит из общих точек и . При этом АВ содержит ВСЕ общие точки и . Допустим, что это не так, и у плоскостей и есть общая точка С АВ => I5 = , что противоречит условию.

3)следует из I6.

Следствие I.2. Через прямую и не лежащую на ней точку, так же как через две прямые с общей точкой, проходит одна и только одна плоскость.

Доказательство Пусть даны прямая а и точка А а.

I3: В, С а

I2: А, В, С не лежат на одной прямой

I4,5: ! : А, В, С . I6: а .

Следствие I.3. Каждая плоскость содержит по крайней мере три точки. Доказательство

16

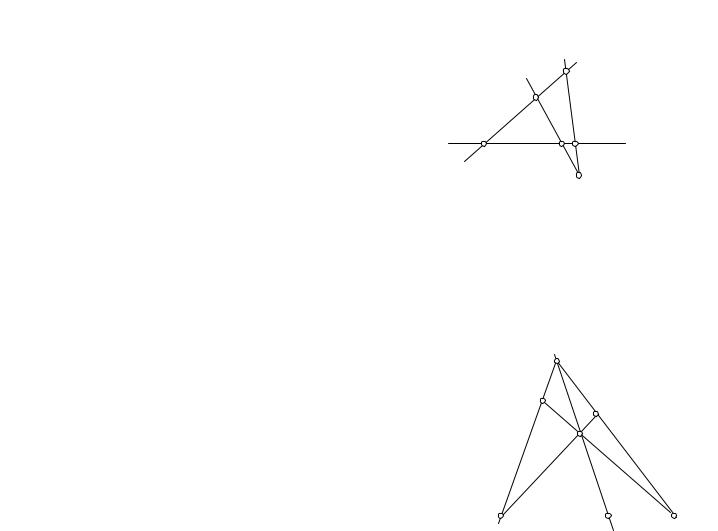
Пусть дана плоскость

I4: А

I8: B

I3: C AB

Плоскости АВС и имеют общую точку А => I7: D ABC и => доказано существование двух точек, лежащих на данной плоскости.

I8: E ABD

I4: ABE ABD

I7: ABE и имеют общую точку F, причем по I6: F АВ.

Так как D и F АВ, то по следствию 1 эти точки не могут быть общими точками плоскостей ABD и ABF => D и F – различны.

Доказано, что в существует три точки A, D и F.

	Следствия из II
	Следствие II.1. Каковы бы ни были точки А и С, существует по крайней мере одна
точка D на прямой АС: А–D–С.
	Доказательство			F
	1)	I3: Е АС, II2: F AE: A-E-F.		E
	2)	II2: G F-C-G => (F-G-C), т.е. G [FC]	A	C
	3)	II4: EG должна пересечь [AC] или [FC].
				D
	Но EG не может пересечь [FC], иначе по
				G
I1	и I2 все рассмотренные точки лежали бы
на одной прямой, что противоречит 1)
Т.о. EG АС = D => A-D-C

Следствие II.2. Среди любых точек А, В, С одной прямой всегда существует одна,

лежащая между двумя другими
Доказательство
Пусть (В-А-С) и (А-С-В).
I3: D AC => DB		G
II2: G BD: B-D-G	F
I4: для BCG и AD – AD CG = E: C-E-G			E
Аналогично для АВG и CD: AG CF = F		D
и A-F-G
AEG и CF: AE CF = D, A-D-E
AEC и BD: A-B-C, так как (E-G-C)
Замечание. Как следствие из Сл.II.2 может быть	А	B	C

доказано следующее утверждение:

Если точки А, В, С не лежат на одной прямой и если некоторая прямая а пересекает какие-либо два из трех отрезков АВ, ВС и АС, то она не пересекает третий из этих отрезков.

Аксиомы II.2 в соединении теоремой 4 и аксиома II.З в соединении со следствием II.2 позволяют формулировать следующие две теоремы:

17

А) Каковы бы ни были две точки А и С, существуют точки, лежащие внутри отрезка АС, и точки, лежащие на прямой АС вне этого отрезка.

Б) Из трех точек прямой всегда одна и только одна лежит между двумя другими.

Самостоятельно разобрать доказательства:

–дополнение аксиомы Паша

–Лемма 1. Если В лежит на отрезке АС и С — на отрезке BD, то В и С лежат на отрезке AD.

Доказательство. Основываясь на аксиомах I.3 и II.2, выберем точку Е, не лежащую на прямой АВ, а на прямой ЕС – такую точку F, что Е лежит между С и F (рис.). Так как

Влежит на отрезке АС, то, применяя к треугольнику АЕС и прямой FB аксиому II.4, заключаем, что прямая FB должна пересечь либо отрезок АЕ, либо отрезок ЕС. Так как точка Е лежит между F и С, то по аксиоме II.З точка F не может лежать между Е и С. Следовательно, прямая FB должна пересечь отрезок АЕ. Применяя аксиому II.4 к треугольнику FBC и прямой АЕ и снова используя аксиому II.З, найдем, что точка пересечения отрезка АЕ и прямой FB лежит между точками F и В. Обозначим эту точку пересечения буквой G. Аналогично доказывается (путем применения аксиомы II.4 к треугольнику GBD и к прямой CF с последующим использованием аксиомы II.З), что прямая CF встречает отрезок GD в некоторой точке Н. Так как при этом Н лежит на отрезке GD, a Е, по аксиоме II.З, не принадлежит отрезку AG, то согласно аксиоме II.4 прямая ЕН имеет общую точку с отрезком AD, т. е. С лежит на отрезке AD. Совершенно аналогично можно доказать, что и В принадлежит этому отрезку.

Лемма 2. Если С лежит на отрезке AD и В – на отрезке АС, то В лежит также на отрезке AD u С – на отрезке BD.

Доказательство. Выберем вне прямой АВ точку G и потом выберем точку F так, чтобы G находилась на отрезке BF (рис.).

Вследствие аксиом I.2 и II.З прямая CF не имеет общих точек ни с отрезком АВ, ни с отрезком BG, а тогда, согласно аксиоме II.4, она не имеет общих точек также и с отрезком AG. Но так как С лежит на отрезке AD, то согласно аксиоме II.4 применительно к треугольнику AGD прямая CF должна встретить отрезок GD в некоторой точке Н.

Отсюда и снова из аксиомы II.4 применительно к треугольнику BGD следует, что прямая FH пересекает отрезок BD. Таким образом, С лежит на отрезке BD.

Первое утверждение леммы 2 вытекает тогда из леммы 1.

– Теорема о существовании бесконечного множества точек на отрезке (Т6) Следствие II.3. Между любыми двумя точками прямой существует бесконечное

множество других ее точек.

18

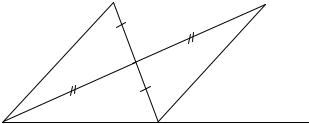
Доказательство. Пусть А, В – две точки прямой а. Согласно следствию II.1 между А и В существует точка С; по той же теореме, между А и С существует точка D. В силу леммы 2 точка D лежит также между А и В и, следовательно, А, В, С, D – различные точки прямой а. Аналогично можно утверждать, что между А и D лежит точка Е и что эта точка лежит также между А и С и между А и В, следовательно, точки А, В, С, D, Е различны. Повторяя то же рассуждение, установим, что между А и В находится бесконечное множество точек С, D, Е, ..., и тем самым докажем теорему.

–Теорема о точках отрезка CD, лежащего на отрезке AB (Т7).

–Теорема о точке, лежащей между двумя другими (Т8а,б)

–Теорема о разбиении прямой на два подмножества (Т9)

–Теорема о разбиении плоскости прямой на два подмножества (Т10)

Следствия из III

Следствие III.1. (первый признак равенства треугольников) Если для двух треугольников АВС и A'B'C' имеет место: AB = A'B', AC = A'C', A = A', то треугольник АВС конгруэнтен треугольнику A'B'C'.

Доказательство

III5: B = B', C = C'. Необходимо доказать, что BC = B'C'.

Допустим, это не так. По III1: D' B'C': BC = B'D'. При нашем допущении лучи А'C' и A'D' – разные. По III5 для АВС A'B'C' – ВАС = B'A'D'. Но по условиюBAC = B'A'C' => противоречие требованию единственности в аксиоме III4. Наше предположение не верно и BC = B'C'.

Теорема. Внешний угол произвольного треугольника больше каждого внутреннего угла, не смежного с ним.

В школьных учебниказ эта теорема является следствием теоремы о сумме углов треугольника и, значит, использует аксиому параллельных. В действительности она может быть доказана без использования этой аксиомы.

В F

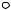Е

А

С

D

А именно, пусть АВС – произвольный треугольник. Рассмотрим, например, внешний угол ВСD, и докажем, что он больше внутреннего угла АВС. Для этого через вершину А и середину Е стороны ВС проведем прямую и отложим на ней отрезок EF, равный АЕ. Треугольники АВЕ и FCЕ равны по первому признаку равенства треугольников (ВЕ = ЕС, AE = FE, AEB = FEC). Следовательно, ABC = BCF. Но, так как точка F лежит внутри угла BCD, то угол BCF составляет только часть угла BCD.

Значит, BCD > ABC.

Следствие 1. Если в треугольнике имеется прямой или тупой угол, то остальные два угла этого треугольника – острые.

19

Действительно, в этом случае внешний угол, например, к тупому углу будет острым и он больше каждого внутреннего угла, не смежного с ним.

Следствие 2. Через точку, не принадлежащую прямой, проходит не более одной прямой, перпендикулярной данной.

Действительно, если бы имелось две прямые, перпендикулярные данной, то они образовывали бы треугольник с двумя прямыми углами, что невозможно (внешний угол был бы равен внутреннему, не смежному с ним)

20