
В чем заключается этап агрегирования? Стр 43
Агрегирование (Aggregation). Агрегирование представляет собой процедуру определения степени истинности условии по каждому из правил системы нечеткого вывода.
Формально
процедура агрегирования выполняется
следующим образом. До начала этого этапа
предполагаются известными значения
истинности всех под условием системы
нечеткого вывода, т. е. множество значений
 .
Далее рассматривается каждое из условий
правил системы нечеткого вывода. Если
условие правила представляет собой
нечеткое высказывание вида 1 или 2, то
степень его истинности равна
соответствующему значению
.
Далее рассматривается каждое из условий
правил системы нечеткого вывода. Если
условие правила представляет собой
нечеткое высказывание вида 1 или 2, то
степень его истинности равна
соответствующему значению .
.
Если
же условие состоит из нескольких
подусловий вида (1.10), причем лингвистические
переменные в подусловиях попарно не
равны друг другу, то определяется степень
истинности сложного высказывания на
основе известных значений истинности
подусловий. При этом для определения
результата нечеткой конъюнкции или
связки «И» может быть использована
формула пересечения нечетких множеств,
а для определения результата нечеткой
дизъюнкции или связки «ИЛИ» может быть
использована формул объединения нечетких
множеств. При этом значения
 используются в качестве аргументов
соответствующих логических операций.
Тем самым находятся количественные
значения истинности всех условий правил
системы нечеткого вывода.
используются в качестве аргументов
соответствующих логических операций.
Тем самым находятся количественные
значения истинности всех условий правил
системы нечеткого вывода.
Этап
агрегирования считается законченным,
когда будут найдены все значения
 для
каждого из правил
для
каждого из правил
 ,
входящих в рассматриваемую базу правил
,
входящих в рассматриваемую базу правил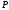 системы
нечеткого вывода. Это множество значений
обозначим
через
системы
нечеткого вывода. Это множество значений
обозначим
через
 .
.
Пример
1.10.
Для иллюстрации выполнения этого этапа
рассмотрим пример процесса агрегирования
двух нечетких высказываний: “скорость
автомобиля
средняя”
И “кофе
горячий”
и “скорость
автомобиля средняя”
ИЛИ “кофе
горячий”
для входной лингвистической переменной
 - скорость движения автомобиля и
- скорость движения автомобиля и
 -
температура кофе. Предположим, что
текущая скорость автомобиля равна 55
км/ч, т. е.
-
температура кофе. Предположим, что
текущая скорость автомобиля равна 55
км/ч, т. е. =55
км/ч, а температура кофе равна
=55
км/ч, а температура кофе равна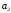 =70ْ
С.
=70ْ
С.
Тогда
агрегирование первого нечеткого
высказывания с использованием операции
нечеткого конъюнкции дает в результате
число
 (приближенное
значение), которое означает его степень
истинности и получается как минимальное
из значений 0.67 и 0.8 (рисунок 1.10а).
Агрегирование второго нечеткого
высказывания с использованием операции
нечеткой дизъюнкции дает в результате
число
(приближенное
значение), которое означает его степень
истинности и получается как минимальное
из значений 0.67 и 0.8 (рисунок 1.10а).
Агрегирование второго нечеткого
высказывания с использованием операции
нечеткой дизъюнкции дает в результате
число
 ,
которое означает его степень истинности
и получается как максимальное из значений
0.67 и 0.8 (рисунок 1.10б).
,
которое означает его степень истинности
и получается как максимальное из значений
0.67 и 0.8 (рисунок 1.10б).

Рис. 1.10. Примеры агрегирования подусловий для нечеткого высказывания
“скорость автомобиля средняя” И “температура кофе высокая” (а)

Рис. 1.10. Примеры агрегирования подусловий для нечеткого высказывания
“скорость автомобиля средняя” ИЛИ “температура кофе высокая” (б)
В чем особенности нейрона с сигмоидой на выходе
Модель нейрона с сигмоидой на выходе
Структура нейрона с сигмоидой на выходе аналогична структурам ранее обсуждавшихся моделей, т.е. персептрона и нейрона типа Адалайн (см. рисунок 2.10).

Рис. 2.10. График униполярной функции активации
при различных значениях параметра β
Название обусловлено функцией активации, которая имеет форму сигмоидальной униполярной или биполярной функции. Это непрерывные функции, описывающиеся выражениями:
- униполярная функция

- биполярная функция

На рисунке 2.10 представлены графики униполярных функций при различных значениях параметра бетта. Читатель может заметить, что при малых значениях параметра бетта функция имеет плавный характер, но с ростом значения этого параметра график становится более крутым вплоть до обретения порогового вида. Огромным достоинством сигмоидальных нейронов считается дифференцируемость функции активации. Кроме того, производные этих функций легко вычисляются, поскольку они приобретают следующие формы:
- для униполярной функции:
 (2.56)
(2.56)
- для биполярной функции:
 (2.57)
(2.57)
Структура нейрона с сигмоидой на выходе представлена на рис. 6.11. Выходной сигнал описывается выражением
 (2.58)
(2.58)

Рис. 2.11. Структура нейрона с сигмоидой на выходе
Мера погрешности Q определяется как квадрат разности между эталонным значением и значением, полученным на выходе нейрона, т.е.:
 (2.59)
(2.59)
Так же, как и в ситуации с нейроном типа Адалайн, для обучения используется правило наискорейшего спуска, однако теперь должна учитываться функция активации. Веса нейрона модифицируются согласно выражению
 (2.60)
(2.60)
Рассчитаем производную меру погрешности относительно весов. Очевидно, что
 (2.61)
(2.61)
 (2.62)
(2.62)
Следовательно
 (2.63)
(2.63)
Легко заметить, что
 .
(2.64)
.
(2.64)
Введем обозначение
 .
(2.65)
.
(2.65)
Согласно формулам (2.60) и (2.65), веса на шаге (t+1) модифицируются следующим образом:
wi(t +1)= wi(t)-ηδxi = wi(t) + η(d - f(s)) f'(s)xi. (2.66)
Теперь рассмотрим альтернативный способ обучения сигмоидального нейрона с применением алгоритма RLS. Рассмотрим два случая, различающиеся способом определения погрешности. В первом случае сигнал погрешности определяется на выходе линейной части нейрона. Поэтому мера погрешности имеет вид
 (2.67)
(2.67)
где
для
униполярной функции,
для
биполярной функции. (2.68)
(2.68)
В этой ситуации погрешность интерпретируется как заданный сигнал на выходе линейной части нейрона. Нормальное уравнение принимает вид
 ,
(2.69)
,
(2.69)
либо в векторной форме
r(t) = R(t) w(t), (2.70)
где
 (2.71)
(2.71)
 (2.72)
(2.72)
Обратим внимание, что уравнения (2.71) и (2.72) аналогичны уравнениям (2.34) и (2.35). Поэтому алгоритм RLS принимает форму
e(t)=b(t)-xT(t)w(t-1)=b(t)-s(t); (2.73)
 (2.74)
(2.74)
P(t)=λ-1[I-g(t)xT(t)]P(t-1); (2.75)
w(t) = w(t-1) + g(t)e(t), ( 2.76)
причем начальные условия определяются выражением (2.55).
Во втором случае погрешность определяется на выходе нелинейной части нейрона. Мера погрешности имеет вид
 (2.76)
(2.76)
В результате дифференцирования меры (2.77) относительно вектора w(t) и приравнивания полученного выражения к нулю получаем
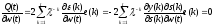 (2.78)
(2.78)
Дальнейшие вычисления дают:
 (2.79)
(2.79)
В результате применения подстановки Тейлора к содержимому квадратных скобок формулы (2.79) получаем
f(b(k)) ≈ f(S(k))+f'(s(k)))b(k)-s(k)), (2.80)
где
b(t) = f-1(d(t)). (2.81)
В итоге выражения (6.79) и (6.80) сводятся к уравнению
 .
(2.82)
.
(2.82)
Уравнение (2.82) в векторной форме имеет вид
r(t) = R(t)w(t), (2.83)
где
 (2.84)
(2.84)
 (2.85)
(2.85)
При использовании в выражениях (2.73), (2.76) подстановок
х(k)→ f'(s(k))x(k); (2.86)
b(k) → f'(s(k))b(k) (2.87)
получаем форму алгоритма RLS, адаптированную к обучению сигмоидального нейрона:
 ;
(2.88)
;
(2.88)
 (2.89)
(2.89)
 (2.90)
(2.90)
 (2.91)
(2.91)
Начальные условия определяются в соответствии с формулой (2.55).
В чем отличие алгоритма Мамдани от других нечетких алгоритмов?
Чем отличается алгоритм Мамдани от алгоритма Сугено?
Какие алгоритмы нечеткого вывода Вы знаете? Стр 57
Алгоритм Мамдани (Mamdani). Алгоритм Мамдани является одним из первых, который нашел применение в системах нечеткого вывода. Он был предложен в 1975 г. Английским математиком Е. Мамдани (Ebrahim Mamdani) в качестве метода для управления паровым двигателем. По своей сути этот алгоритм порождает рассмотренные выше этапы, поскольку в наибольшей степени соответствует их параметрам.
Формально алгоритм Мамдани может быть определен следующим образом.
- Формирование базы правил систем нечеткого вывода. Особенности формирования базы правил совпадают с рассмотренными выше при описании данного этапа.
- Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.
- Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий каждого из правил нечетких продукций используются парные нечеткие логические операции. Те правила, степень истинности условий которых отлична от нуля, считаются активными и используются для дальнейших расчетов.
- Активизация подзаключений в нечетких правилах продукций. Осуществляется по формуле (6.4), при этом для сокращения времени вывода учитываются только активные правила нечетких продукций.
- Аккумуляция заключений нечетких правил продукций осуществляется по формуле объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.
- Дефаззификация выходных переменных. Традиционно используется метод центра тяжести в форме (1.16).
Алгоритм Цукамото (Tsukamoto). Формально алгоритм Цукамото может быть определен следующим образом.
- Формирование базы правил систем нечеткого вывода. Особенности формирования базы правил совпадают с рассмотренными выше при описании данного этапа.
- Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.
-
Активизация подзаключений в нечетких
правилах продукций. Осуществляется
использованием формулы (1.12), посредством
чего находится совокупность нечетких
множеств:
 ,
где q—
общее количество подзаключений в базе
правил.
,
где q—
общее количество подзаключений в базе
правил.
- Аккумуляция заключений нечетких правил продукций. Осуществляется по формуле объединения нечетких множеств, соответствующих термам подзаключений, относящихся к одним и тем же выходным лингвистическим переменным.
- Дефаззификация выходных переменных. Может использоваться любой из рассмотренных выше методов дефаззификации.
Алгоритм Сугено (Sugeno). Формально алгоритм Сугено, предложенный Сугено и Такаги, может быть определен следующим образом.
- Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукции в форме:
ПРАВИЛО<#>:ЕСЛИ“![]() есть
есть![]() ”И“
”И“![]() есть
есть![]() ”ТО“
”ТО“ ”.
(1.20)
”.
(1.20)
Здесь
 - некоторые весовые коэффициенты. При
этом значение выходной переменной w
в
заключении определяется как некоторое
действительное число.
- некоторые весовые коэффициенты. При
этом значение выходной переменной w
в
заключении определяется как некоторое
действительное число.
- Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.
- Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min – конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считается активными и используются для дальнейших расчетов.
-
Активизация подзаключений в нечетких
правилах продукций. Во-первых, с
использованием метода (1.12) находятся
значения степени истинности всех
заключений правил нечетких продукций.
Во-вторых, осуществляется расчет обычных
(не нечетких) значений выходных переменных
каждого правила. Это выполняется с
использованием формулы для заключения
(1.20), в которую вместо
 и
и
 подставляются значения входных переменных
до этап фаззификации. Тем самым
определяются множество значений
подставляются значения входных переменных
до этап фаззификации. Тем самым
определяются множество значений и множество значений выходных переменных
и множество значений выходных переменных![]() ,
где n— общее количество правил в базе
правил.
,
где n— общее количество правил в базе
правил.
-
Аккумуляция заключений нечетких правил
продукций. Фактически отсутствует,
поскольку расчеты осуществляются с
обычными действительными числами
 .
.
- Дефаззификация выходных переменных. Используется модифици-рованный вариант в форме метода центра тяжести для одноточечных множеств.
Упрощенный алгоритм нечеткого вывода. Формально упрощенный алгоритм может быть определен следующим образом.
Формирование базы правил систем нечеткого вывода. В базе правил используются только правила нечетких продукции в форме:
ПРАВИЛО
<#>: ЕСЛИ “![]() есть
есть
 ”
И “
”
И “![]() есть
есть
![]() ”
ТО “
”
ТО “ ”.
(1.21)
”.
(1.21)
Здесь
 - некоторое действительное число.
- некоторое действительное число.
Фаззификация входных переменных. Особенности фаззификации совпадают с рассмотренными выше при описании данного этапа.
- Агрегирование подусловий в нечетких правилах продукций. Для нахождения степени истинности условий всех правил нечетких продукций, как правило, используется логическая операция min – конъюнкции. Те правила, степень истинности условий которых отлична от нуля, считается активными и используются для дальнейших расчетов.
-
Активизация подзаключений в нечетких
правилах продукций. Осуществляется с
использованием метода (1.13), посредством
чего находятся значения степеней
истинности всех заключений правил
нечетких продукций
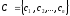 где n— общее количество правил в базе
правил.
где n— общее количество правил в базе
правил.
-
Аккумуляция заключений нечетких правил
продукций. Фактически отсутствует,
поскольку расчеты осуществляются с
обычными действительными числами
 .
.
- Дефаззификация выходных переменных. Используется модифицированный вариант в форме метода центра тяжести для одноточечных множеств.
При решении практических задач нечетких задач нечеткого моделирования могут одновременно использоваться несколько алгоритмов нечеткого вывода с целью получения наиболее адекватных результатов. Ниже рассматриваются примеры применения некоторых из этих алгоритмов в задачах нечеткого управления.
В чем отличие модели персептрона от общей модели нейрона?
Что включает в себя модель искусственного нейрона?
Нейрон и его модель (персептрон)
8.1 Структуру и функционирование одиночного нейрона
Базовый элемент нервной системы - нервная клетка, называемая нейроном. На рисунке 2.1 представлена упрощенная модель нейрона. В нейроне можно выделить тело клетки, называемое сомой, а также исходящие из него два вида отростков: а) по которым в нейрон поступает информация - дендриты и б) по которым нейрон передает информацию - аксон. Каждый нейрон имеет только один выходной отросток, по которому он может передавать импульс другим нейронам.

Рис. 2.1. Упрощенная модель нейрона и его соединения с соседним нейроном
1 - тело клетки; 2 - аксон; 3 - дендриты; 4 - синапсы
Одиночный нейрон принимает возбуждения от огромного количества нейронов (их число может достигать тысячи). Как уже отмечалось, мозг человека состоит из порядка 1011 нейронов, которые взаимодействуют через огромное количество соединений. Каждый нейрон передает возбуждение другим нейронам через нервные стыки, называемые синапсами, при этом процесс передачи сигналов имеет сложную электрохимическую природу. Синапсы играют роль репитеров информации, в результате функционирования которых возбуждение может усиливаться или ослабляться. Как следствие, к нейрону приходят сигналы, одна часть из которых оказывает возбуждающее, а вторая - тормозящее воздействие. Нейрон суммирует возбуждающие и тормозящие импульсы. Если их алгебраическая сумма превышает некоторое пороговое значение, то сигнал с выхода нейрона пересылается посредством аксона к другим нейронам.
Рассмотрим модель нейрона, связанную с первыми попытками формализовать описание функционирования нервной клетки. Введем следующие обозначения: п - количество входов нейрона; х1,...,хn - входные сигналы, х = [х1,…, хn]T; w0,…,wn - синаптические веса, w =[w0,..., wn]T; у - выходной сигнал нейрона; w0 - пороговое значение; f- функция активации.
Формула, описывающая функционирование нейрона, имеет вид
y = f(s), (2.1)
где

Выражения (2.1) и (2.2) описывают нейрон, представленный на рисунке 2.2.

Рис. 2.2. Модель нейрона
Функция активации f может принимать различные формы в зависимости от конкретной модели нейрона.
Как следует из приведенных формул, нейрон функционирует очень простым образом. Вначале входные сигналых0, хи ...,хп умножаются на соответствующие им веса w0, wx, ..., wn. Полученные значения суммируются. В результате возникает сигнал s, отражающий функционирование линейной части нейрона. Этот сигнал подается на вход функции активации, которая чаще всего имеет нелинейный характер. Предположим, что значение сигнала
х0 равно 1, а вес w0 называется порогом (англ. bias). Где хранятся знания в нейроне, имеющем такое описание? Оказывается, что знания хранятся именно в весах. Однако наибольшим феноменом оказывается то, что нейроны очень легко обучаются (при помощи алгоритмов, описываемых в следующих разделах текущей главы), причем обучение сводится к подбору значений весов.
На рисунке 2.2 изображена обобщенная модель нейрона, однако в искусственных нейронных сетях применяются его конкретные модификации. Некоторые частные модели нейрона будут обсуждаться в следующих разделах. Необходимо отметить, что искусственные нервные клетки, структура которых соответствует рисунке 2.2, соединяются между собой в математических моделях также как и их оригиналы в настоящем мозге. Способы соединения нейронов, а также методы обучения возникающих при этом структур мы также будем рассматривать в следующих разделах.
