
- •Определение дифференциального уравнения. Основные понятия.
- •Дифференциальные уравнения первого порядка.Теорема существования и единственности решения.
- •Дифференциальные уравнения первого порядка с разделяющимися переменными.
- •Линейные дифференциальные уравнения первого порядка.
- •Определение дифференциальных уравнений второго порядка. Основные понятия.
- •Линейные дифференциальные уравнения второго порядка. Фундаментальная система решений (фср). Теоремы об общем решении.
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами их частные решения в зависимости от вида правой части. Метод вариации произвольных постоянных.
- •Определение степенного ряда. Теорема Абеля. Радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов.
- •Численное решение обыкновенных дифференциальных уравнений
Линейные дифференциальные уравнения первого порядка.
Определение.
Дифференциальное уравнение вида
 ,
где
,
где
 ,
,
 ,
, - известные функции, называется линейным
дифференциальным уравнением первого
порядка.
- известные функции, называется линейным
дифференциальным уравнением первого
порядка.
Это уравнение
делением на
 можно привести к виду
можно привести к виду
 ,
(3)
,
(3)
где
 .
Это уравнение линейно, так какy
и
.
Это уравнение линейно, так какy
и
 в первой степени. Если
в первой степени. Если ,
то линейное уравнение называется
однородным.
,
то линейное уравнение называется
однородным.
Способами решения уравнения (3) являются: метод Бернулли и метод Лагранжа (метод вариации произвольной постоянной).
Умножим обе части
уравнения (3) на
 .
Получим
.
Получим .
Найдем производную функции
.
Найдем производную функции ,
то есть
,
то есть =
= .
.
Определение дифференциальных уравнений второго порядка. Основные понятия.
Определение.
Дифференциальным уравнением второго
порядка называется уравнение вид (5) или
(5) или
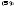 .
.
Определение.
Общим решением дифференциального
уравнения (5) называется функция вида
 ,
зависящая от двух произвольных постоянных
,
зависящая от двух произвольных постоянных и
и и удовлетворяющая уравнению (5) при
любых значениях
и удовлетворяющая уравнению (5) при
любых значениях и
и .
.
Определение.
Частным решением дифференциального
уравнения (5) называется функция
 ,
полученная из общего решения при
конкретных значениях постоянных
,
полученная из общего решения при
конкретных значениях постоянных .
.
Начальные условия
для дифференциального уравнения второго
порядка задаются с помощью трех чисел
 или
или и
и .
Иначе говоря, задается точка
.
Иначе говоря, задается точка и угловой коэффициент касательной
и угловой коэффициент касательной к интегральной кривой в данной точке.
Частное решение дифференциального
уравнения, удовлетворяющее заданным
начальным условиям, называется решением
задачи Коши.
к интегральной кривой в данной точке.
Частное решение дифференциального
уравнения, удовлетворяющее заданным
начальным условиям, называется решением
задачи Коши.
Геометрический смысл решения задачи Коши.
Так как
 ,
то среди интегральных кривых, проходящих
через точку
,
то среди интегральных кривых, проходящих
через точку ,
находят единственную кривую, для которой
прямая с угловым коэффициентом
,
находят единственную кривую, для которой
прямая с угловым коэффициентом ,
является касательной.
,
является касательной.
Линейные дифференциальные уравнения второго порядка. Фундаментальная система решений (фср). Теоремы об общем решении.
Определение.
Линейным однородным дифференциальным
уравнением второго порядка называется
уравнение вида
 (6).
(6).
Определение.
Решения
 и
и уравнения (6) называются линейно-
уравнения (6) называются линейно-
зависимыми, если
 для
для .
Решения
.
Решения и
и уравнения (6)
уравнения (6)
называются
линейно-независимыми, если
 для
для .
.
Определение. Фундаментальной системой решения однородного уравнения (6) называются любые два линейно независимых решения уравнения (6).
Пример.
Для уравнения
 функции
функции


 ,
, являются частными решениями. Пары
решений
являются частными решениями. Пары
решений и
и ,
, и
и ,
, и
и ,
, и
и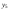 ,
, и
и ,
, и
и ,
, и
и являются линейно-независимыми и образуют
ФСР; пары решений
являются линейно-независимыми и образуют
ФСР; пары решений и
и ,
,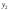 и
и - линейно-зависимые.
- линейно-зависимые.
Теорема (о структуре общего решения линейного однородного уравнения второго порядка).
Пусть
 и
и образуют ФСР уравнения (6), тогда общее
решение уравнения (6) имеет вид
образуют ФСР уравнения (6), тогда общее
решение уравнения (6) имеет вид ,
где
,
где и
и -произвольные постоянные.
-произвольные постоянные.
Определение.
Линейным неоднородным дифференциальным
уравнением второго порядка называется
уравнение вида
 (7), где
(7), где .
.
Этому уравнению
соответствует однородное уравнение

Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Решение линейного однородного уравнения довольно сложная задача,
которая намного упрощается, если коэффициенты уравнения постоянны.
Определение. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
 ,
(8)
,
(8)
где p и q – действительные числа.
Будем искать решение
уравнения в виде функции
 .
Для этого подставим выражения для
.
Для этого подставим выражения для ,
, ,
, в уравнение (8). Так как
в уравнение (8). Так как ,
, ,
то
,
то Поскольку
Поскольку ,
то
,
то (9).
(9).
Определение. Алгебраическое уравнение (9) называется характеристическим уравнением линейного однородного дифференциального уравнения (8).
