
- •Определение дифференциального уравнения. Основные понятия.
- •Дифференциальные уравнения первого порядка.Теорема существования и единственности решения.
- •Дифференциальные уравнения первого порядка с разделяющимися переменными.
- •Линейные дифференциальные уравнения первого порядка.
- •Определение дифференциальных уравнений второго порядка. Основные понятия.
- •Линейные дифференциальные уравнения второго порядка. Фундаментальная система решений (фср). Теоремы об общем решении.
- •Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами их частные решения в зависимости от вида правой части. Метод вариации произвольных постоянных.
- •Определение степенного ряда. Теорема Абеля. Радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов.
- •Численное решение обыкновенных дифференциальных уравнений
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами их частные решения в зависимости от вида правой части. Метод вариации произвольных постоянных.
Определение. Линейным неоднородным дифференциальным уравнением второго порядка с постоянным коэффициентом называется уравнение вида
 ,
(10)
,
(10)
где
 .
.
Рассмотрим два способа решения уравнения (10).
1. Метод вариации
произвольной постоянной заключается
в том, что сначала находят общее решение
 соответствующего однородного уравнения
соответствующего однородного уравнения ,
где функции
,
где функции и
и образуют ФСР однородного уравнения
(8). Общее решение уравнения (10) ищут в
виде
образуют ФСР однородного уравнения
(8). Общее решение уравнения (10) ищут в
виде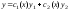 где
где и
и - неизвестные функции. Тогда
- неизвестные функции. Тогда (постоянные
(постоянные и
и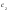 заменяют на функции
заменяют на функции и
и ).
Подберем
).
Подберем и
и так, чтобы
так, чтобы ,
тогда
,
тогда ,
, .
Подставим выражения для
.
Подставим выражения для в (10), получим
в (10), получим .
Таким образом функции
.
Таким образом функции и
и должны удовлетворять системе
должны удовлетворять системе (*). Решим эту систему относительно
(*). Решим эту систему относительно и
и .
Проинтегрировав полученные решения
системы, найдем
.
Проинтегрировав полученные решения
системы, найдем и
и и составим общее решение.
и составим общее решение.
Определение степенного ряда. Теорема Абеля. Радиус сходимости степенного ряда. Дифференцирование и интегрирование степенных рядов.
Определение.
Ряд называется функциональным, если
его члены являются функциями от x,
определенными на (a;b):
 (1).
(1).
Если
 ,
то
,
то (2) – числовой ряд.
(2) – числовой ряд.
Определение.
Если сходится числовой ряд (2), то
функциональный ряд (1) называется
сходящимся в точке
 и точка
и точка называется точкой сходимости ряда (1).
называется точкой сходимости ряда (1).
Определение.
Если сходящийся числовой ряд (2)
расходится, то функциональный ряд (1)
называется расходящимся в точке
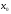 и точка
и точка называется точкой расходимости ряда
(1).
называется точкой расходимости ряда
(1).
Совокупность всех точек сходимости функционального ряда называется его областью сходимости.
Частным случаем функциональных рядов являются степенные ряды.
Определение.
Степенным рядом с центром в точке 0,
называется ряд вида
 (3), где
(3), где – действительные числа.
– действительные числа.
Всякий степенной ряд сходится в своем центре при x=0
Численное решение обыкновенных дифференциальных уравнений
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
![]() ,
где x
– независимая переменная,
,
где x
– независимая переменная,
![]() -i-ая
производная от искомой функции, n
- порядок уравнения. Общее решение ОДУ
n–го
порядка содержит n
произвольных постоянных
-i-ая
производная от искомой функции, n
- порядок уравнения. Общее решение ОДУ
n–го
порядка содержит n
произвольных постоянных
![]() ,
т.е. общее решение имеет вид
,
т.е. общее решение имеет вид![]() .
.
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
