Ранг матрицы.

Рассмотрим kстолбцов иkстрок матрицы, выбранных произвольно. Из элементов, стоящих на пересечении этих строк и столбцов, составим определительk-го порядка. Этот определитель называетсяминором матрицы.

Часть миноров может обращаться в нуль.

Определение. Наивысший из порядков отличных от нуля миноров матрицы называется рангом матрицы.

Для отыскания ранга матрицы вводят понятия элементарных преобразований.

Элементарными преобразованиями называются следующие преобразования:

1. Умножение строки на число, неравное нулю.

2. Сложение строк.

3. Перестановка строк.

4. То же для столбцов.

Теорема. Элементарные преобразования не меняют ранга матрицы.

На основании этой теоремы матрица приводится к виду:

Звездочкой обозначены элементы, значения которых для нас безразличны.

Отсюда видно, что Rg A = r.

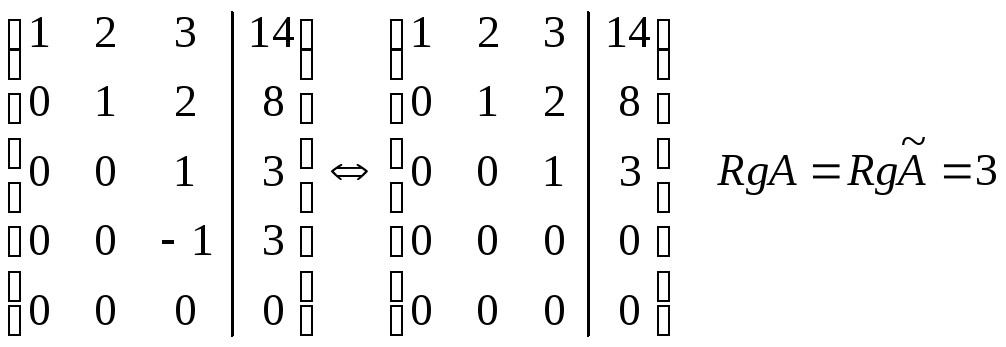
П р и м е р.Определить ранг матрицы.

(2)-(1)∙2 (2)∙(-1) (3)-(2)∙5 (3):(-18)

(3)-(1)∙3 (3)∙(-1)

RgA = 3

Рассмотрим систему mлинейных уравнений сnнеизвестными.

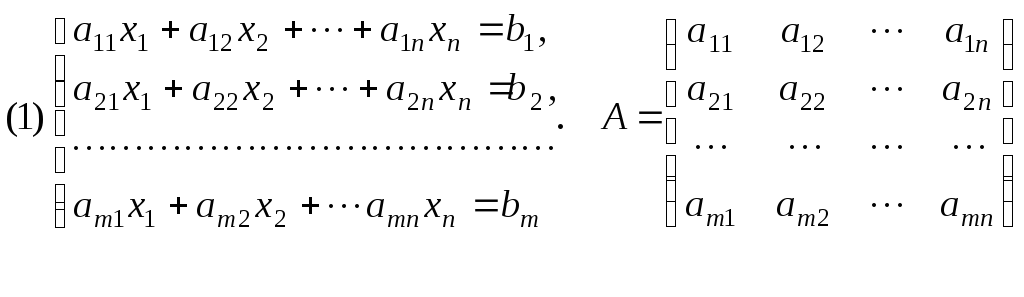
Если число уравнений равно числу неизвестных (m=n), то система имеет единственное решение, когда определитель системы ∆ ≠ 0. Если ∆ = 0, то система либо имеет бесконечное множество решений, либо не имеет решений вообще.

Выясним условие совместности системы. Рассмотрим матрицу

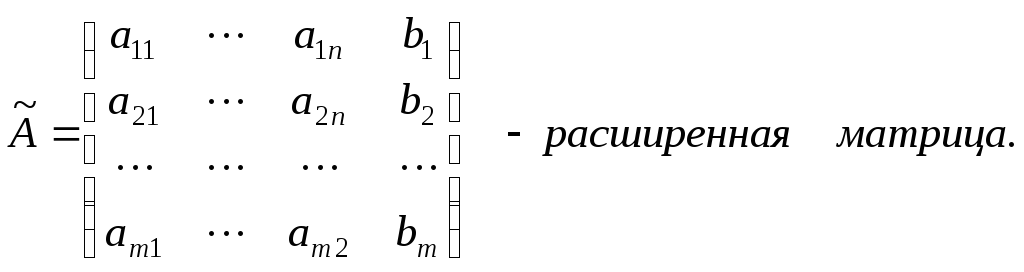
Теорема Кронекера–Капелли.Система (1) имеет хотя бы одно решение в том и только томслучае, когда ранг матрицы системы равен рангу расширенной матрицы

Пр и м е р ы. Проверить, будет ли совместна система и в случае совместности решить.

1. x₁+ 3x₂+ 5x₃+ 7x₄+ 9x₅= 1,x₁– 2x₂+ 3x₃– 4x₄+ 5x₅= 2, 2x₁+11x₂+ 12x₃+ 25x₄+ 22x₅= 4.

(2) - (1) (3) + (2)

(3) – (1)∙2

RgA= 2,RgĂ = 3,система не совместна.

2. 3x₁ + 2x₂ + x₃ = 10, x₁ + 2x₂ + 3x₃ = 14, x₁ + x₂ + x₃ = 6, 2x₁ + 3x₂ – x₃ = 5, x₁ + x₂ = 3.

(2) – (1)∙ 3 (2):(-4) (3) + (4) (3) – (1) (4) – (1)∙2 (5) – (1)

(4): (-3) (3) + (4) (3)→(5)

Запишем получившуюся систему.

x₁ + 2x₂ + 3x₃ = 14, x₃ = 3, x₂ = 8 – 2x₃ = 2, x₁ = 14 – 2x₂ – 3x₃ = 14- 4 -6 = 1

x₂ + 2x₃ = 8, x₃ = 3.

3. 2x₁ + x₂ – x₃ = 5 x₁ – 2x₂ + 2x₃ = -5 7x₁ + x₂ – x₃ = 10.

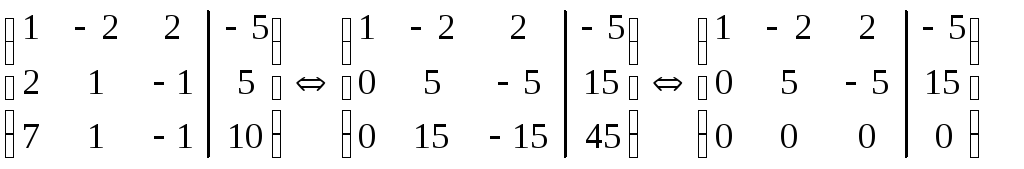
x₁ – 2x ₂ + 2x₃ = -5, x₂ = 3 + x₃, x₂ - x₃ = 3. x₁ = -5 + 2x₂– 2x₃ = -5 + 6 + 2x₃– 3x₃= 1.

Ответ ( 1; 3 + х₃; х₃ ) – бесконечное множество решений (ранг матриц равен двум, а число неизвестных равно трем, т.е. число неизвестных больше ранга матрицы).