
- •1.Вектор в геометрии — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора. Сложение
- •Векторное произведение
- •Смешанное произведение
- •9. Пучок плоскостей — уравнение любой п., проходящей через линию пересечения двух плоскостей
- •13. Цилиндрические поверхности
- •[Править]Конические поверхности
- •[Править]Поверхности вращения
- •Матричные операции
- •С помощью матрицы алгебраических дополнений
- •Метод Жордана: Алгоритм
- •Аксиомы линейного пространства
- •23. Базис. Размерность
- •Свойства нормы
- •Собственные значения и собственные векторы линейного оператора.
1.Вектор в геометрии — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора. Сложение
Операцию сложения геометрических векторов можно определить по разному, в зависимости от ситуации и типа расматриваемых векторов:
Правило
треугольника.
Для сложения двух векторов ![]() и
и ![]() по
правилу треугольника оба
эти вектора переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
по
правилу треугольника оба
эти вектора переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограммаоба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
А
модуль (длину) вектора суммы ![]() определяют
по теореме
косинусов
определяют
по теореме
косинусов ![]() где
где ![]() —
угол между векторами, когда начало
одного совпадает с концом другого. Так
же используется формула
—
угол между векторами, когда начало
одного совпадает с концом другого. Так
же используется формула ![]() теперь
—
угол между векторами выходящими из
одной точки.
теперь
—
угол между векторами выходящими из
одной точки.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Векторное произведение
Векторным
произведением вектора ![]() на
вектор
на
вектор ![]() называется
вектор
называется
вектор ![]() ,
удовлетворяющий следующим требованиям:
,
удовлетворяющий следующим требованиям:
длина вектора равна произведению длин векторов и на синус угла φ между ними
![]()
вектор ортогонален каждому из векторов и
вектор направлен так, что тройка векторов
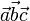 является правой.
является правой.
Обозначение: ![]()
Геометрически
векторное произведение ![]() есть
ориентированная площадь параллелограмма,
построенного на векторах
есть
ориентированная площадь параллелограмма,
построенного на векторах ![]() ,
представленная псевдовектором,
ортогональным этому параллелограмму.
,
представленная псевдовектором,
ортогональным этому параллелограмму.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
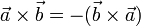
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть

Векторное произведение обладает распределительным свойством:

Смешанное произведение
Сме́шанное
произведе́ние ![]() векторов
векторов ![]() — скалярное
произведение вектора
на векторное
произведение векторов
и
:
— скалярное
произведение вектора
на векторное
произведение векторов
и
:
![]()
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объём параллелепипеда, построенного на векторах .
Система векторов A1, A2,...,An называется линейно зависимой, если существует ненулевой набор чисел λ1, λ2,...,λn, при котором линейная комбинация векторов λ1*A1+λ2*A2+...+λn*An равна нулевому вектору, то есть система уравнений: A1x1+A2x2+...+Anxn =Θ имеет ненулевое решение. Набор чисел λ1, λ2,...,λn является ненулевым, если хотя бы одно из чиселλ1, λ2,...,λn отлично от нуля.
Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой.
Критерий линейной зависимости векторов
Необходимым и достаточным условием линейной зависимости двух
векторов является их коллинеарность.
2. Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается каккоммутативная и линейная по каждому сомножителю.
Свойства
скалярного произведения: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости[1].
Необходимым и достаточным условием линейной зависимости трех
векторов является их компланарность.
Любые четыре вектора линейно зависимы. Базисом в пространстве называется любая
упорядоченная тройка некомпланарных векторов. Базис в пространстве позволяет однозначно сопоставить каждому вектору
упорядоченную тройку чисел – коэффициенты представления этого вектора в виде
линейной комбинации векторов базиса. Наоборот, каждой упорядоченной тройке
чисел
![]() при
помощи базиса
при
помощи базиса
![]()
мы
сопоставим вектор
![]() ,
если
,
если
составим
линейную комбинацию
![]()
Ортогональный базис называется ортонормированным, если его
векторы по длине равны единице. Для ортонормированного базиса в пространстве
часто
используют обозначения
![]() .
.
Теорема: В ортонормированном базисе координаты векторов есть
соответствующие ортогональные проекции этого вектора на направления
координатных векторов. Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c - левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат OX и OY. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. Вправосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси OY вверх, ось OXсмотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1).
если
векторы ![]() и
и ![]() относительно
ортонормированного базиса на плоскости
имеют координаты
относительно
ортонормированного базиса на плоскости
имеют координаты ![]() и
и ![]() соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
соответственно,
то скалярное произведение этих векторов
вычисляется по формуле
![]()
4. Векторное произведение двух векторов а и b - это операция над ними, определенная лишь в трехмерном пространстве, результатом которой являетсявектор со следующими
свойствами:
Геометрическим
смыслом векторного произведения векторов
является площадь параллелограмма,
построенного на векторах. Необходимым
и достаточным условием коллинеарности
ненулевого вектора ![]() и
вектора
и
вектора ![]() является
существование такого числа
является
существование такого числа ![]() ,
которое удовлетворяет равенству
,
которое удовлетворяет равенству ![]() .
.
Если
два вектора ![]() и
и ![]() определены
своими прямоугольными
декартовыми координатами,
а говоря точнее — представлены
вортонормированном
базисе
определены
своими прямоугольными
декартовыми координатами,
а говоря точнее — представлены
вортонормированном
базисе
![]()
![]()
а система координат правая, то их векторное произведение имеет вид
![]()
Для запоминания этой формулы удобно использовать определитель:
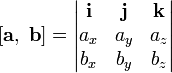
5.
Сме́шанное
произведе́ние ![]() векторов
векторов ![]() — скалярное
произведение вектора
на векторное
произведениевекторов
и
— скалярное
произведение вектора
на векторное
произведениевекторов
и ![]() :
:
![]() .
.
Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр(точнее — псевдоскаляр).
Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами .
При перестановке двух множителей смешанное произведение изменяет знак на противоположный:
При циклической (круговой) перестановке множителей смешанное произведение не изменяется:
![]()
Смешанное произведение линейно по любому множителю.
Смешанное
произведение ![]() равно
нулю тогда и только тогда, когда
векторы
равно
нулю тогда и только тогда, когда
векторы ![]() компланарны.
компланарны.
1. Условие компланарности векторов: три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Тройка векторов, содержащая пару коллинеарных векторов, компланарна.
Смешанное произведение компланарных векторов
 .
Это — критерий компланарности трёх
векторов.
.
Это — критерий компланарности трёх
векторов.Компланарные векторы — линейно зависимы. Это — тоже критерий компланарности.
Существуют действительные числа
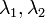 такие,
что
такие,
что 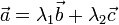 для
компланарных
,
за исключением случаев
для
компланарных
,
за исключением случаев  или
или  .
Это — переформулировка предыдущего
свойства и тоже критерий компланарности.
.
Это — переформулировка предыдущего
свойства и тоже критерий компланарности.В 3-мерном пространстве 3 некомпланарных вектора образуют базис. То есть любой вектор
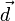 можно
представить в виде:
можно
представить в виде: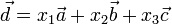 .
Тогда
.
Тогда 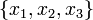 будут
координатами
в
данном базисе.
будут
координатами
в
данном базисе.
Смешанное
произведение
в
правой декартовой системе координат
(в ортонормированном базисе)
равно определителю
матрицы,
составленной из векторов ![]() и
:
и
:
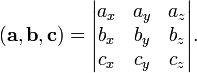
6. Общее уравнение (полное) плоскости
![]()
где ![]() и
и ![]() —
постоянные, причём
—
постоянные, причём ![]() и
и ![]() одновременно
не равны нулю; в векторной форме:
одновременно
не равны нулю; в векторной форме:
![]()
где ![]() —
радиус-вектор точки
—
радиус-вектор точки ![]() ,
вектор
,
вектор ![]() перпендикулярен
к плоскости (нормальный
вектор).Направляющие косинусы вектора
перпендикулярен
к плоскости (нормальный
вектор).Направляющие косинусы вектора ![]() :
:
![]()
![]()
![]()
Если
один из коэффициентов в уравнении
плоскости равен нулю, уравнение
называется неполным.
При ![]() плоскость
проходит через начало
координат,
при
плоскость
проходит через начало
координат,
при ![]() (или
(или ![]() ,
, ![]() )
П. параллельна оси
)
П. параллельна оси ![]() (соответственно
(соответственно ![]() или
или ![]() ).
При
).
При ![]() (
(![]() ,
или
,
или ![]() )
плоскость параллельна
плоскости
)
плоскость параллельна
плоскости ![]() (соответственно
(соответственно ![]() или
или ![]() ).
).
Уравнение плоскости в отрезках:
![]()
где ![]() ,
, ![]() ,
, ![]() —
отрезки, отсекаемые плоскостью на
осях
—
отрезки, отсекаемые плоскостью на
осях ![]() и
.
и
.
Уравнение плоскости, проходящей через точку
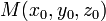 перпендикулярно
вектору нормали
перпендикулярно
вектору нормали 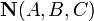 :
:
![]()
в векторной форме:
![]()
(смешанное произведение векторов), иначе

Нормальное (нормированное) уравнение плоскости
![]()
Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
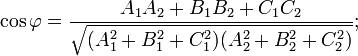
Если в векторной форме, то
![]()
Плоскости параллельны, если
![]() или
или ![]() (Векторное
произведение)
(Векторное
произведение)
Плоскости перпендикулярны, если
![]() или
или ![]() .
(Скалярное произведение)
.
(Скалярное произведение)
7. Уравнение
плоскости, проходящей через три заданные
точки ![]() , не
лежащие на одной прямой:
, не
лежащие на одной прямой:
![]()
8.Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, чторасстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Отклонение точки
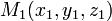 от
плоскости заданной нормированным
уравнением
от
плоскости заданной нормированным
уравнением 
![]()
![]() ,если
,если ![]() и
начало координат лежат по разные стороны
плоскости, в противоположном случае
и
начало координат лежат по разные стороны
плоскости, в противоположном случае ![]() .
Расстояние от точки до плоскости равно
.
Расстояние от точки до плоскости равно ![]()
Расстояние
 от
точки
от
точки 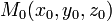 ,
до плоскости, заданной уравнением
,
до плоскости, заданной уравнением 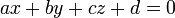 ,
вычисляется по формуле:
,
вычисляется по формуле:
![]()
