Особенности нелинейных САУ.

Система автоматического управления (САУ) является нелинейной, если хотя бы один ее конструктивный элемент (или одно ее алгоритмическое звено) описывается нелинейным уравнением. Особенности нелинейных САУ.

1. они не подчиняются принципу наложения (суперпозиции), а характер и показатели переходного процесса зависят от величины внешнего воздействия или начального отклонения. Например, при малом начальном отклонении x1(0), меньшем некоторого критического значения хкр, переходный процесс может быть апериодическим), а при большом начальном отклонении х2(0) > хкр – колебательным.

2. зависимость условий устойчивости от величины внешнего воздействия: САУ, устойчивая при одних значениях начального отклонения, оказывается неустойчивой при других его значениях. В связи с этим для нелинейных САУ применяют понятия «устойчивость (неустойчивость) в малом», «устойчивость (неустойчивость) в большом», «устойчивость в целом». Система устойчива в малом, если она устойчива только при малых начальных отклонениях. Система устойчива в большом, если она устойчива при больших начальных отклонениях. Система устойчива в целом, если она устойчива при любых отклонениях. 3) Специфической особенностью нелинейных САУ является также режим автоколебаний. Автоколебания - это устойчивые собственные колебания, возникающие из-за нелинейных свойств системы. Режим автоколебаний нелинейной системы принципиально отличается от колебания линейной системы на границе устойчивости. В линейной системе при малейшем изменении ее параметров колебательный процесс становится либо затухающим, либо расходящимся. Автоколебания же являются устойчивым режимом: малые изменения параметров системы не выводят ее из этого режима. Амплитуда автоколебаний хт не зависит от начальных условий и уровня внешних воздействий. 4) при затухающих колебаниях переходного процесса в нелинейных системах возможно изменение периода колебаний.

Особенности устойчивости нелинейных САУ.

Особенность нелинейных САУ - САУ, устойчивая при одних значениях начального отклонения, оказывается неустойчивой при других его значениях. Для нелинейных САУ применяют понятия «устойчивость (неустойчивость) в малом», «устойчивость (неустойчивость) в большом», «устойчивость в целом». Система устойчива в малом, если она устойчива только при малых начальных отклонениях. Система устойчива в большом, если она устойчива при больших начальных отклонениях. Система устойчива в целом, если она устойчива при любых отклонениях.

Исследование нелинейных САУ на фазовой плоскости

]. Фазовым пространством называется пространство, по осям координат которого отложены переменные, характеризующие состояние динамической системы. Если движение системы описывается дифференциальным уравнением n-го порядка, то состояние этой системы в любой момент времени можно характеризовать некоторой точкой n-мерного фазового пространства, по осям которого отложены координата системы и (n-1) ее производных. Точка, характеризующая состояние системы в фазовом пространстве, называется изображающей точкой. При движении системы изображающая точка описывает в фазовом пространстве некоторую кривую, называемую фазовой траекторией. Каждому определенному переходному процессу в фазовом пространстве соответствует определенная фазовая траектория. Начальное положение изображающей точки определяется начальными условиями. В установившемся равновесном состоянии системы все производные рассматриваемой переменной равны нулю. Соответствующие этому точки фазового пространства находятся в покое и называются особыми точками. Совокупность фазовых траекторий для всевозможных начальных отклонений называется фазовым портретом системы. По виду фазового портрета системы определяют особые точки и особые траектории, исследуют устойчивость системы и оценивают качество процесса управления.

Метод фазовой плоскости используется для исследования нелинейных систем, линейная часть которых описывается дифференциальным уравнением не выше второго порядка, а нелинейный элемент может быть любым. Метод заключается в том, что из уравнений состояния исключается время и определяются уравнения фазовых кривых. Задача значительно упрощается, если нелинейный элемент обладает кусочно-линейной характеристикой. Тогда фазовое пространство разбивается на ряд областей, где работа нелинейной системы описывается обыкновенными линейными уравнениями, на основании которых строятся фазовые траектории. Непрерывность движения изображающей точки на фазовом пространстве (переход из одной области в другую) обеспечивается "сшиванием" по линиям переключения в соответствии с видом нелинейности. При исследовании нелинейных систем высокого порядка их аппроксимируют системами второго порядка с эквивалентным запаздыванием. Уравнение фазовой траектории может быть получено из уравнений состояния

 (7.9)

где: x₁, x₂ - координата системы и ее производная; f(x₁;x₂) - нелинейная функция.  Разделив второе из уравнений (7.9) на первое, получим уравнение фазовой траектории, в котором отсутствует время t в явном виде:

 (7.10)

Решение уравнения (7.10) x₂ = F(x₁) изображается на фазовой плоскости (x₁;x₂). По оси абсцисс откладывается сама координата x₁, а по оси ординат откладывается ее первая производная x₂. Каждой совокупности начальных условий (x₁₀, x₂₀) соответствует свое решение и своя фазовая траектория. Семейство фазовых траекторий характеризует все возможные виды переходных процессов в данной системе управления при любых начальных условиях и образует ее фазовый портрет. Основные свойства фазовых траекторий вытекают из выражения (7.10): 1) если F(x₁;x₂) определена и непрерывна в некоторой области и имеет непрерывные частные производные по своим аргументам, то через каждую точку фазовой плоскости, за исключением особых точек, проходит единственная фазовая траектория. Это означает, что фазовые траектории не пересекаются между собой; 2) при x₂=>0 координата x₁ должна возрастать, поэтому в верхней фазовой полуплоскости при возрастании времени t изображающая точка движется слева направо. Соответственно в нижней полуплоскости движение происходит справа налево. Направление движения на траекториях показывают стрелками; 3) в точках, где x₂ = 0 и F(x₁;x₂) не равно 0, фазовые траектории пересекают ось абс-цисс под прямым углом. Ось ординат фазовые траектории могут пересекать под любым углом. В большинстве своем решение уравнения (7.10) может быть получено простым интегрированием, но если переменные x₁ и x₂ не разделяются, то фазовые траектории можно построить приближенным графоаналитическим методом, например, методом изоклин [2,4].  Изоклиной называется такая линия, во всех точках пересечения которой с фазовыми траекториями, последние наклонены под одним и тем же углом α_i к оси абсцисс, т.е. с_i =dx₂/dx₁ и arctg c_i = α_i. Уравнение изоклины получается из уравнения (7.10) подстановкой

из которого получается уравнение изоклины x₂ = φ(x₁, c_i ). Задавая различные значения с_i наклона касательных к фазовым траекториям, пересекающим эти изоклины, строят семейство изоклин, которые используются для построения фазовых траекторий (рис. 7.9). В качестве примера на рис. 7.8 на изоклинах отмечены наклоны фазовых траекторий к оси абсцисс и построена фазовая траектория, исходящая из точки М_о.

  Рис. 7.9. Фазовая траектория нелинейной САУ

Особенностью фазовых траекторий нелинейных САУ является то, что кроме особых точек на фазовом портрете могут появляться особые траектории [2,3,6,13]. На рис.7.3 показаны предельные циклы: неустойчивый и устойчивый. К этим предельным циклам стремятся изображающие точки при различных начальных отклонениях по различным фазовым траекториям. Устойчивый предельный цикл соответствует автоколебаниям системы. Размеры предельного цикла представляют амплитуды колебаний самой величины x₁ и скорости ее изменения x₂. Пересечение траектории устойчивого предельного цикла с осью абсцисс определяет амплитуду автоколебаний А_о, а пересечение с осью ординат определяет величину произведения амплитуды на частоту колебаний А_оω_о.

.

Основные понятия теории устойчивость нелинейных САУ

Для нелинейных САУ применяют понятия «устойчивость (неустойчивость) в малом», «устойчивость (неустойчивость) в большом», «устойчивость в целом». Система устойчива в малом, если она устойчива только при малых начальных отклонениях. Система устойчива в большом, если она устойчива при больших начальных отклонениях. Система устойчива в целом, если она устойчива при любых отклонениях.

Общая структурная схемаимпульсной САУ

Отличительной особенностью импульсной системы является преобразование непрерывного сигнала x(t) в последовательность импульсов z(t). Поэтому для описания импульсной системы в ее структуру вводят импульсное звено, которому и приписывают описание этого процесса. Остальные компоненты импульсной системы специфических свойств не имеют, они рассматриваются как непрерывная часть системы (т.е. совокупность элементов с непрерывными характеристиками преобразования) и могут быть описаны с использованием методов теории обыкновенных линейных систем.

Обобщенная структура импульсной системы, составленная на основе описанного подхода, приведена на рис. 28. Импульсному звену ИЗ приписывается преобразование непрерывного сигнала x(t) в последовательность импульсов z(t), которая поступает на непрерывную часть импульсной системы с передаточной функцией W_н(p).

В исследуемой системе импульсное звено может быть включено в любой части системы. Путем преобразования структуры исследуемой системы ее всегда можно свести к структуре, представленной на рис. 28. При этом математическое описание импульсной системы сводится к математическому описанию функции преобразования для импульсного звена. Решение последней задачи будет зависеть от способа наложения информации квантованного сигнала на несущие импульсы.

Математическое описание импульсных САУ

Обобщенная структура импульсной системы, составленная на основе описанного подхода, приведена на рис. 28. Импульсному звену ИЗ приписывается преобразование непрерывного сигнала x(t) в последовательность импульсов z(t), которая поступает на непрерывную часть импульсной системы с передаточной функцией W_н(p).

В исследуемой системе импульсное звено может быть включено в любой части системы. Путем преобразования структуры исследуемой системы ее всегда можно свести к структуре, представленной на рис. 28. При этом математическое описание импульсной системы сводится к математическому описанию функции преобразования для импульсного звена. Решение последней задачи будет зависеть от способа наложения информации квантованного сигнала на несущие импульсы.

Решетчатые функции и разностные уравнения.

Величины, описывающие поведение автоматических систем, представляют собой функции времени. Математическое исследование дискретных систем существенно упрощается в том случае, когда все величины рассматриваются в дискретные равноотстоящие моменты времени.

Решетчатая функциявремени , или в сокращенной записи  - это математическая функция,значения которой определены в дискретные равноотстоящие друг от другамоменты времени ,

где n - целое положительное число 0, 1, 2 ...,

Т -период дискретности.

То есть решетчатая функция представляет собой числовую последовательность:

, , , , …,

Если период дискретности T задан, то решетчатая функция однозначно формируется из исходной непрерывной . Обратная задача - формирование непрерывной функции из решетчатой - не может быть решена однозначно без дополнительных сведений о поведении функции в интервале между точками , так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.Непрерывные функции, проходящие через дискреты заданной решетчатой функции, называют огибающими. Их бесконечно много (рис.21.3).

Для суждения о характере поведения непрерывной функции в интервалах между дискретными моментами времени водится понятие смещенной решетчатой функции , которая представляет собой числовуюпоследовательность:

, , , , …, ,

где - постоянное число, называемое смещением, выбираемое из интервала .

Для удобства записи вводят переменную – относительное время . В этом случае непрерывной функции в относительном времени будет соответствовать решетчатая функция или смещенная решетчатая функция , обозначаемая сокращенно .

Аналогами производных и интегралов непрерывных функций для решетчатых функций являются конечные разности и конечные суммы.

Конечные разности решетчатых функций бывают двух видов: прямые(упреждающие) и обратные (отстающие).

Первой прямой конечной разностью функции называется решетчатая функция вида .

Перваяобратная конечная разность.

Вторую прямую конечную разность определяют как разность двух первых разностей .

Вторая обратная конечная разность .

Разности произвольного порядка k определяются при помощи рекуррентных соотношений:

где k = 1, 2, 3, ........

Общее решение однородного разностного уравнения при некратных корнях характеристического уравнения может быть записано следующим образом:

где z_i - корни характеристического уравнения

C_i - постоянные коэффициенты.

Для получения возможности исследования решений разностных уравнений в общем виде широко используются дискретное преобразование Лапласа, z-преобразование, -преобразование, а также частотные методы.

21.2. Дискретное преобразование Лапласа

Дискретное преобразование Лапласа определяется следующим соотношением:

а) для решетчатой функции

б) для смещенной решетчатой функции

где - оператор Лапласа;

- абсцисса абсолютной сходимости.

Для существования изображений по Лапласу , необходимо, чтобы степенные ряды в выражениях для , сходились. Условием сходимости является .

Дискретное преобразование Лапласа содержит трансцендентный сомножитель , из-за которого изображения и соответствующие передаточные функции становятся иррациональными функциями аргумента р, что создает определенные трудности при их использовании. Поэтому с целью получения передаточных функций дискретных систем в дробно-рациональной форме целесообразна определенная замена аргументов ().

21.3. Z-преобразование

Z-преобразование связано дискретным преобразованием Лапласа посредством подстановки .

Z-преобразованиемрешетчатой функции называется функция комплексного аргумента z, определяемая выражением

для смещенной решетчатой функции

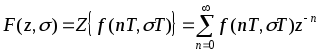
Главное достоинство и удобство z-преобразования заключается в том, что сама запись z-изображения указывает простой способ выполнения прямого и обратного преобразования:

- чтобы по известной функции времени найти ее z-изображение, необходимо лишь каждое дискретное значение умножить на , а затем свернуть получившийся степенной ряд в конечную сумму;

- чтобы по известному изображению найти соответствующий сигнал , необходимо представить изображение в виде степенного ряда по убывающим степеням , получающиеся при этом числовые коэффициенты ряда и есть дискретные значения сигнала .