Zadanie_Kratnye_integraly_MTUSI_2013g

	Вариант 11
1.	Расставить пределы интегрирования двумя способами в двойном интеграле
	∫∫ f (x, y)dxdy в декартовых координатах для области D : y2 = 2 − x, y = x.
	D
2.	Найти массу неоднородной пластины D : y =0, x2 =1− y, если поверхностная
плотность в каждой ее точке µ(x, y)=3 − x − y.
3.	Найти статический момент однородной пластины D : x2 + y2 −2y ≤0,

x2 + y2 + 2x ≥0, x ≤0, относительно оси Ox , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область V :
6y = x2 + z2 , y =8.
5.	Найти момент инерции однородного тела относительно оси Ox , занимающего

область V : x2 = y2 + z2 , y2 + z2 =1, x =0.

6.Найти объем тела, ограниченного поверхностями: z = x, z = 4 − y2 , x =0.

7.Вычислить непосредственно и с помощью формулы Грина:

∫		2	+	y2		2	dy, где L −контур треугольника ABC :	A(1;1), B(2;2),
	3 x			2	dx +(x − y)
L

C(1;3).

8.Вычислите поток векторного поля F =(z +1)xi + yj +(z − x2 )k через внешнюю

сторону границы области, ограниченной поверхностями z = 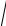4 − x2 − y2 и z =1. 9. Найдите циркуляцию векторного поля F = yzi + xzj +(x − y)k вдоль эллипса,

образованного пересечением эллипсоида x2 + y2 + 2z2 = 2 с плоскостью x + y =0.

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его

скалярный или векторный потенциал и сделать проверку потенциала: a = zj − yk.

Вариант 12

1. Расставить пределы интегрирования двумя способами в двойном интеграле

∫∫ f (x, y)dxdy в декартовых координатах для области D : x = 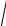2 − y2 , x = y2 , y ≥0.

	D
2.	Найти массу неоднородной пластины D : y = x2 , x = y2 , если поверхностная
плотность в каждой ее точке µ(x, y)=3x + 2y +6.
3.	Найти статический момент однородной пластины D : x2 + y2 −2y ≥0,
x2 + y2 −2x ≤0, y ≥0,относительно оси Oy , используя полярные координаты.
4.	Найти координаты центра масс однородного тела, занимающего область V :
8x = y2 + z2 , x = 1		2	.
5.	Найти момент инерции однородного тела относительно оси Ox , занимающего
область V : x = y2 + z2 , y2 + z2 =1, x =0.
6.	Найти объем тела, ограниченного поверхностями: (x −1)2 + y2 =1, z =0,
	x + y + z = 4 .

7. Вычислить непосредственно и с помощью формулы Грина:

∫2(x2 + y2 )dx +(x + y)2 dy , где L −контур треугольника ABC : A(1;1), B(2;2),

L

C(1;3).

8.Вычислите поток векторного поля F = xi + y2 j + 2zk через внешнюю сторону

границы области, ограниченной поверхностями y = 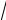x , x + z =1, y =0 и z =0 . 9. Вычислить модуль криволинейного интеграла (циркуляцию)

∫(x2 −3z)dx +(5y +3)dy +(z +7x)dz , где C − линия пересечения эллиптического

C

цилиндра x2 + z2 =1 с плоскостью 5x −10y −6z =0. 16 25

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = x2 (xi −3yj ).

Вариант 13

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области D : y ≥0, x + 2y −12= 0,

	D
y = lg x.
2.	Найти массу неоднородной пластины D : y = x2 , y = 4, если поверхностная
плотность в каждой ее точке µ(x, y)= 2x +5y +10.
3.	Найти статический момент однородной пластины D : x2 + y2 + 2y =0,
x2 + y2 + y =0, x ≤0, относительно оси Ox , используя полярные координаты.
4.	Найти координаты центра масс однородного тела, занимающего область V :
2x = y2 + z2 , y2 + z2 = 4, x =0.
5.	Найти момент инерции однородного тела относительно оси Oz , занимающего

область V : z2 = x2 + y2 , z =3.

6.Найти объем тела, ограниченного поверхностями: z =1− x2 , z =1− y2 , z =0 .

7.Вычислить непосредственно и с помощью формулы Грина:

∫(xy + x + y)dx +(xy + x − y)dy , где L − окружность x2 + y2 = R2 .

L

8.Вычислите поток векторного поля F = y3i +(y − x) j + z2k через внешнюю сторону границы области, ограниченной поверхностями z = x2 + y2 и z = 4 .

9. Найдите циркуляцию векторного поля F = yi + y2 j +(z − x)k по контуру,

x =cost,

заданному параметрически: y =cost,

z =sint.

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = 2x(x(y − z)i +(−y2 )j + z2k ).

Вариант 14

1. Расставить пределы интегрирования двумя способами в двойном интеграле

∫∫ f (x, y)dxdy в декартовых координатах для области D : x ≤0, y ≥1, y ≤3, y = −x.

D

2.Найти массу неоднородной пластины D : x =0, y =0, x + y =1, если поверхностная плотность в каждой ее точке µ(x, y)= 2x2 + y2.

3.Найти статический момент однородной пластины D : x2 + y2 −2x =0,

x2 + y2 − x =0, y ≥0, относительно оси Oy , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область V :
4y = x2 + z2 , x2 + z2 =16, y =0.
5.	Найти момент инерции однородного тела относительно оси Oz , занимающего

область V : z = x2 + y2 , z =3.

6.Найти объем тела, ограниченного поверхностями: x2 + y2 + z2 = 25, 3 ≤ z ≤ 4.

7.Вычислить непосредственно и с помощью формулы Грина: ∫(x + y)dx −(x − y)dy ,

L

где L − контур треугольника ABC : A(1;1), B(2;2), C (1;3).

8. Вычислите поток векторного поля F = xzi + yzj +(z2 −1)k через внешнюю сторону границы области, ограниченной поверхностями z = 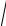x2 + y2 , x2 + y2 =1, и z = 2

( x2 + y2 ≤1).

9. Вычислить модуль криволинейного интеграла (циркуляцию)

∫(5x +3)dx +(y2 −3z)dy +(z +7 y)dz , где C − линия пересечения эллиптического

C

цилиндра y2 + z2 =1 с плоскостью 10x −5y +6z =0. 16 25

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = y2 (yj −3zk ).

Вариант 15

1. Расставить пределы интегрирования двумя способами в двойном интеграле

∫∫ f (x, y)dxdy в декартовых координатах для области D : y = 0, y ≥ x, y = −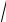2 − x2 .

	D
2.	Найти массу неоднородной пластины D : x =0, y2 =1− x, если поверхностная
плотность в каждой ее точке µ(x, y)= 2 − x − y.
3.	Найти статический момент однородной пластины D : x2 + y2 + 2y =0,
x2 + y2 + y =0, x ≥0, относительно оси Ox , используя полярные координаты.
4.	Найти координаты центра масс однородного тела, занимающего область V :
8x = y2 + z2 , x = 2.
5.	Найти момент инерции однородного тела относительно оси Oy , занимающего
область V : y2 = x2 + z2 , x2 + z2 = 4, y =0.
6.	Найти объем тела, ограниченного поверхностями: z = 4xy, z =0, y ≥ 2, x + y = 4.
7.	Вычислить непосредственно и с помощью формулы Грина:

∫(1− x2 )ydx + x(1+ y2 )dy , где L − окружность x2 + y2 = R2 .

L

8.Вычислите поток векторного поля F = xy3i + y2 j + zk через внешнюю сторону границы области, ограниченной поверхностями x2 + z2 = 2z , y = −1 и y =1.

9.Найдите циркуляцию векторного поля F =(z2 − y2 )i +(x2 − z2 ) j +(y2 − x2 )k по

контуру, образованному пересечением поверхностей x2 + y2 = 4x и x + y + z =0 .

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = z(yzi + xzj + 2xyk ).

Вариант 16

1. Расставить пределы интегрирования двумя способами в двойном интеграле

∫∫ f (x, y)dxdy в декартовых координатах для области D : y ≥0, x = 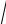y, y = 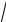6 − x2 .

D

2.

Найти массу неоднородной пластины D : y =

,

y = x, если поверхностная

x

плотность в каждой ее точке µ(x, y)= 2 − x − y.

3.

Найти статический момент однородной пластины D : x2 + y2 −2y =0,

x2 + y2 − y =0,

x ≥0,относительно оси Ox , используя полярные координаты.

4.

Найти координаты центра масс однородного тела, занимающего область V :

z =36.

z =9 x2 + y2 ,

5.

Найти момент инерции однородного тела относительно оси

Oy , занимающего

область V : 2y = x2 + z2 ,

y = 2.

6.

Найти объем тела, ограниченного поверхностями:

z =8 − y2 ,

z =0, x2 + y2 = 4.

7.

Вычислить непосредственно и с помощью формулы Грина:

∫

2

2

(xy + x + y)dx +(xy + x − y)dy , где L −эллипс

x

+

y

=1.

2

2

L

a

b

8.

Вычислите поток векторного поля F =(x + y2 )i + xzj + k через внешнюю сторону

границы области, ограниченной поверхностями x2 + y2 = 4x , z =0 и z =1.

9.

Вычислить криволинейный интеграл (циркуляцию)

∫(3x3 −2y3 + z)dx +(3y3 − x2 y − z2 x)dy +(xyz)dz , где C − линия пересечения

C

сферической поверхности

x2 + y2 + z2 =12 с параболоидом z = x2 + y2 . Линия

проходится по часовой стрелке, если смотреть от начала координат Oz .

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = yz2 (yzi + 2xzj +3xyk ).

	Вариант 17
1.	Расставить пределы интегрирования двумя способами в двойном интеграле
	∫∫ f (x, y)dxdy в декартовых координатах для области D : y = −x, y2 = x + 2.
	D
2.	Найти массу неоднородной пластины D : y = x2 −1, y =1, если поверхностная
плотность в каждой ее точке µ(x, y)=3x2 + 2y2 +1.
3.	Найти статический момент однородной пластины D : x2 + y2 −2y =0,

x2 + y2 − y =0, x ≤0, относительно оси Ox , используя полярные координаты. 4. Найти координаты центра масс однородного тела, занимающего область V : z =3(x2 + y2 ), x2 + y2 =9, z =0.

5.	Найти момент инерции однородного тела относительно оси	Ox , занимающего
область V : x2 = y2 + z2 , x = 2.
6.	Найти объем тела, ограниченного поверхностями: z2 = y, z2 = 4 − y, x =0,
	x + y = 4.
7.	Вычислить непосредственно и с помощью формулы Грина: ∫L	xdy − ydx
		x2 + y2 , где

L −контур прямоугольника 0 ≤ x ≤ 2, 1≤ y ≤5.

8. Вычислите поток векторного поля F = xzi +(x + z) j + xyk через внешнюю сторону границы области, ограниченной поверхностями x2 + y2 + z =7 и z =3.

9. Найдите циркуляцию векторного поля F = 2xi − z2 j + yk по контуру, заданному

x =cost,

параметрически: y =3sint,

z = 2cost −sint +1.

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его

скалярный или векторный потенциал и сделать проверку потенциала: a = z(xi − yj ).

Вариант 18

1. Расставить пределы интегрирования двумя способами в двойном интеграле

∫∫ f (x, y)dxdy в декартовых координатах для области D : y = 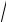4 − x2 , x ≥0, x =1,

D

y = 0 .

2.Найти массу неоднородной пластины D : x =1, y =0, y = x, если поверхностная плотность в каждой ее точке µ(x, y)= x2 + 2y2 +10.

3.Найти статический момент однородной пластины D : x2 + y2 + 2x =0,

x2 + y2 + x =0, y ≥0, относительно оси Oy , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область V :
x = 2 y2 + z2 , y2 + z2 = 4, x =0.
5.	Найти момент инерции однородного тела относительно оси Oz , занимающего

область V : 2z = x2 + y2 , z = 2.

6.Найти объем тела, ограниченного поверхностями: z =9 − x2 − y2 , z =0,

x2 + y2 ≥ 4.

7.Вычислить непосредственно и с помощью формулы Грина:

∫2(x2 + y2 )dx +(x + y)2 dy , где L − контур треугольника ABC : A(2;1), B(4;1),

L

C(4;2).

8.Вычислите поток векторного поля F = xi + yj + zk через внешнюю сторону границы области, ограниченной поверхностями x + y2 =1, x =0, z = 2 и z =0 .

9.Вычислить модуль криволинейного интеграла (циркуляцию)

3

x

z

2

x

2

y

2

∫

y

+

−2y

dx +

2x +

dy +(z2 + xz)dz , где C − линия пересечения

C

3

2

2

эллипсоида

3x

2

+

y2

+ z2

=1 с плоскостью x = 2z .

4

9

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a = x2 (−xi +3zk ).

Вариант 19

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области D : x = −1, x = −2, y ≥0,

D

y = x2 .

2.Найти массу неоднородной пластины D : y =0, y = 2x, x + y =6, если поверхностная плотность в каждой ее точке µ(x, y)= x2.

3.Найти статический момент однородной пластины D : x2 + y2 −2x =0,

x2 + y2 − x =0, y ≤0, относительно оси Ox , используя полярные координаты.

4.	Найти координаты центра масс однородного тела, занимающего область V :
4y = x2 + z2 , y =9.
5.	Найти момент инерции однородного тела относительно оси	Ox , занимающего
область V : x2 = y2 + z2 , y2 + z2 = 4, x =0.
6.	Найти объем тела, ограниченного поверхностями: z = 4 − x2 ,	y =0, z = y.
7.	Вычислить непосредственно и с помощью формулы Грина:
∫	(x + y)2 dx +(x − y)2 dy, где L : y = x2 ,
L	y = x.

8.Вычислите поток векторного поля F = xyi + yzj + zk через внешнюю сторону границы области, ограниченной поверхностями x + z =1, x − y =0, y =0 и z =0 .

9.Найдите циркуляцию векторного поля F =(xz + y)i + yzj + 2xyk по контуру,

вырезанному из двуполостного гиперболоида x2 + y2 − z2 +16 =0 плоскостями x =0, y =0 и z =5 при x ≥0, y ≥0.

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a =ex (−yj + zk ).

Вариант 20

1. Расставить пределы интегрирования двумя способами в двойном интеграле ∫∫ f (x, y)dxdy в декартовых координатах для области D : y ≤0, x2 = −y,

D

x = 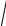2 − y2 .

2.	Найти массу неоднородной пластины D : x ≥0, y ≥0, x2 + y2 = 4,если
поверхностная плотность в каждой ее точке µ(x, y)= 4 − x2.
3.	Найти статический момент однородной пластины D : x2 + y2 + 2x =0,
x2 + y2 + x =0, y ≤0, относительно оси Oy , используя полярные координаты.
4.	Найти координаты центра масс однородного тела, занимающего область V :
x =5 y2 + z2 , x = 20.
5.	Найти момент инерции однородного тела относительно оси Oz , занимающего

область V : 2z = x2 + y2 , x2 + y2 = 4, z =0.

6.Найти объем тела, ограниченного поверхностями: x2 + y2 − z2 = 4, x2 + y2 =9.

7.Вычислить непосредственно и с помощью формулы Грина:

∫2(x + y)dx −(x − y)dy , где L −часть параболы y = x2 и хорда, проходящая через

L

точки A(−1;1), B(1;1).

8. Вычислите поток векторного поля F = x3i − y3 j + xz3k через внешнюю сторону границы области, ограниченной поверхностями x2 + y2 =9 и x2 + y2 + z2 = 25

( x2 + y2 ≤9).

9. Вычислить криволинейный интеграл (циркуляцию)

∫(y + z)dx +(2x − z)dy +(y +3z)dz , где C −контур треугольника с вершинами

C

A(3;0;0), B(0;3;0), C (0;0;3) , который обходится в направлении ABCA.

10. Найти дивергенцию и ротор векторного поля a ; выяснить, является ли данное поле потенциальным или соленоидальным; если да, то найти соответственно его скалярный или векторный потенциал и сделать проверку потенциала:

a =(−x − y)i + zk.