
- •Санкт-Петербургский университет управления и экономики
- •2014 Оглавление
- •Требования к оформлению контрольных работ
- •Формирование исходных данных к задачам
- •Рекомендуемая литература
- •Краткие теоретические сведения для выполнения контрольной работы № 1 и решение типовых задач
- •1.1. Матрицы и действия над ними
- •Действия над матрицами
- •1.2. Определители 2-го и 3-го порядков
- •Вычисление определителей 2-го и 3-го порядка
- •Свойства определителей
- •1.3. Обратная матрица
- •1.4. Решение систем линейных алгебраических уравнений (слаУр)
- •Формулы Крамера для решения слаУр
- •Рассмотрим матрицу специального вида
- •Метод Гаусса решения слаУр
- •Краткие теоретические сведения для выполнения контрольной работы № 2 и решение типовых задач
- •2.1. Прямая на плоскости
- •Условие параллельности двух прямых
- •Условие перпендикулярности двух прямых
- •2.2. Элементы векторной алгебры и аналитической геометрии в пространстве
- •Краткие теоретические сведения для выполнения контрольной работы № 3 и решение типовых задач
- •3.1. Раскрытие неопределенности вида .
- •3.2. Раскрытие неопределенности вида
- •3.3. Вычисление пределов с использованием второго замечательного предела
- •3.4. Непрерывность функции
- •Классификация точек разрыва
- •3.5. Правила дифференцирования
- •Правила дифференцирования
- •3.6. Производная сложной функции
- •3.7. Метод логарифмического дифференцирования
- •3.8. Производная функции, заданной неявно
- •3.9. Дифференцирование функций, заданных параметрически
- •3.10. Исследование функций и построение графиков функций
- •Краткие теоретические сведения для выполнения контрольной работы № 4 и решение типовых задач
- •4.1. Метод интегрирования подведением под знак дифференциала
- •4.2. Метод интегрирования по частям
- •4.3. Интегрирование тригонометрических выражений
- •4.4. Вычисление площадей с помощью определенного интеграла
- •1. Элементы линейной алгебры
- •2. Элементы векторной алгебры и аналитической геометрии
- •3. Предел и производная функции одной переменной
- •4. Интегральное исчисление функции одной переменной
1.3. Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей
по отношению к данной А
называется матрица
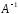 ,
которая будучи умноженной, как справа,
так и слева на данную матрицу, дает
единичную матрицу.
,
которая будучи умноженной, как справа,
так и слева на данную матрицу, дает
единичную матрицу.
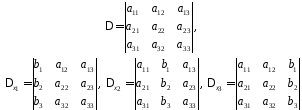
По определению
А
·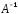 =
=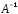 · А = Е.
· А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
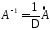 ,
,
где
 - определитель матрицыА,
- определитель матрицыА,
 - союзная матрица по отношению к данной
матрице, в которой элементы каждой
строки данной матрицы заменены
алгебраическими дополнениями элементов
соответствующих столбцов. Например,
для квадратной матрицы 2-го порядка
союзной является матрица
- союзная матрица по отношению к данной
матрице, в которой элементы каждой
строки данной матрицы заменены
алгебраическими дополнениями элементов
соответствующих столбцов. Например,
для квадратной матрицы 2-го порядка
союзной является матрица
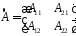 ,
,
для квадратной матрицы 3-го порядка союзной является матрица
 .
.
Пример
Для матрицы
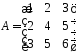 найти обратную.
найти обратную.
Решение
Обратную матрицу находим по формуле
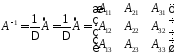 .
.
Определитель
матрицы
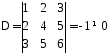 ,
следовательно, матрица неособенная и
обратная матрица существует. Найдем
алгебраические дополнения элементов
матрицы:
,
следовательно, матрица неособенная и
обратная матрица существует. Найдем
алгебраические дополнения элементов
матрицы:
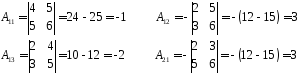
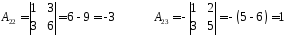
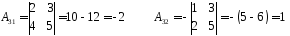
 .
.
Тогда обратная матрица имеет вид
 .
.
1.4. Решение систем линейных алгебраических уравнений (слаУр)
Рассмотрим систему трех линейных уравнений с тремя неизвестными:
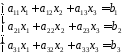 .
(1)
.
(1)
Если хотя бы одно
из чисел
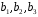 не равно нулю, то такая система называетсянеоднородной.
Если же
не равно нулю, то такая система называетсянеоднородной.
Если же
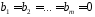 ,
то такая система называетсяоднородной.
,
то такая система называетсяоднородной.
Решением
системы (1) называется упорядоченная
совокупность чисел
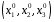 ,
которая при подстановке в систему
обращает все уравнения системы в верные
равенства.
,
которая при подстановке в систему
обращает все уравнения системы в верные
равенства.
Если система имеет решение, то она называется совместной, если не имеет решения – то несовместной. Если система имеет единственное решение, то она называется определенной, если более одного решения, то – неопределенной.
Формулы Крамера для решения слаУр
Если
определитель системы
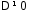 ,
то эта система имеет единственное
решение, которое можно получить по
формулам Крамера.
Формулы
Крамера
имеют вид
,
то эта система имеет единственное
решение, которое можно получить по
формулам Крамера.
Формулы
Крамера
имеют вид
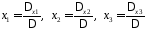 ,
,
где
 .
.
В
знаменателях этих формул стоит
определитель системы
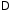 ,
а в числителях – определители, которые
получаются из определителя системы
,
а в числителях – определители, которые
получаются из определителя системы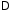 заменой коэффициентов при соответствующих
неизвестных столбцом свободных членов.
заменой коэффициентов при соответствующих
неизвестных столбцом свободных членов.
Пример 1.
Решить
систему
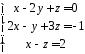 по формулам Крамера.
по формулам Крамера.
Решение
Формулы
Крамера:
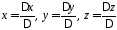 .
Вычислим определители:
.
Вычислим определители:
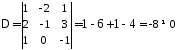 ,
,
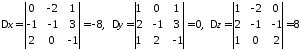 ,
тогда
,
тогда
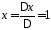 ,
,
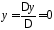 ,
,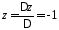 .
.
Итак,
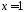 ,
,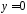 ,
,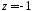 .
.
Ранг матрицы
Пусть дана матрица
 .
.
Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров. Обозначение: rang A, r(А) или r.
Очевидно,
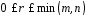 – меньшее из чиселm
и n.
– меньшее из чиселm
и n.
Минор, порядок которого определяет ранг матрицы, называется базисным. Вычисление всех миноров отличных от нуля трудоемкая операция. На практике для вычисления r(A) используют метод Гаусса.
Элементарными преобразованиями называются следующие действия над матрицами:
Вычеркивание нулевой строки.
Умножение какой либо строки на число.
Прибавление к одной из строк другой строки, умноженной на любое число.
Перестановка двух столбцов или двух строк.
Теорема 1. Ранг матрицы не меняется при элементарных преобразованиях.
