МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Забайкальский государственный университет»

(ФГБОУ ВПО «ЗабГУ»)

Энергетический факультет

Кафедра информатики и вычислительной техники

Отчет №3

по дисциплине: «Алгоритмы обработки данных»

Выполнил ст. гр. ИВТ-13-2(ВМК)

(группа)

Забелин В.О.

(фамилия, инициалы)

Чита

2015

1.Деревья

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Условия: является связанным графом, не содержащим циклы, рёбра графа не должны быть ориентированными, рёбра графа не должны быть взвешенными.

Данные, имеющие иерархическую структуру, удобно представлять с помощью деревьев. Дерево представляет собой конечное множество элементов, называемых узлами, или вершинами. Вершины расположены на разных уровнях иерархии. На самом высоком уровне иерархии (пусть номер этого уровня 1) располагается единственный узел, называемый корнем. Каждый узел, расположенный на i-ом уровне, связан на более высоком (i1)-ом уровне с единственным узлом, который является исходным, или предком для данного узла. Каждый узел i-ого уровня может быть связан с одним или несколькими узлами на более низком (i+1)-ом уровне. Такие узлы (i+1)-ого уровня называются порожденными узлами, или потомками. Узлы, не имеющие порожденных, называются листьями. На плоскости узлы удобно изображать точками, узлы i-ого уровня связывать дугами с порожденными узлами (i+1)-ого уровня. Примером дерева может служить генеалогическое дерево, в котором порожденными узлами являются сыновья. На рисунке 1 изображено лишь два поколения потомков Александра Невского: сыновья и внуки.

Можно построить генеалогическое дерево своей семьи, выбрав в качестве корня дерева, например, прадедушку. С помощью дерева можно представить родословную некоторого человека. В таком дереве каждый узел имеет два порожденных, например, левый узел хранит данные о матери, правый об отце. На каком-то уровне информация о родственниках безвозвратно утеряна.

Очень часто при решении задачи перед программистом возникает проблема выбора наиболее подходящей структуры данных, но чтобы сделать правильный выбор необходимо знать сильные и слабые стороны этих структур.

В различных задачах применяются различные виды деревьев, так например:

• при разработке парсеров или трансляторов полезным может оказаться дерево синтаксического разбора (синтаксическое дерево) [ 5 ];

• при работе со строками удобными могут оказаться суффиксные деревья;

• при разработке оптимальных алгоритмов на графах полезным может оказаться структура данных в виде кучи;

• двоичные деревья поиска используются при реализациях словаря, они являются достаточно простым и распространенным видом деревьев, поэтому их мы рассмотрим более подробно;

• перечислять дальше виды деревьев не имеет смысла, думаю, уже понятно, что разновидностей деревьев много, и у каждой есть своя сфера применения.

Двоичное дерево поиска — это двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

• Оба поддерева — левое и правое — являются двоичными деревьями поиска.

• У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.

• В то время, как значения ключей данных у всех узлов правого поддерева (того же узла X) больше, нежели значение ключа данных узла X.

Очевидно, данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.

Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако это касается реализации, а не природы двоичного дерева поиска.

Для целей реализации двоичное дерево поиска можно определить так:

• Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные, привязанные к узлу, left и right — ссылки на узлы, являющиеся детьми данного узла — левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также определения поля parent в каждом узле (кроме корневого) — ссылки на родительский элемент.

• Данные (data) обладают ключом (key), на котором определена операция сравнения «меньше». В конкретных реализациях это может быть пара (key, value) — (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неё.

• Для любого узла X выполняются свойства дерева поиска: key[left[X]] < key[X] ≤ key[right[X]], то есть ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Двоичное дерево поиска не следует путать с двоичной кучей, построенной по другим правилам.

Основным преимуществом двоичного дерева поиска перед другими структурами данных является возможная высокая эффективность реализации основанных на нём алгоритмов поиска и сортировки.

Двоичное дерево поиска применяется для построения более абстрактных структур, таких, как множества, мультимножества, ассоциативные массивы.

Особенность дерева поиска заключается в том, значения вершин левого поддерева меньше или равны значению корневого узла, а правого – больше (порядок может быть изменен на противоположный).

При обходе дерева поиска, начиная с левого поддерева, значения будут просмотрены в порядке неубывания, начиная с правого – невозрастания, т.е. дерево поиска хранит отсортированные данные.

Преимущества деревьев нельзя описать отдельно, любые преимущества существуют относительно чего-либо. Дальше очень коротко деревья поиска сравниваются с динамическими списками и массивами (отсортированными и неотсортированными).

Известно, что операция поиска элемента в неотсортированном массиве имеет сложность O(n), а в отсортированном – O(log(n)), n – количество элементов в дереве/списке. Логарифмическая сложность поиска в отсортированном массиве обеспечивается двоичным поиском, т.е. вместо того, чтобы обходить все элементы массива последовательно, массив каждый раз делится пополам, поиск продолжается в половине массива (очень похоже на поиск по оглавлению книги или поиск слова в обычном, бумажном словаре). Поиск элементов в отсортированном массиве выполняется очень быстро, однако, вставка элемента в отсортированный массив потребует сдвига элементов (операция со сложностью O(n)).

Операция вставки элемента в отсортированный динамический список не требует сдвига элементов, однако, перед тем как вставить элемент, необходимо найти подходящую позицию. Для связных списков нельзя использовать двоичный поиск (т.к. элементы могут располагаться в памяти не последовательно друг за другом), а значит, что операция вставки и поиска элемента отсортированном динамическом списке имеет сложность O(n).

Таким образом, поиск в отсортированном массиве имеет логарифмическую сложность, однако, операция вставки имеет сложность O(n), динамические списки не решают проблему.

Деревья поиска позволяют выполнять операцию вставки элемента за время O(log(n)), а операцию поиска – за O(h), где h – высота дерева. В примерах следующего раздела будет приведен пример правила построения произвольного дерева поиска (не сбалансированного), высота которого в худшем случае совпадает с количеством элементов в дереве (так будет если в дерево добавлять уже отсортированные данные), однако, обычно и такое дерево будет иметь высоту весьма близкую к log(n). Высота сбалансированного дерева поиска – log(n), поиск всбалансированном дереве поиска (это такое дерево, высота правого и левого поддерева, которого различаются не более чем на единицу) выполнится за время O(log(n)). Отмечу, что существуют самобалансирующиеся деревья поиска, например, красно-черные деревья, АВЛ-деревья или расширяющиеся деревья, но их рассмотрение выходит за рамки статьи [2, 5, 6].

Конечно, дерево поиска необходимо поддерживать в отсортированном состоянии, операции добавления или удаления элементов выполняются дольше, чем в неотсортированных массивах или списках.

Добавление элемента (E) в дерево поиска выполняется рекурсивно:

если дерево является пустым – то значение E помещается в корневую вершину;

если значение E больше значения корневой вершины – осуществляется вставка Eв правое поддерево (рекурсивно), иначе – в левое.

Удаление элемента (E) из дерева поиска, несколько запутаннее, поэтому алгоритм тут не приведен, зато приведены поясняющие иллюстрации (рисунок 1).

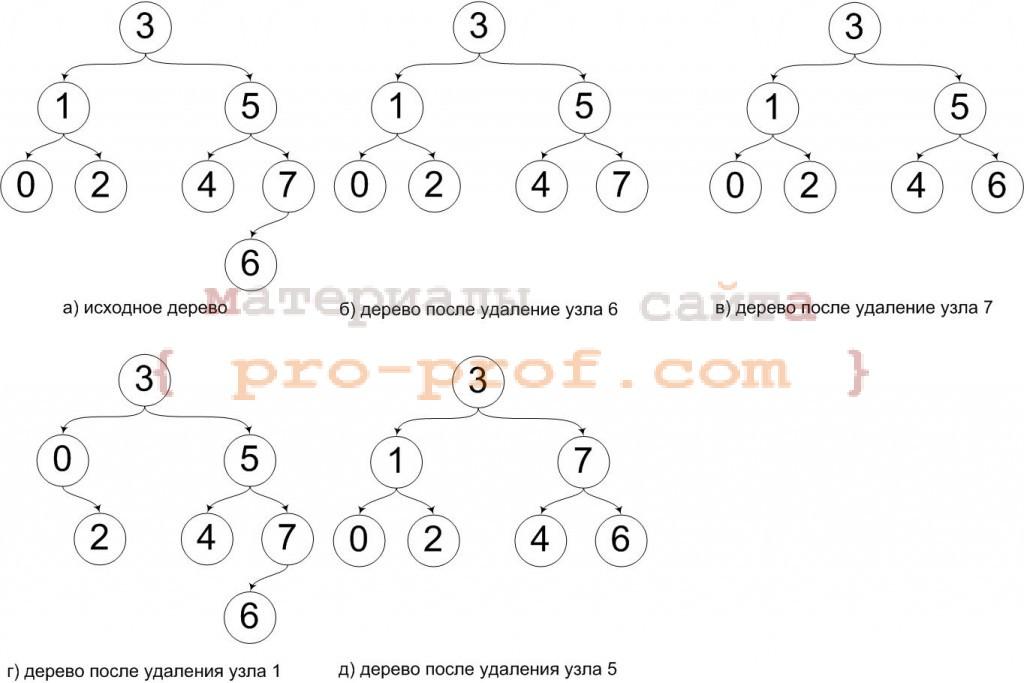
рис. 1 удаление узла из дерева поиска

На рисунке видно, что удаление листа (рис 1.б) сложности не представляет, ровно как и удаление узла, имеющего лишь одного потомка (рис 1.в). В остальных случаях (рис. 1.г, 1.д) необходимо учитывать в каком поддереве (левом или правом) расположен удаляемый узел.

Такие алгоритмы добавления элемента и удаления элемента дерева имеют трудоемкость O(log(n)), однако не гарантируют сбалансированности полученного дерева. Аналогичные операции для, например, красно-черных деревьев сложнее, но их трудоемкость, по-прежнему, O(log(n)).

Нередко пишут, что деревья сложнее в использовании, чем массивы и списки, на самом деле, это не всегда так и зависит от используемых библиотек. Например, контейнер словаря (map) стандартной библиотеки С++ чаще всего реализуется через красно-черные деревья, но нельзя сказать, что он менее удобен в использовании чем список (list) из той же библиотеки – каждый из них имеет свою область применения и удобен тогда, когда используется по назначению.