1. Вещественные и комплексные числа

1.1. Множества. Обозначения. Логические символы

Понятие множества является одним из основных в математике. Слова «совокупность», «семейство», «система», «набор» и т. д. – синонимы слова «множество». Множество может содержать конечное (количество студентов в аудитории) или бесконечное (количество точек на прямой) число произвольных объектов.

Определение. Объекты, из которых состоит множество, называются его элементами, или точками.

Множества часто обозначают большими буквами, а его элементы – маленькими. Если – элемент множества, то пишут, в противном случае ─. Если - некоторые элементы множества , то запись означает, что множество состоит из элементов .

Пусть даны два множества и. Еслиисостоят из одних и тех же элементов, то говорят, что эти множества совпадают, и пишут. Если внет элементов, не принадлежащих, тосодержится в(– подмножество множества). В этом случае пишут, или(содержит). Еслине содержится в, то пишут.

В математике часто используется пустое множество. Оно не содержит ни одного элемента и обозначается символом . Пустое множество является подмножеством любого множества.

В математических предложениях повторяются отдельные слова и целые выражения. Поэтому для их записи используется логическая символика.

Рассмотрим несколько самых простых и наиболее употребляемых логических символов. Вместо слова «существует» или «найдется» используют символ  (перевернутая латинская буква Е от английского слова Existence – «существование»), а вместо слов «любой», «каждый», «всякий» ─ символ  (перевернутое латинское А от английского слова Any ─ любой).

Например, запись означает, что «существует элемент из множества…». Запись означает: «для любого найдется, зависящее оти большее 0…».

Для облегчения понимания и чтения утверждений, записанных с помощью логических символов, все, что относится только к каждому из них, заключается в круглые скобки. Например, запись

читается так: «для любого существует такое, что для всех , не равных и удовлетворяющих неравенству , выполняется неравенство .

1.2. Вещественные числа и их основные свойства

Известно, что множество вещественных чисел состоит из множества рациональных и множества иррациональных чисел.

Определение. Рациональным называется число, которое можно представить в виде p/q, где p и q – целые числа, причем q  0.

Определение. Всякое вещественное число, которое не является рациональным, называется иррациональным.

Любое рациональное число является либо целым, либо представляется конечной или периодической бесконечной десятичной дробью (;). Иррациональное число представляется непериодической бесконечной десятичной дробью (; = 3,14159…).

Основные свойства вещественных чисел

Сложение и умножение вещественных чисел. Для любой пары a и b вещественных чисел определены единственным образом два вещественных числа a+b и a·b, называемые соответственно их суммой и произведением. Для любых вещественных чисел a, b, c выполняются следующие свойства:

1. a + b = b + a (переместительное свойство сложения);

2. a + (b + c) = (a + b) + c (сочетательное свойство сложения);

3. a · b = b · a (переместительное свойство умножения);

4. a · (b ·c) = (a · b) · c (сочетательное свойство умножения);

5. (a + b) · c = a · c + b · c (распределительное свойство);

6. существует единственное число 0 такое, что a + 0 = 0 + a = a для любого числа a;

7. для любого числа a существует число (- a) такое, что a + (- a) = 0;

8. существует единственное число 1  0 такое, что для любого числа a имеет место равенство a · 1 = a;

9. для любого числа a  0 существует такое число a^-1 , что a · a^-1 =1, число a^-1 обозначается также символом .

Сравнение вещественных чисел. Для любых двух вещественных чисел a и b установлено одно из соотношений: a = b (a равно b), a  b (a больше b) или a  b. Каковы бы ни были числа a, b, c, выполняются соотношения:

1. если a = b и b = с, то a = с;

2. если a  b и b  с, то a  с;

3. если a  b, то a + c  b + c;

4. если a  0, b  0, то a · b  0.

Непрерывность вещественных чисел. Пусть X и Y ─ два множества, состоящих из вещественных чисел. Тогда, если для любых чисел x X и yY выполняется неравенство x ≤ y, то существует хотя бы одно число с такое, что для всех таких x и y выполняются неравенства x ≤ с ≤ y.

Свойством непрерывности обладает множество всех вещественных чисел. Однако множество только рациональных чисел таким свойством не обладает.

Теорема. Множество рациональных чисел не является непрерывным.

Доказательство. Доказывать будем «методом от противного». Пусть , .Тогда для ,выполняется неравенство, поэтомутакое, что. Однако таким числом может быть только число, которое не является рациональным. Пришли к противоречию. Теорема доказана.

Рассмотрим еще несколько свойств вещественных чисел, которые вытекают из сказанного. Для любых вещественных чисел a, b, c, d:

1. Число x = b + (- a) является решением уравнения a + x = b.

Доказательство..

Определение. Число b + (- a) называется разностью чисел b и a и обозначается b – a.

2. Если b  a, то b – a  0.

Доказательство. ,тогда или .

3. Число x = b · a^-1 является решением уравнения a · x = b, если a  0.

Доказательство. .

Определение. Число b · a^-1 называется частным чисел b и a и обозначается , илиb : a.

4. Если a  b, то – a  - b.

Доказательство. Так как , то и , следовательно, .

5. Если a  b, c  d, то a + c  b + d.

Доказательство. , тогда . , следовательно,. Таким образом, .

6. Если a  b, c  d, то a – c b – d. Это свойство доказывается с использованием свойств 4 и 5.

7. a – a = 0.

Доказательство. .

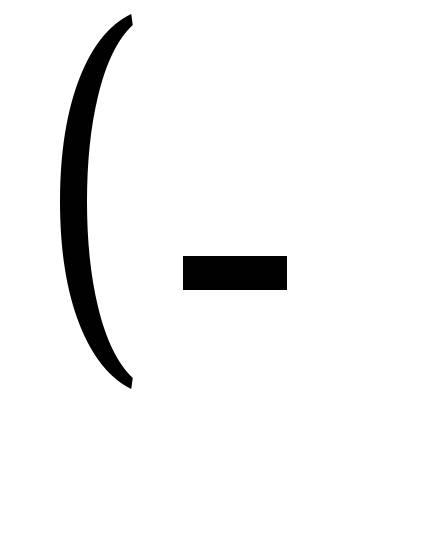8. – a) = a.

Доказательство. .

9. a · 0 = 0.

Доказательство..

10. (- a)b = - ab.

Доказательство..