Занятие 2(Фдз 3)
.doc
Занятие 2 (Фдз 3). Однородные и неоднородные системы линейных уравнений.
2.1. Однородная система линейных уравнений, ее совместность. Теорема о структуре общего решения линейной однородной системы. Базис (фундаментальная система решений) и размерность пространства решений линейной однородной системы.
2.2. Неоднородная система линейных уравнений, соответствующая ей однородная система. Теорема о структуре совместной линейной неоднородной системы.
2.1. Линейная система алгебраических уравнений называется однородной, если все ее свободные члены равны нулю. Т.е. линейная однородная система, это – система вида
.
Однородная система
всегда совместна, у нее есть тривиальное
решение:
.
Структуру общего решения линейной
однородной системы определяет следующая
теорема.
Множество всех решений линейной однородной системы образует линейное пространство.
Базис этого пространства решений называется фундаментальной системой решений (сокращенно ФСР).
Пример 1. Найти общее решение и ФСР однородной системы
.
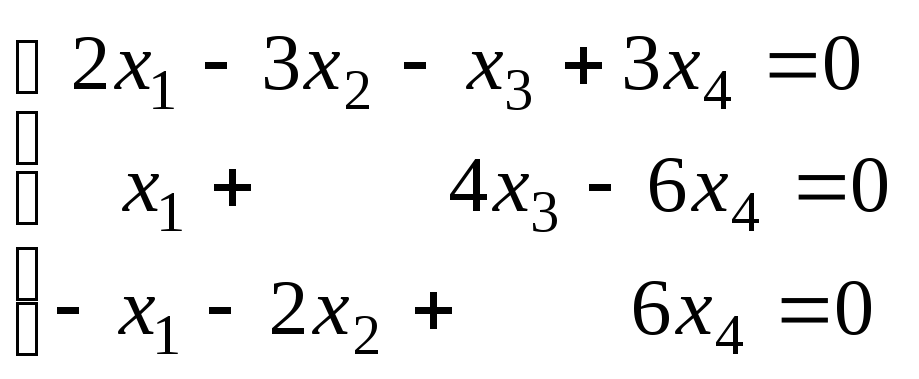(1)
Решение.
Применим метод
Гаусса. Преобразования системы проводим
на ее матрице
.
.
(2)
Здесь были выполнены следующие операции:
1) в матрице
переставили местами 1-ю и 2-ю строки
(получили матрицу
);
2) в матрице
прибавили ко 2-й строке 1-ю строку,
умноженную на число (-2) и
к 3-й строке
прибавили 1-ю строку (получили матрицу
);
3) в матрице
2-ю строку разделили на (-3) и
3-ю строку
разделили на 2 (получили матрицу
);
4) в матрице
к 3-й строке прибавили 2-ю строку (получили
матрицу
);
5) в матрице
3-ю строку разделили на 5 и получили
матрицу
треугольного вида.
По матрице
находим соответствующую однородную
систему (2), эквивалентную системе (1).
В системе (2)
неизвестная
является свободной, а неизвестные
- базисными.
Положим,
,
где
-
произвольное число. Затем, из 3-го, 2-го
и 1-го уравнений системы (2) последовательно
находим
,
,
.
Следовательно,
общее решение системы (1) можно записать
в виде
,
где
.
Перепишем это
решение в векторном виде
.
Отсюда видно, общее решение системы (1) является одномерным линейным пространством с базисом
.
Таким образом,
фундаментальная система решений системы
(1) состоит из одного решения
.
Пример 2. Найти общее решение и ФСР однородной системы
.
(3)
Решение.
Применим метод
Гаусса. Преобразования системы проводим
на ее матрице
.
.
(4)
Здесь были выполнены следующие операции:
1) в матрице
переставили местами 1-ю и 3-ю строки
(получили матрицу
);
2) в матрице
ко 2-й строке прибавили 1-ю строку,
умноженную на 2,
к 3-й строке
прибавили 1-ю строку, умноженную на (
)
и
к 4-й строке
прибавили 1-ю строку, умноженную на (
),
(получили матрицу
),
3) в матрице
к 3-й строке прибавили 2-ю строку и 4-й
строке прибавили 2-ю строку,
(получили матрицу
треугольного вида).
Матрице
соответствует однородная система (4),
эквивалентная системе (3).
У системы (4)
неизвестные
являются свободными, а неизвестные
-
базисными.
Положим,
,
где
-
произвольные числа. Затем, из 2-го и 1-го
уравнений системы (2) последовательно
находим
,
.
Таким образом,
общее решение системы (3) можно записать
в виде:
.
Это решение в
векторной форме перепишется так:
.
Отсюда видно, что множество всех решений является трехмерным линейным пространством, представленным линейной оболочкой на следующих трех решениях
.
Эти три решения - базис пространства решений системы (3), т.е. ее фундаментальная система решений (ФСР).
Пример 3. Найти общее решение и ФСР однородной системы
.
(5)
Решение.
Заданная система (5) является невырожденной системой, т.к. ее главный определитель
,
отличен от нуля. В силу правилу Крамера система (5) имеет только одно решение:
или в векторном
виде
.
В данном случае общее решение системы образует линейное пространство из одного нулевого элемента. Это пространство имеет нулевую размерность и не имеет базиса. Поэтому, ФСР у системы (5) нет.
2.2. Рассмотрим теперь линейную неоднородную систему алгебраических уравнений
.
(6)
Если все свободные члены системы (6) заменить нулями, то получающаяся однородная система
называется соответствующей однородной системой.
Если система (6) совместна (напомним, что для этого необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы), то ее общее решение подчиняется следующей теореме.
Теорема (о структуре общего решения неоднородной системы). Общее решение неоднородной системы состоит из общего решения соответствующей однородной системы плюс частное решение неоднородной системы.
При исследовании линейной неоднородной системы требуется уметь находить общее решение и выделять из него общее решение соответствующей однородной системы и частное решение неоднородной системы.
Пример 4. Найти общее решение неоднородной системы
(7)
и выделить их него: частное решение неоднородной системы и общее решение соответствующей однородной системы с указанием ее ФСР.
Решение. Применим
метод Гаусса. Преобразования заданной
системы осуществим с помощью расширенной
матрицы
системы.
Решение проведем с использованием расширенных матриц.
(8)
Здесь:
1) в матрице
переставили местами 1-ю и 3-ю строки
(получили матрицу
);
2) в матрице
ко 2-й строке прибавили 1-ю строку,
умноженную на 2,
к 3-й строке
прибавили 1-ю строку, умноженную на (
)
и
к 4-й строке
прибавили 1-ю строку, умноженную на (
),
(получили матрицу
);
3) в матрице
к 3-й строке прибавили 2-ю строку и 4-й
строке прибавили 2-ю строку
(получили матрицу
);
4) в матрице
отбросили несущественные нулевые строки
и 2-ю строку разделили на (-5),
(получили матрицу
треугольного вида).
Матрице
соответствует неоднородная система
(8), эквивалентная заданной неоднородной
системе (7).
У системы (8)
неизвестные
являются свободными, а неизвестные
-
базисными.
Положим,
,
где
-
произвольные числа. Затем, из 2-го и 1-го
уравнений системы (8) последовательно
находим
,
.
Таким образом,
общее решение системы (5) можно записать
в виде:
.
Это решение в
векторной форме перепишется так:
.
Если в найденном
решении положить
,
то получим частное решение неоднородной
системы (7)
.
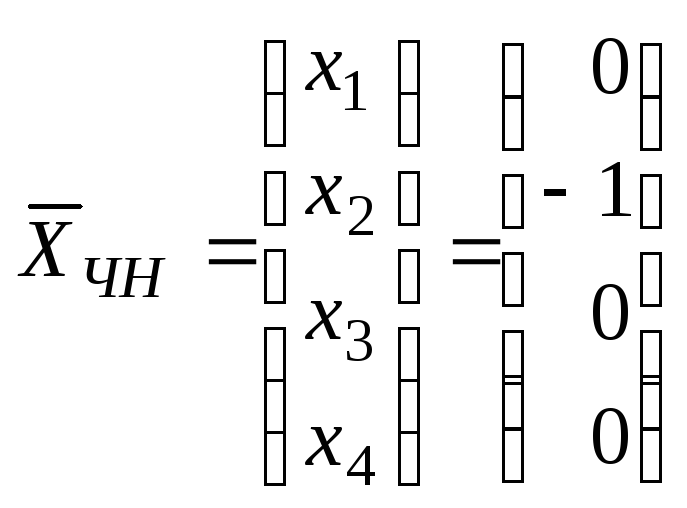Общее решение соответствующей однородной системы это
.
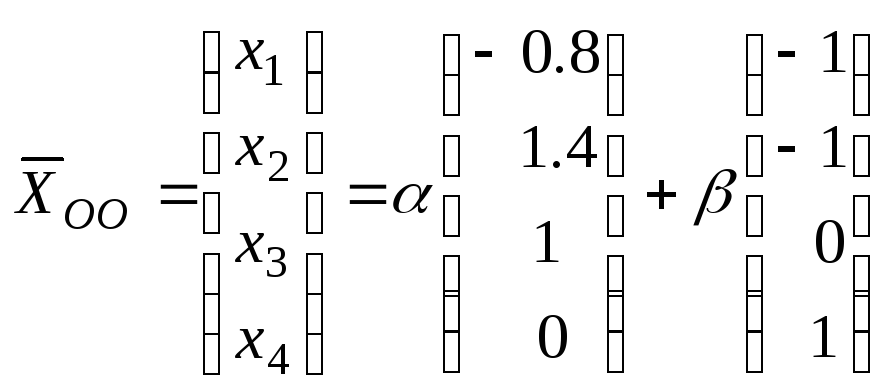ФСР общего решения соответствующей однородной системы представляют два решения
.
Пример 5. Найти общее решение неоднородной системы
(9)
и выделить их него: частное решение неоднородной системы и общее решение соответствующей однородной системы с указанием ее ФСР.
Решение.
Данная система является невырожденной и ее можно решить по правилу Крамера.
- главный определитель системы.
Вспомогательные определители:
,
,
.
.
Общее решение
системы состоит из одного решения
.
В векторном виде
это решение запишется так:
или
.
Частное решение
неоднородной системы (9):
.
Общее решение
соответствующей однородной системы:
.
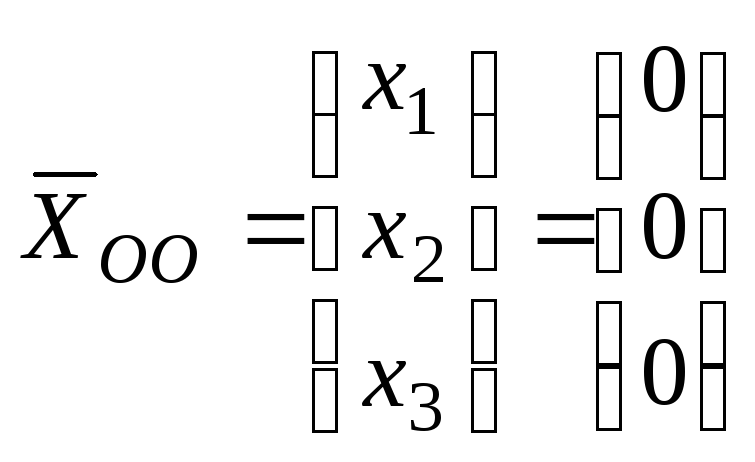образует линейное
пространство нулевой размерности.
Поэтому, фундаментальной системы
решений у
нет.
__________________________________________________________________________________
Домашнее задание.
1. Найти общее решение и фундаментальную систему решений у следующих однородных систем:
1.1.
;
1.2.
.
2. Найти общее решение неоднородной системы. Выделить из него частное решение этой системы и общее решение соответствующей однородной системы (с указанием ФСР).
.
3. Найти общее решение неоднородной системы. Выделить из него частное решение этой системы и общее решение соответствующей однородной системы (с указанием ФСР).
.