19

§4. Функция одной переменной 1. Понятие функции и способы ее задания

Пара чисел х и у называется упорядоченной, если указано, какое из этих чисел считается первым, а какое - вторым. (х;у) Определение4.1 Пусть Х и У – некоторые числовые множества. Функцией называется множество f упорядоченных пар чисел (х;у) таких, что х Х, уУ и каждое х входит в одну и только одну пару этого множества, а каждое у входит, по крайней мере, в одну пару. При этом говорят, что числу х поставлено в соответствие число у, и пишут у=f(x). Число у называется значение функции f в точке х. Переменную у называют зависимой переменной, а переменную х – независимой (аргументом), множество Х – областью определения (существования х) функции, а множество У – множеством значений функции.

Вместо термина «функция» употребляют еще равнозначный термин «отображение», а вместо записи y=f(x) пишут f: x у и говорят, что отображениеf отображает число х в число у, или число у является образом числа х при отображении f.

Пусть на некотором множестве Х определена функция f(x), тогда значение этой функции, соответствующее некоторому значению аргумента х_о, обозначается у_о=f(x_o). Для нахождения значения у по данному значению х Х надо произвести над этим значением х определенную систему операцийf. Таким образом, если функция задана, то можно определить множество ее значений У={y}.

Область определения функции (может состоять из одного или нескольких промежутков, из отдельных точек и других множеств. Множество ее значений (определяется законом соответствия.

y=f(x), =[a;b],[c;d]

т.е. аргумент х изменяется от a до b a х 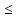b, а функция у изменяется от с до d (c y d)

Может оказаться, что область значения функции состоит из одного какого-нибудь числа С (геометрически из одной точки на оси Оу), т.е. каждому значению х, взятому из области определения функции, соответствует только одно число С. В этом случае функция постоянна f(x) = c = const

Способы задания функции

1. Аналитический

Этот способ состоит в том, что зависимость между переменными величинами определяется с помощью формулы, указывающей, какие действия можно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента. Примеры:

1. y=x³ + 7 задает функцию, область определения которой – числовая прямая (-; +) и такая же область значений;

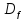2. у=задает функцию,= [-1; 1],

1-x²≥0 1-y²=x²

X=

3. y=n! = {1, 2, 3, … , n, …}= N,={1!, 2!, 3!, … , N!, …}

4. y = sgn x = = {-1, 0, 1}

[signum]

5. Функция Дирака у=

= {0, 1}

Эту функцию изобразить графически невозможно.

2. Табличный

x	0	0,1	0,2	3	0,6
y	-1	10	1	-2	-8

Поставим в соответствие каждому х, записанному в первой строке таблицы, число у, стоящее во второй строке под ними, числом х и будем говорить, что полученная функция задана таблицей. = {0; 0,1; 0,2; 3; 0,6],С помощью таблицы можно задать функцию только при конечном числе значений аргумента

3. Графический

Графиком функции у=f(x) называется множество точек плоскости, прямоугольные координаты которых удовлетворяют уравнению у=f(x). Функция у=f(x) называется заданной графически, если построен ее график. Такой способ задания функции дает возможность определить значения функции только приближенно, т.к. построение графика и нахождение на нем значений функции связано с погрешностями.

2. у=

4. y = sgn x =

2. Элементарные функции, их классификация

Функция у=f(x), заданная на множестве Х, называется элементарной, если ее можно задать одной формулой вида у=f(x) так, что ее значение элементарных операций («+», «-», «», «», возведение в степень, извлечение корня, логарифмирование, вычисление значений тригонометрических и обратных тригонометрических функций), причем число операций, сами операции и порядок их выполнения не зависит от значения аргумента х.

К классу элементарных функций относятся прежде всего все основные элементарные функции, а также функции, полученные из них при помощи конечного числа элементарных операций.

Например, элементарной функции y=lg(3x²-8) при х=6 равно2. Это значение найдено при помощи 4-х операций.

Примеры неэлементарных функций:

1. y=n! Количество операций, необходимое для определения значений 1-й функции, неограниченно возрастает с увеличением n.

2. у=

Она определена на всей числовой прямой 2-мя формулами и не может быть задана одной формулой с ограниченным числом элементарных действий.

Таким образом, если функция неэлементарная, то число операций над аргументом, либо сами операции, либо то и другое изменяются в зависимости от изменения аргумента.

Имеет место следующая классификация элементарных функций.

1. Функция вида Р(х)=а_ох^m+a₁x^m-1+…+a_m-1x+a_m, где m, m; a₀, a₁,… , a_m – любые целые числа (а₀0) – коэффициенты

Называется рациональной функцией или алгебраическим многочленом степени m. Многочлен 1-й степени называется линейной функцией.

2. Функция, представляющая собой отношение 2-х целых рациональных функций

R(x)=, называется дробно-рациональной функцией

Совокупность целых рациональных и дробно-рациональных функций образует класс рациональных функций.

3. Функция, полученная с помощью конечного арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющиеся рациональной, называется иррациональной.

4. Всякая функция, не являющаяся рациональной или иррациональной, называется трансцендентной функцией, например f(x)=sin x + x

3. Виды функций

Монотонные функции

Функция f(x) называется возрастающей (убывающей) на некотором множестве Х, если для любой пары чисел х₁ и х₂, принадлежащих этому множеству х₁ < х₂ => f(х₁) < f(х₂) (f(х₁) > f(х₂)), т.е. большому значению аргумента соответствует большое значение функции. Для любых х₁ и х₂ х₁ < х₂ => f(х₁) f(х₂) (f(х₁) 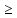f(х₂)) – неубывающая (невозрастающая)

Функция f(x) называется кусочно-монотонной на данном множестве, если это множество можно разбить на конечное число подмножеств, в каждом из которых функция изменяется монотонно.

Ограниченные функции

Функция y=f(x) называется ограниченной сверху (снизу) на некотором множестве Х, если существует такое число М (m), что f(x)≤ М (f(x) ≥ m) для любых х из этого множества. Функция называется ограниченной на некотором множестве Х, если она ограничена сверху и снизу, т.е. если существует М и m для любых x X m≤f(x)≤ М |f(x)| ≤ max {m,M}

Если таких чисел m и М не существует, то функция называется неограниченной

Пример:

=> на () функция кусочно-монотонная, ограничена снизу и ограничена сверху, т.е. -3<y<

Четные и нечетные функции

Функция называется четной (нечетной), если

1. симметрична относительно начала координат

2. 

График четной функции симметричен относительно оси Оу, нечетной – относительно начала координат.

Любую функцию f(x), заданную на симметричном относительно начала координат множестве, можно представить в виде суммы четной и нечетной функций на этом множестве. Это следует из того, что

f(x) =

Например, 5^х =

Периодические функции

Функция f(x) называется периодической, если существует такое число T>0, что для любого хпериод функцииf(x)

Отсюда следует, что , где с =const

Числа также являются периодами функции. Если число х=> числа (х+). Это значит, что если функция периодическая, то областью определения ее будет неограниченное множество действительных чисел, т.е. какое бы большое числоN>0 ни взяли, в найдется число |x+k|> N при достаточно больших k.

Наименьший положительный период функции f(x), если он существует, определяется минимальным периодом.

Если периодичная функция f(x) определена на всей числовой прямой, за исключением, может быть, изолированных точек, то для получения графика функции f(x) достаточно построить его в каком-либо сегменте [x₀, x₀+T]. Из сегмента удалены точки, где функция f(x) не определена, поэтому во всех сегментах [x₀+сТ, x₀+(с+1)T] графики функций f(x) в силу ее периодичности будут одинаковыми.

Например, y=tg x определена для любого xДля получения графика этой функции достаточно построить его на интервале (-

Сложная функция

Функция называется сложной, если ее аргумент в свою очередь является функцией другой переменной.

Если на некотором множестве Х определена функция z=со множеством значений, а на множестве- функция у=f(z), то функция у=f[] называется сложной функцией от х [суперпозицией функцийиf(z)], а переменная z – промежуточной переменной сложной функции.

Обратная функция

Пусть Х и У – некоторые множества и пусть задана функция f, т.е. множество пар чисел (х,у) (хХ, уУ), в котором любое число х входит в одну и только одну пару, а любое число у – по крайней мере в одну пару. Если в любой паре этого множества числа х и у поменять местами, то получим множество пар чисел (х;у), которое называется обратной функцией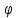к функцииf. Обратная функция х=(у).

Обратная функция не всегда является функцией, т.к. каждое число у может входить не только в одну, но и в несколько пар. Например, для функции y=x обратная функция х=у однозначна (любое число у входит в одну пару), для функции y=x² обратная функция х=двузначна (любое число у входит в 2 пары), а обратная функция х=arcsin y для функции y=sin x многозначна, т.к. любое число у входит в бесконечное число пар.

Из определения следует, что если обратная функция однозначна, т.е является функцией в обычном смысле, то множество значений У функции f служит областью определения обратной функции . Пусть, например, функцияy=f(x) определена на [a;b], и любоесоответствует ровно одномуx [a;b], тогда по определению на определена однозначная обратная функция х=(у),=[a;b].

Таким образом, функция y=f(x) и обратная функция х=(у) имеют один и тот же график, например, у=5 х и х=у. Если оси Ох и Оу поменять местами, для чего следует повернуть в пространстве плоскость Оху вокруг своей биссектрисыI координатного угла на 180⁰, то любое положение графика обратной функции х=(у) является графиком функции у=(х).

Теорема 4.1 (существование обратной функции)

Если функция y=f(x) возрастает (убывает) на множестве Х={х}, то на соответствующем множестве У={y} существует однозначная обратная функция х=(у), также возрастающая (убывающая).