ртцис

11

	s(t)
δ(t)
0	t

		s(t)
		δ(t-t0)
0	t0	t

Рисунок 1.2 − Фильтрующее свойство δ – функции и перенос действия из начала координат в точку t0

б)	Фильтрующее свойство δ – функции.
Использование δ		– функции позволяет аналитическим путем опреде-
лить значение сигнала в произвольной точке t0 :
	t2
	∫s(t) δ(t)dt =s(0),t1 < 0 < t2 ,					(1.4)
	t1
	t2
	∫s(t) δ(t −t0 )dt =s(t0 ), t1 < t0 < t2 .					(1.5)
	t1
в)	Дифференцирование δ – функции.
Применяя δ – функцию, можно оценить скорость изменения сигнала в
точке t0 :		′	≠ t0 ,			(1.6)
		δ (t −t0 ) = 0, t
	t2	t2
	∫s(t) δ′(t −t0 )dt =− ∫s′(t) δ(t −t0 )dt =− s′(t0 ) .					(1.7)
	t1	t1
г)	Интегрирование δ – функции.
Интегрирование δ – функции приводит к возникновению функции Хе-
висайда σ(t) :
	t	1,t > 0,
			1
	∫δ(τ)dτ =σ(t) =			2	,t = 0,	(1.8)
	−∞
		0,t < 0.

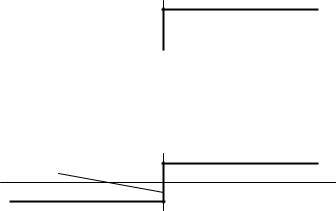
На функции Хевисайда (единичном скачке) остановимся подробнее. Единичный скачок не является функцией в смысле классического анализа.

Определяют функцию Хевисайда σ(t) как предел интеграла от дельта-

образующих семейств. Два семейства, переходящие в пределе к функции Хевисайда, изображены на рисунке 1.3.

12

Таблица 1.1. Дельта-образующие функции

Аналитическое выражение

Графическое представление

1

,

t

≤

τ

1

τ

δ(t) = lim τ

2

τ→0

t

τ

> 2

0,

τ

2

α

α 2

δ (t ) = lim

e

−α

t

2

α → ∞

t

δ ( t ) =

lim

α e −αt , t ≥ 0

α

α → ∞

t

δ(t) =

lim

sinωt

ω π

ω→∞

πt

1

ω

δ (t) =

lim

∫e jΩt dΩ

t

π

2ω

ω →∞ 2π

−ω

απ

1απ

δ (ω) = lim

α→0 α2 +ω2

ω

δ(ω) = lim

sin ω t

t

π

π ω

t→∞

1

t

δ (ω) = lim

∫e− jωτ dτ

π 2

ω

t →∞ 2π

−t

t

t

sinωτ

σ(t) = ∫δ(τ)dτ = ωlim→∞

∫

dτ

πτ

−∞

−∞

t

13

1
0	t

1
0	t

Рисунок 1.3 − Образование функций Хевисайда

Функцию Хевисайда изображают единичной ступенькой (с перебросом уровня в начале координат) и, видимо, поэтому называют функцией включения или единичным скачком.

Основные свойства функции Хевисайда: 1) аналитическая связь с δ – функцией

σ ′(t) = δ (t) ,	(1.9)

2) формирование одностороннего сигнала s(t) из произвольной функции f (t)

	f (t),t ≥ 0,	(1.10)
s(t) = f (t) σ(t) =
	0,t < 0,
3) определение значения сигнала в произвольной точке
∞
∫s(t) σ′(t − t0 )dt = s(t0 ) ,		(1.11)
−∞
4) определение скорости изменения сигнала в точке
∞	∞
∫s(t ) σ ′′(t − t0 )dt	= ∫s(t ) δ ′(t − t0 )dt = −s′(t0 ) .	(1.12)
−∞	−∞

Единичный скачок можно представить суммой четной и нечетной составляющих (рисунок 1.4):

σ (t) =	1	+	1	sign (t) .	(1.13)
	2		2

В таблице 1.1 представлены различные дельта - образующие функции с единичной площадью, которые при выполнении предельного перехода приобретают свойства δ – функции. Используется δ – функция в подынтегральных выражениях для сокращения объема преобразований и обеспечения

14

ясности при дифференцировании не только непрерывных, но и разрывных функций.

1 σ(t)

0,5			0		t
			0		t

0,5sign(t)	0,5
	0	t
	-0,5

Рисунок 1.4 − Графическое представление единичного скачка

1.2Описание алгоритмов взаимодействия обобщенных функций и сигналов

Функцию Хевисайда и δ – функцию можно сдвигать, перемножать с другими функциями, интегрировать (например, по частям), дифференцировать и т.д. Соответствующий математический аппарат разработан.

Функция Хевисайда и δ – функция - это линейные операторы (или функционалы), которые работают по определенным правилам, сведенным в таблицу 1.2. Правила эти просты и удобны. Они заменяют большой объем классических математических преобразований. Физический смысл преобразований с помощью обобщенных функций будем выяснять в процессе ознакомления с дисциплиной. Единичный скачок и δ – функция – это не только функционалы, предписывающие правила преобразований, они имеют самостоятельное применение в качестве «испытательных» сигналов в теории цепей.

Рассмотрим различные преобразования, позволяющие аналитическим путем осуществить выбор момента времени и определить значения сигнала в произвольной точке:

∞
∫s(t) δ(t −t0 ) dt = s(t0 ) ;	(1.14)

−∞

15
∞
∫s(t)σ′(t −t0 )dt =s(t0 ) ;	(1.15)
−∞
∞
∫s′(t)σ(t −t0 )dt = −s(t0 ) .	(1.16)

−∞

Реализации преобразований в виде структурных схем содержат специализированные блоки, выполняющие следующие операции:

- умножение; - задержка во времени;

∑- сложение;

	d	- дифференцирование во времени;
	dt

∫	- интегрирование во времени;

A - усиление (с коэффициэнтом усиления A);

-A - усиление (с коэффициэнтом усиления A и инверсией).

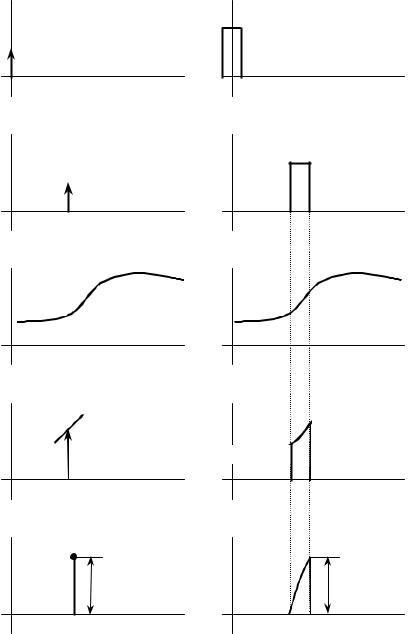
Структурная схема, соответствующая преобразованию (1.14), и временные диаграммы, поясняющие ее работу в отмеченных точках, изображены на рисунках 1.5 и 1.6.

1	2
	t0
δ(t)	δ(t-t0)

s(t)

4	∫	5
δ(t-t0)s(t)		s(t0)

3

Рисунок 1.5 − Реализация функционального преобразования (1.14)

			16
s1(t)			s1(t)
				rect(t)
	δ(t)
0		t	0		t
s2(t)			s2(t)
	δ(t-t0)				rect(t-t0)
0	t0	t	0	t0	t
s3(t)	s(t)		s3(t)		s(t)
0		t	0		t
s4(t)			s4(t)		s(t) rect(t-t0)
	s(t0) δ(t-t0)
0	t0	t	0	t0	t
s5(t)			s5(t)
	s(t0)				s(t0), t ≥ t0+τ/2
0	t0	t	0	t0	t

а) б)

Рисунок 1.6 − Временные диаграммы (эпюры напряжений в контрольных точках схемы рис. 1.5), поясняющие аналитический выбор значения сигнала в произвольный момент времени с помощью двух «испытательных» функций: а) δ –функции и б) прямоугольного импульса конечной длительно-

сти rect(t)

Структурные схемы, реализующие два способа определения значения сигнала в произвольный момент времени (1.15) и (1.16), представлены на рисунке 1.7.

17

σ(t)	d	σ′(t)	σ′(t-t0)
			t0
	dt

s(t0)

∫

s(t)

σ(t)

t0

σ(t-t0)

σ (t-t0) s′(t)

∫	-s(t0)	-1	s(t0)

s′(t)

s(t)	d
	dt

Рисунок 1.7 − Модификации структурных схем, соответствующие преобразованиям (1.15) и (1.16)

Путем аналогичных операций определяется скорость изменения сигнала в произвольной точке. Возможны различные формы записи интеграла взаимодействия сигнала и δ – функции с целью определения скорости:

∞
∫s′(t) δ(t −t0 ) dt = s′(t0 ) ;		(1.17)
−∞
∞	∞
∫s(t)δ′(t −t0 )dt = −	∫s′(t)δ(t −t0 )dt − s′(t0 ) .	(1.18)
−∞	−∞

Структурные схемы, формально реализующие необходимые линейные операции, изображены на рисунке 1.8

δ(t)	d
	dt

а)

δ′(t)	t0	δ′(t-t0)	δ′(t-t0) s(t)	∫	-s′(t0)	-1	s′(t0)

s(t)

δ(t)	t0	δ(t-t0)	δ (t-t0) s′(t)	∫	s′(t0)

б)

s′(t)

s(t)	d
	dt

Рисунок 1.8 − Два способа определения скорости изменения сигнала в точке t0: а) с инверсией и б) без инверсии

Таблица 1.2 – Правила взаимодействия обобщенных функций с сигналами

№

Описание преобразования

Математическое описание преобразования δ -функции

п/п

δ

∞, t = 0,

Определение δ – функции и

(t ) =

1

единичного

0, t ≠ 0.

скачка

t

1, t

> 0,

σ

(t ) = ∫ δ (t )dt =

< 0.

−∞

0, t

∞

2

Нормировка δ – функции

∫δ (t ) dt = 1

− ∞

3

Сдвиг δ – функции во времени

δ

0, t ≠ t0

(t −t0 ) =

t = t0

∞,

18

1

t0

4

Изменение масштаба времени

δ

(at −t0 ) =

δ t −

a

a

5

Умножение сигнала на δ – функцию

s (t )δ (t ) = s (0)δ (t )

s (t )δ (t − t 0 ) = s (t 0 )δ (t − t 0 )

t 2

∫s (t )δ (t ) dt = s ( 0 )

t1

Взаимодействие сигнала s(t) и δ

t

6

– функции;

∫2

s ( t )δ ( t − t 0 ) dt

= s ( t 0 )

t1 <t < t2

t1

t 2

∫

δ (τ − t )δ (τ − t 0 ) d τ = δ (t − t 0 )

t1

	7	Дифференцирование δ – функции		δ ′(t − t0 ) = 0, t ≠ t0
				t 2	t 2
				∫s(t)δ ′(t)dt	= − ∫s′(t )δ (t)dt = − s′(0)
				t1	t1
	8	Взаимодействие сигнала s(t) и производных		t2	t2
		от δ – функции;	t1 <t < t2	∫s(t)δ′(t −t0 )dt = − ∫s′(t)δ(t −t0 )dt = − s′(t0 )
				t1	t1
				t2	t2
				∫s(t)δ(n) (t −t0 )dt =(−1)n ∫s(n) (t)δ(t −t0 )dt =(−1)n s(n) (t0 )
				t1	t1
				∞	∞
		Взаимодействие	сигнала s(t) и функции	∫s (t )σ (t )dt = ∫s(t )dt
	9			−∞	0	19
		Хевисайда; 0 <τ < t		∞	t
				∫s(τ )σ (t −τ )dτ = ∫s(τ )dτ
				−∞	−∞
				∞	∞
				s(0) = ∫s(t )σ ′(t )dt = − ∫s ′(t )σ (t )dt
				−∞	−∞
		Взаимодействие	сигнала s(t) и производной	∞	∞
	10			s(t0 ) = ∫s(t )σ ′(t − t0 )dt = − ∫s ′(t )σ (t − t0 )dt
		от функции Хевисайда; 0 <τ < t		−∞	−∞
				∞	∞
				s(t ) = ∫s(τ )σ ′(t − τ )dτ = ∫s′(τ )σ (t − τ )dτ
				−∞	−∞

20

1.3 Энергетические характеристики сигналов

Электрическое колебание, представляющее собой изменение напряжения, тока, заряда или другой физической величины, называют сигналом. Все физические сигналы принимают вещественные значения s(t) . Однако, в тео-

рии сигналов и в теории цепей широко используются понятие комплексного сигнала Z&(t) , реальная часть которого совпадает с физическим сигналом s(t) :

Z&(t) = s(t) + jυ(t) .

(1.19)

Рассмотрим энергетические характеристики как вещественных, так и комплексных сигналов.

1.3.1 Энергетические характеристики вещественных сигналов

Основными энергетическими характеристиками вещественного сигнала s(t) являются: мгновенная мощность p(t) , энергия Э и средняя мощ-

ность P .

Мгновеннаямощность, выделяемаянасопротивлениинагрузки R , равна

				u2 (t)			2		(1.20)
	p(t) =			R = i				(t)R .
	Энергия и средняя мощность на интервале времени (t1 ,t2 ) определяют-
	ся выражениями (при условии R =1 Ом):
				t2	2 (t)dt ;
	Э = ∫s								(1.21)
				t1	t
				1		2
	P =				∫s2 (t)dt .				(1.22)
		t		−t
			2	1 t
						1

Энергетические характеристики суммы двух сигналов s1(t) и s2 (t)

кроме энергетических характеристик каждого сигнала содержат дополнительное слагаемое, которое определяет энергию взаимодействия этих сигналов:

p	∑	(t) =[s	(t )+ s	2	(t )]2 = p	(t) + p	2	(t) + 2 p (t);	(1.23)
		1			1			12
		t2	[s1(t )+ s2 (t )]2dt = Э1 +Э2 +2Э12 ;
		Э∑ = ∫							(1.24)
		t1

			1	t2	[s1(t )+ s2	(t )]2 dt = P1 + P2 + 2P12 .
	P∑ =			∫			(1.25)
		t2	−t1
				t1