В данном алгоритме число проделанных итераций подсчитывает параметр к, а правая часть выражения 1..4 обозначено как «fi». Точность решения – eps. Число итераций лучше ограничить.

2. Метод Ньютона

Если f(x) имеет непрерывную производную и− дважды непрерывно дифференцируемая функция, тогда, выбрав в (2.3), получаем эквивалентное уравнение. Т.е. рекуррентная последовательность метода Ньютона

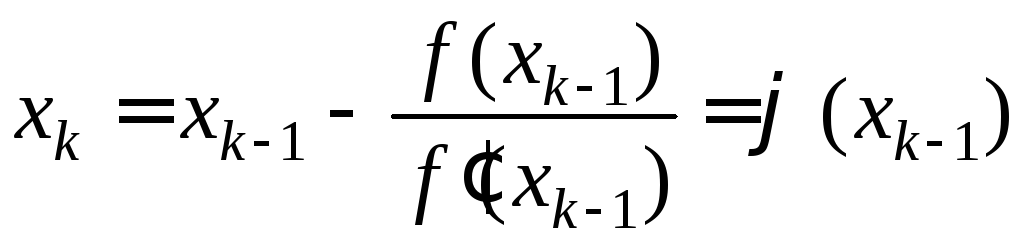(1.6)

Из (1.6) видно, что этот метод одношаговый(m=1)и для начала вычислений требуется задать одно начальное приближениеx₀изобластисходимости

при

или

при).

Метод Ньютона получил также второе название метод касательных благодаря геометрической иллюстрации его сходимости, представленной на рис. 1.2. Этот метод позволяет находить как простые, так и кратные корни.

Основной его недостаток - малая область сходимости и необходимость вычисления производной f'(x). Структурная схема алгоритма отличается от предыдущей только формулой вычисления x1 через x0.

3. Метод секущих

Данный метод является модификацией метода Ньютона, позволяющей избавиться от явного вычисления производной путем ее замены приближенной формулой. Это эквивалентно тому, что вместо касательной на рис. 1.2 проводится секущая.

Тогда вместо процесса (1.6) получаем

. (1.7)

Здесь h - некоторый малый параметр метода, который подбирается из условия наиболее точного вычисления приближенного значения производной.

Метод одношаговый (m=1)..

Рекуррентное соотношение (1.7) можно преобразовать к более простой форме.

Каждое последующее приближение вычисляется по рекуррентной формуле

,

где , (1.7а)

которая справедлива, если данная функция f(x)на интервале(, )вогнутая:().

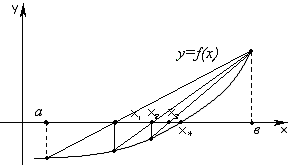
Рис. 1.3

Если же функция выпуклая, то справедлива следующая рекуррентная формула:

, (1.7б)

где (см. рис. Рис.1.4).

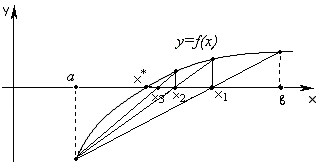
Рис. 1.4

5. Метод деления отрезка пополам

Все вышеописанные методы могут работать, если функция f(x) является непрерывной и дифференцируемой вблизи искомого корня. В противном случае они не гарантируют получение решения.

Для разрывных функций, а также. если не требуется быстрая сходимость, для нахождения простого корня на интервале (, ) применяют надежный метод деления отрезка пополам. Его алгоритм основан на построении рекуррентной последовательности по следующему закону: в качестве начального приближения выбираются границы интервала, на котором точно имеется один простой корень далее находится его серединаочередная точкаx₃ выбирается как середина того из смежных с x₂ интервалов или, на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:

1. Вычисляем .

2. Вычисляем .

3. Если тогда

иначе .

4. Если тогда повторять с п.2.

5. Вычисляем

6. Конец.

За одно вычисление функции погрешность уменьшается вдвое, то есть скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.

Варианты заданий

1. По схеме, приведенной на рис.1.7 создать и отладить программу отделения всех корней функции f(x) на указанном интервале [a, b], в соответствии с полученным вариантом из табл. 1.1.

2. Далее создать программу уточнения корня указанным итерационным методом.

Метод нахождения корня оформить в виде отдельной функции.

Выбрать точность =10^-3, =10^-4, =10^-5. Функция должна проверить правильность определения корня (f(x^*) приблизительно равна нулю).

3. Решить уравнение для выбранного интервала методом деления отрезка пополам

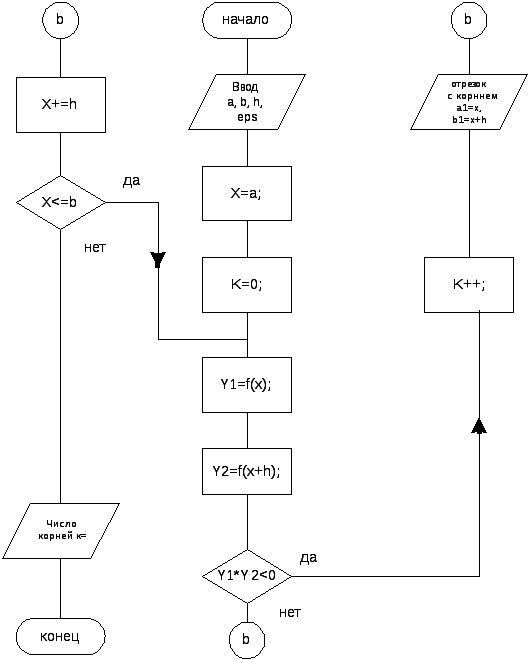
Рис.1.7

Таблица 1.1

N	f(x)	Интервал		методы
		А	B
1		-2	2	Метод деления отрезка пополам
2		-1	3	Метод секущих
3		1	8	Метод касательных
4		4	7	Метод простой итерации
5		4	8	Метод деления отрезка пополам
6		2	6	Метод секущих
7		3	9	Метод касательных
8		-4	0	Метод простой итерации
9		-12	5	Метод деления отрезка пополам
10		-2	5	Метод секущих
11		-6	2	Метод касательных
12		-4	2	Метод простой итерации
13		-7	3	Метод деления отрезка пополам
14		-4	3	Метод секущих
15		-4	4	Метод касательных

Примечание.

В табл. 1.1. все функции на указанном интервале имеют три корня.