-
Численное решение систем линейных уравнений. Метод Гаусса.
Способы решения систем линейных уравнений делятся на две группы:
1. Точные методы, представляющие собой алгоритмы для вычисления
корней системы (решение систем с помощью обратной матрицы, правило
Крамера, метод Гаусса и др.),
2. Итерационные методы, позволяющие получить решение системы с
заданной точностью путем сходящихся итерационных процессов (метод
итерации, метод Зейделя и др.).Вследствие неизбежных округлений результаты даже точных методов
являются приближенными. При использовании итерационных методов
дополнительно добавляется погрешность метода.
Метод Гаусса
Рассмотрим систему n линейных алгебраических уравнений относительно
n неизвестных х1, х2, …, хn:
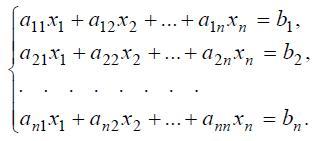
В соответствии с правилом умножения матриц рассмотренная система
линейных уравнений может быть записана в матричном виде AX=B,
Идея метода Гаусса состоит в том, что систему (8.1) представляют в виде
матрицы
которую последовательным исключением неизвестных приводят к
эквивалентной системе с треугольной матрицей вида
Эта процедура называется прямой ход. Все коэффициенты (включая d) на
каждом шаге прямого хода пересчитываются по формулам
Если в матрице встретилась строка с номером m, в которой все элементы
сmj равны нулю, а dm≠0, то выполнение алгоритма останавливаем и делаем
вывод о том, что система несовместна. Действительно, восстанавливая систему
уравнений по матрице, получим, что m-ое уравнение будет иметь вид
0 x1 + 0 x2 + 0 x3 + …. + 0 xn= dm
Этому уравнению не удовлетворяет ни один набор чисел.
Если в матрице имеются строки, содержащие одни нули, то мы имеем
альтернативные решения данной системы.
При обратном ходе последовательно вычисляются неизвестные, начиная
с xn.
Если перед началом прямого хода в исходной матрице в первой строке на
первых местах стояли нули, то необходимо найти строку, в которой в самом
левом столбце содержится элемент, отличный от нуля и поменять ее с первой
строкой местами.
-
Численное решение нелинейных уравнений. Процедура отделения корней. Метод бисекции поиска корня нелинейного уравнения.
Численное решение нелинейных уравнений.
Решение нелинейного уравнения f(x)=0 или системы нелинейных
уравнений состоит из двух этапов:
1) Отделение корней, то есть отыскание достаточно малых областей, в
каждой из которых заключен ровно один корень уравнения или системы
уравнений.
2) Вычисление каждого отделенного корня с заданной точностью.
Укажем следующие способы отделения корня:
1) Составляется таблица значений функции y=f(x) на промежутке
изменения аргумента x, и если окажется, что для соседних значений аргументов
значения функции имеют разные знаки, то корень уравнения
f(x)=0 находится между ними (правда это не говорит о том, что корень
единственный).
2) Строится график функции f(x) на промежутке изменения аргумента x;
тогда искомые корни находятся в некоторых окрестностях точек пересечения
графика с осью OX.
Кроме того, часто нужно знать начальное приближение x0 к корню x*
(который, заметим, неизвестен). В качестве этого начального приближения
берут, как правило, любую точку отрезка, на котором отделён корень,
например, его середину x0 = (a+b)/2, если описание метода не предписывает
поступить как-нибудь иначе.
Отделение корня функции при гарантии ее определения на
неограниченном интервале, может осуществляться по следующему
итерационному алгоритму.
1. Для начального приближения x0, найти f0=f(x0), задать начальный
интервал поиска D и его коэффициент расширения d>1.
2. Вычислить a=x0 -D, b=x0+D.
3. Увеличить интервал поиска: D=D*d. Если интервал превысил
некоторый заданный предел закончить поиск (интервал не найден).
57
4a. Если знаки fa и f0 отличаются, то считать корень окруженным на [a,x0] и
выйти из алгоритма.
4b. Если знаки fb и f0 отличаются, то считать корень окруженным на [x0,b] и
выйти из алгоритма.
4c. Если f0>0 (случай меньше нуля анализируется аналогично) перейти к 5:
5. Проверяется, какое значение из fa или fb является меньшим. Если оба
одинаковы, то переходим к 6a (двусторонний поиск), если fb - производим
поиск вправо 6b, иначе - поиск влево 6c.
6a. Находим a=a-D, b=b+D, fa=f(a), fb=f(b), идем к пункту 3.
6b. Присваиваем последовательно a=x0, x0=b, fa=f0, f0=fb; находим b=b+D,
fb=f(b), переходим к пункту 3.
6c. Аналогично 6b, только направление поиска - влево.
Так как интервал поиска постоянно расширяется, то в конце концов
используя указанный алгоритм корень будет локализован.
Метод бисекции (дихотомии или половинного деления).
Пусть [a,b] -
отрезок локализации. Предположим, что функция f(x) непрерывна на [a,b] и на
концах принимает значения разных знаков f(a)· f(b)<0.
Алгоритм метода бисекции состоит в построении последовательности
вложенных отрезков, на концах которых функция принимает значения разных
знаков. Каждый последующий отрезок получают делением пополам
предыдущего.
Опишем один шаг итераций метода. Пусть на k-ом шаге найден отрезок
[ak,bk] такой, что f(ak)· f(bk)<0. Найдем середину отрезка xk= (ak + bk)/2. Если
f(xk)=0, то xk - корень и задача решена. Если нет, то из двух половин отрезка
выбираем ту, на концах которой функция имеет противоположные знаки:
ak+1= ak, bk+1= xk, если f(ak)· f(xk)<0
ak+1= xk, bk+1= bk , если f(ak)· f(xk)>0
Критерий окончания итерационного процесса: если длина отрезка
локализации меньше ε, то итерации прекращают и в качестве значения корня с
заданной точностью принимают середину отрезка.