
4.1. Спектральный (гармонический) анализ сигналов
Гармонический анализ – это раздел математики, который изучает представления функций в виде тригонометрических рядов и интегралов.
В
1807 Жан Батист Жозеф Фурье высказал идею
о том, что периодическая функция (2.1)
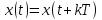 может быть представлена в виде
синусоидальных и/или косинусоидальных
функций различных частот, умноженных
на некоторые коэффициенты.
может быть представлена в виде
синусоидальных и/или косинусоидальных
функций различных частот, умноженных
на некоторые коэффициенты.
4.1.1. Инвариантность синусоиды
Если входной сигнал – это гармоническое колебание (функция времени синусоида/косинусоида) (2.2)
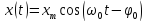 ,
,
то
выходной сигнал линейной системы будет
также синусоидальный
той же частоты
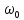 ,
хотя амплитуда
,
хотя амплитуда
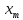 и начальная фаза
и начальная фаза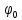 могут отличаться от первоначальных
значений. Таким образом, форма сигнала
сохраняется, так как в линейной системе
с сигналом возможны только такие операции
как умножение на постоянную величину,
дифференцирование, интегрирование,
задержка и суммирование.
могут отличаться от первоначальных
значений. Таким образом, форма сигнала
сохраняется, так как в линейной системе
с сигналом возможны только такие операции
как умножение на постоянную величину,
дифференцирование, интегрирование,
задержка и суммирование.
На практике используют и иные способы представления сигналов. В отображении сигналов, наряду с синусоидальной функцией, широко применяется комплексная экспоненциальная функция вида
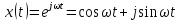 .
(4.1)
.
(4.1)
Рисунок 4.1 иллюстрирует графическое представление этой функции.
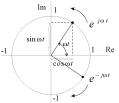
Рисунок 4.1
Функция
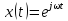 отражает положение комплексного числа
отражает положение комплексного числа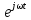 на единичной окружности в комплексной
плоскости, где на оси абсцисс представлена
его действительная часть, а на оси
ординат – его мнимая часть. Выражению
на единичной окружности в комплексной
плоскости, где на оси абсцисс представлена
его действительная часть, а на оси
ординат – его мнимая часть. Выражению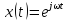 соответствует точка, расположенная на
единичной окружности в комплексной
плоскости. Прямая, соединяющая эту точку
с началом координат комплексной плоскости
образует с действительной осью угол
соответствует точка, расположенная на
единичной окружности в комплексной
плоскости. Прямая, соединяющая эту точку
с началом координат комплексной плоскости
образует с действительной осью угол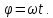 Точка движется по окружности против
часовой стрелки со скоростью
Точка движется по окружности против
часовой стрелки со скоростью
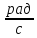 – поэтому
– поэтому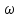 называют круговой частотой. Выражение
называют круговой частотой. Выражение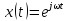 представляет
собой единичный вектор, угол которого
линейно нарастает со временем со
скоростью
представляет
собой единичный вектор, угол которого
линейно нарастает со временем со
скоростью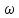
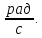 Выражение
Выражение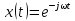 соответствует вектору, угол которого
линейно нарастает со временем в
противоположном направлении с той же
скоростью
соответствует вектору, угол которого
линейно нарастает со временем в
противоположном направлении с той же
скоростью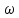
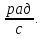 Поскольку
Поскольку
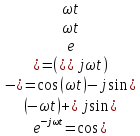 *,
*,
то
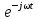 и
и
 являются сопряженными функциями.
являются сопряженными функциями.
4.1.2. Представление периодической функции рядом Фурье
Основным
понятием в гармоническом анализе
является гармоническое колебание.
В гармоническом
анализе вводится понятие n-й
гармоники
периодического
колебания частоты
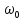 ,
под которой понимаютгармоническое
колебание с частотой, в п
раз превышающей
основную частоту
,
под которой понимаютгармоническое
колебание с частотой, в п
раз превышающей
основную частоту
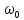 .
Например,
.
Например,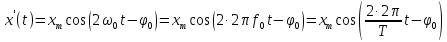 выполняет два колебания за каждые
выполняет два колебания за каждые
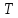 секунд.
секунд.
Следующим важным понятием является спектр сигнала. Под спектром сигнала понимают совокупность его гармонических составляющих. Введение понятия спектра сигнала обусловило использование в технических приложениях название спектрального анализа для гармонического анализасигналов.
Как
известно, любой сигнал
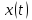 ,
описываемый периодической функцией
времени, удовлетворяющей условиям
Дирихле (модели реальных сигналов им
удовлетворяют), можно представить в
виде суммы гармонических колебаний,
называемой рядом Фурье:
,
описываемый периодической функцией
времени, удовлетворяющей условиям
Дирихле (модели реальных сигналов им
удовлетворяют), можно представить в
виде суммы гармонических колебаний,
называемой рядом Фурье:
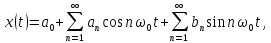 (4.2)
(4.2)
где
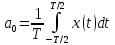 – среднее значение сигнала за период
или постоянная составляющая сигнала,
{
– среднее значение сигнала за период
или постоянная составляющая сигнала,
{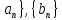 – множества коэффициентов.
– множества коэффициентов.
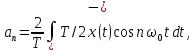 (4.3)
(4.3)
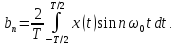 (4.4)
(4.4)
Из
формул (4.2 – 4.4) следует, что функцию
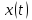 можно представить множеством действительных
чисел {
можно представить множеством действительных
чисел {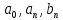 }.
}.
4.1.3. Комплексная форма ряда Фурье
С
целью упрощения расчетов часто используют
вместо тригонометрической формы записи
ряда Фурье его комплексную форму. Расчет
спектров сигналов в комплексной области
значительно проще, поскольку нет
необходимости рассматривать отдельно
коэффициенты
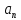 и
и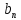 тригонометрической формы записи ряд
Фурье.
тригонометрической формы записи ряд
Фурье.
С учетом формул Эйлера
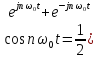 ),
),
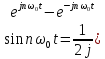 ),
),
где
 – комплексная экспоненциальная функция,
– комплексная экспоненциальная функция,
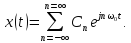
В
этом случае
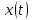 определяется множеством комплексных
чисел
определяется множеством комплексных
чисел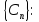
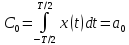
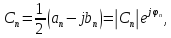
где


Совокупность
комплексных амплитуд
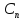 называют комплексным спектром
периодического сигнала. На рисунке 4.1
показана геометрическая интерпретация
комплексного числа
называют комплексным спектром
периодического сигнала. На рисунке 4.1
показана геометрическая интерпретация
комплексного числа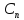 .
.
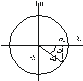
Рисунок 4.1
Угол
 отражает ориентацию комплексного
вектора относительно направления
действительной оси.
отражает ориентацию комплексного
вектора относительно направления
действительной оси.
Совокупность
значений
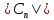 иnназывается спектром периодической
функции. Амплитуды гармоник
иnназывается спектром периодической
функции. Амплитуды гармоник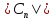 характеризуют амплитудный спектр, а
начальные фазы
характеризуют амплитудный спектр, а
начальные фазы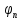 –
фазовый спектр.
–
фазовый спектр.
Таким образом, спектр периодического сигнала представляется в виде постоянной составляющей и бесконечного числа гармонических колебаний (синусоидальных или косинусоидальных) с соответствующими амплитудами и начальными фазами.На рисунках 4.1 и 4.2 приведены амплитудный и фазовый спектры некоторого периодического сигнала.
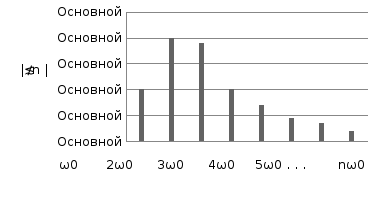
Рисунок 4.1– Амплитудный спектр сигнала
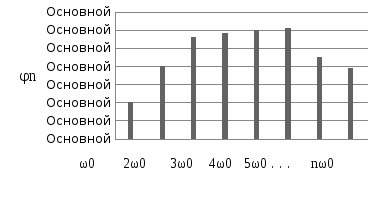
Рисунок 4.2– Фазовый спектр сигнала
Каждая гармоническая составляющая изображена вертикальными отрезками, длины которых (в некотором масштабе) равны ее амплитуде и фазе. Как видно, спектр периодического сигнала является дискретным или, как говорят, линейчатым. Частоты всех гармоник кратны основной частоте. Это означает, что если периодический сигнал следует с частотой, например, 1 кГц, то в его спектре могут быть только частоты 0кГц, 1 кГц, 2 кГц и т.д. В спектре такого периодического сигнала не могут присутствовать, например, частоты 1,5 кГц или 1,2 кГц.
4.2. Преобразование Фурье
Когда функция не является периодической (но площадь под графиком ее модуля конечна), она может быть выражена в виде интеграла от синусов и/или косинусов, умноженных на некоторую весовую функцию, а именно
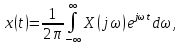 (4.5)
(4.5)
где
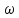 непрерывная круговая частота. Поскольку
непрерывная круговая частота. Поскольку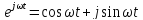 ,
преобразование (4.5) основано на множестве
синусоидальных функций. Имеется аналогия
между функцией
,
преобразование (4.5) основано на множестве
синусоидальных функций. Имеется аналогия
между функцией
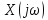 и коэффициентами ряда Фурье. Функция
и коэффициентами ряда Фурье. Функция
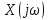 называется частотным спектром сигнала.
называется частотным спектром сигнала.
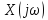 указывает вес, который придается
выражению
указывает вес, который придается
выражению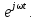
Определение
4.1. Прямое преобразование
Фурье (Фурье-образ) непрерывной функции
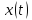 называется функция
называется функция
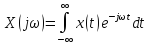 .
(4.6)
.
(4.6)
Значение
функции
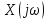 в
области ее определения определяется
интегралом
по всем значениям функции
в
области ее определения определяется
интегралом
по всем значениям функции
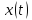 .
В свою очередь, значения
функции
.
В свою очередь, значения
функции
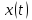 умножаются на синусы и косинусы разных
частот. Область значений переменной
умножаются на синусы и косинусы разных
частот. Область значений переменной
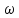 ,
на которой принимает свои значения
функция
,
на которой принимает свои значения
функция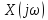 ,
называется частотной областью, поскольку
значение переменной
,
называется частотной областью, поскольку
значение переменной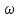 определяет частоты составляющих
преобразование. Значения переменной
определяет частоты составляющих
преобразование. Значения переменной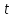 также влияет на частоты, но так как по
этой переменной производится
интегрирование, это влияние одинаково
для всех значений переменной
также влияет на частоты, но так как по
этой переменной производится
интегрирование, это влияние одинаково
для всех значений переменной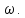 Преобразование
Фурье можно представить призмой, которая
разлагает функцию
Преобразование
Фурье можно представить призмой, которая
разлагает функцию
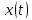 на различные составляющие в зависимости
от ее частотного содержания. Преобразование
Фурье описывает функцию с помощью
совокупности составляющих ее частот.
на различные составляющие в зависимости
от ее частотного содержания. Преобразование
Фурье описывает функцию с помощью
совокупности составляющих ее частот.
Определение
4.2. Функция
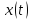 может быть полностью восстановлена при
помощи обратного преобразования Фурье
(4.5).
может быть полностью восстановлена при
помощи обратного преобразования Фурье
(4.5).
Это свойство позволяет работать в Фурье-области, а затем вернуться
во временную область определения функции без потери информации. Так как любая функция может быть представлена совокупностью синусоид и/или косинусоид, линейное преобразование произвольного сигнала может анализироваться в три этапа:
– представлять сигнал в виде комбинации синусоид;
– рассчитывать отклик на каждую из этих отдельных синусоид;
– комбинировать отдельные результаты.
4.3. Дискретная комплексная экспоненциальная последовательность
В
цифровых системах сигналы определяются
лишь для дискретных значений времени
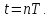 В этом случае сигнал
В этом случае сигнал
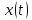 (4.1), записанный каккомплексная
экспоненциальная функция,
преобразуем следующим
образом:
(4.1), записанный каккомплексная
экспоненциальная функция,
преобразуем следующим
образом:
 (4.7)
(4.7)
Для нормированной частоты
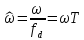
выражение (4.7) можно представить в виде
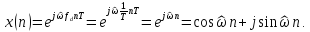 (4.8)
(4.8)
Определение
4.3. Функция
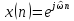 называется дискретнойкомплексной
экспоненциальной последовательностью.
называется дискретнойкомплексной
экспоненциальной последовательностью.
Вещественная
и мнимая часть последовательности
(4.8)
меняется синусоидально в зависимости
от
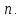 По аналогии с непрерывным временем
параметр
По аналогии с непрерывным временем
параметр называется круговой частотойдискретной
комплексной экспоненты. В формуле (4.8)
частота
называется круговой частотойдискретной
комплексной экспоненты. В формуле (4.8)
частота
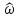 измеряется в радианах.
измеряется в радианах.
4.3. Дискретизированное по времени преобразование Фурье
Пара
преобразований Фурье для дискретизированного
сигнала
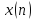 имеет вид
имеет вид
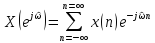 ,
(4.8)
,
(4.8)
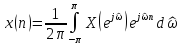 .
(4.9)
.
(4.9)
Для
упрощения записи формул преобразования
Фурье далее используется обозначение
нормированной
частоты
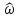 как
как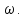 Тогда формула
Тогда формула
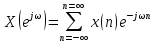 (4.10)
(4.10)
определяет
дискретизированное
по времени прямое преобразование
Фурье или Фурье-образ последовательности
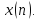
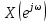 называют также спектральной функцией.
Поскольку
называют также спектральной функцией.
Поскольку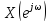 – непрерывная периодическая функция
частоты, она может быть выражена рядом
Фурье. Формула (4.10) представляет собой
разложение периодической функции
– непрерывная периодическая функция
частоты, она может быть выражена рядом
Фурье. Формула (4.10) представляет собой
разложение периодической функции в виде ряда Фурье, в котором коэффициентами
Фурье являются значения отсчетовпоследовательности
в виде ряда Фурье, в котором коэффициентами
Фурье являются значения отсчетовпоследовательности
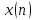 .
.
Формулу
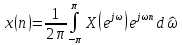 (4.11)
(4.11)
называют обратным преобразованием Фурье.
Обратное
преобразование
Фурье (4.11) можно трактовать как
представление последовательности
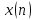 черезнепрерывную
периодическую функцию частоты
черезнепрерывную
периодическую функцию частоты
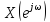 .Последовательность
.Последовательность
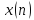 можно рассматривать в виде суперпозиции
экспоненциальных сигналов с комплексными
амплитудами
можно рассматривать в виде суперпозиции
экспоненциальных сигналов с комплексными
амплитудами
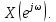
Замечание. Пара преобразований Фурье существует только тогда, когда ряд (4.10) сходится.
Фурье-образ
последовательности
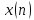 в алгебраической и показательной форме
записывается как
в алгебраической и показательной форме
записывается как
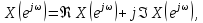 (4.12)
(4.12)
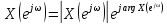 .
(4.13)
.
(4.13)
Совокупность
значений
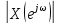 и
и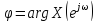 характеризуют амплитудный спектр и
фазовый спектрпоследовательности
характеризуют амплитудный спектр и
фазовый спектрпоследовательности

4.4. Дискретное преобразование Фурье
4.4.1. Конечные дискретные комплексные экспоненциальные функции
Как отмечалось ранее, для описания дискретных линейных стационарных систем в континуальном спектральном анализе используются дискретные комплексные экспоненциальные последовательности вида

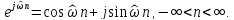 (4.14)
(4.14)
Данная
система функций составляет счетное
бесконечное множество и определена на
бесконечном интервале частоты

Экспоненциальная
последовательность может быть задана
на конечном интервале времени
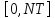 ,
где
,
где
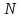 – целое положительное число. Тогда
величина
– целое положительное число. Тогда
величина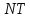 определяет основной периоддискретной
комплексной экспоненциальной
последовательности. В этом случае
значение
определяет основной периоддискретной
комплексной экспоненциальной
последовательности. В этом случае
значение
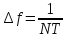 –основная
линейная частота последовательности.
Основная
круговая частота
–основная
линейная частота последовательности.
Основная
круговая частота

определяет
период дискретизации по частоте.
Абсолютное значение непрерывной частоты
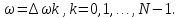 Далее преобразуем сигнал
Далее преобразуем сигнал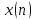 (4.14)следующим
образом:
(4.14)следующим
образом:
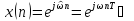
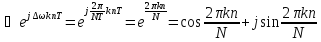 .
(4.15)
.
(4.15)
В дискретном преобразовании Фурье используется система комплексных дискретных экспоненциальные функции (ДЭФ), определяемых выражением
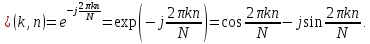
Введем
обозначение
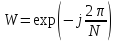 .
Тогда
.
Тогда
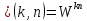 .
.
Переменная
 называется поворачивающим множителем.
Переменные
называется поворачивающим множителем.
Переменные и
и принимают целочисленные значения
принимают целочисленные значения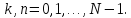 Так как показатель степени комплексного
числа
Так как показатель степени комплексного
числа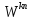 со
знаком „плюс“, то функция
со
знаком „плюс“, то функция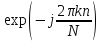 описывает точку, которая движется по
окружности в направлении часовой
стрелки. В выражении (4.15) переменные
времени и частоты изменяются дискретно,
в отличие от (4.14), где время изменяется
дискретно, а частота непрерывно. Заметим,
что огибающая дискретных значенийфункции
описывает точку, которая движется по
окружности в направлении часовой
стрелки. В выражении (4.15) переменные
времени и частоты изменяются дискретно,
в отличие от (4.14), где время изменяется
дискретно, а частота непрерывно. Заметим,
что огибающая дискретных значенийфункции
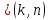 соответствуетфункции
соответствуетфункции
 Рисунок
4.3 иллюстрирует графическое представление
этой функции.
Рисунок
4.3 иллюстрирует графическое представление
этой функции.
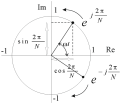
Рисунок 4.3
Если
переменная
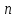 последовательно принимает значения
последовательно принимает значения то через
то через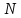 шагов, комплексный вектор проходит
шагов, комплексный вектор проходит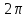 радиан или совершает один оборот на
комплексной плоскости. Вращаясь, вектор
ДЭФ занимает на плоскости только
радиан или совершает один оборот на
комплексной плоскости. Вращаясь, вектор
ДЭФ занимает на плоскости только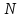 фиксированных положений. Выражение
фиксированных положений. Выражение представляет собой единичный вектор
на комплексной плоскости, угол которого
линейно нарастает со временем. Модуль
комплексного числа
представляет собой единичный вектор
на комплексной плоскости, угол которого
линейно нарастает со временем. Модуль
комплексного числа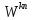 равен
равен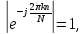 а его аргумент
а его аргумент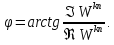
Пример
4.1. Пусть
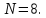 Значения фазы
Значения фазы
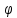 вектора ДЭФ для
вектора ДЭФ для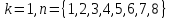 соответственно равны
соответственно равны Следовательно, при увеличении
Следовательно, при увеличении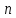 фаза ДЭФ нарастает по линейному закону.
фаза ДЭФ нарастает по линейному закону.
Пример
4.2. Пусть
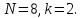 Значения фазы
Значения фазы
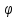 вектора ДЭФ для
вектора ДЭФ для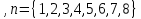 соответственно равны
соответственно равны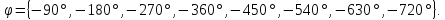
Через
8 шагов комплексный вектор проходит
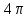 радиан или совершает два оборота на
комплексной плоскости за тоже время
(пример
4.1)
радиан или совершает два оборота на
комплексной плоскости за тоже время
(пример
4.1)
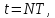
где
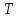 –
интервал дискретизации.
–
интервал дискретизации.
Скорость
нарастания фазы
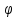 вектора ДЭФ определяет номер
вектора ДЭФ определяет номер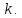 Можно сказать, что фаза ДЭФ нарастает
со скоростью
Можно сказать, что фаза ДЭФ нарастает
со скоростью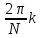 радиан. В примере 4.2 со скоростью
радиан. В примере 4.2 со скоростью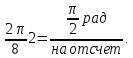
Величина
полной фазы за дискретное время
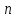 определяется как
определяется как

где
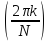 – скорость изменения фазы ДЭФ или
частота этой функции. Таким образом,
частота ДЭФ – это число оборотов,
совершаемых вектором ДЭФ на интервале
ее определения
– скорость изменения фазы ДЭФ или
частота этой функции. Таким образом,
частота ДЭФ – это число оборотов,
совершаемых вектором ДЭФ на интервале
ее определения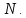
Пример 4.3. Вычисление значений ДЭФ.
1.
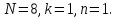
Решение.
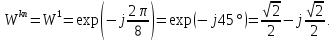
2.
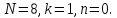
Решение.
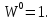
3.
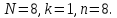
Решение.
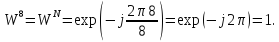
4.
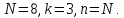
Решение.

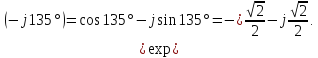
На рисунке 4.4 показаны положения вектора ДЭФ на комплексной плоскости примера 4.3.
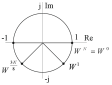
Рисунок 4.4
Систему
ДЭФ записывают в виде матрицы
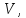 строки которой нумеруются переменной
строки которой нумеруются переменной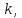 столбцы переменной
столбцы переменной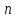 .
В пересечении -й строки и
.
В пересечении -й строки и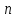 -го
столбца записывается величина
-го
столбца записывается величина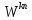 :
:
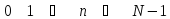
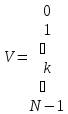
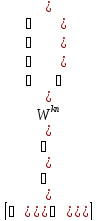 .
.
Например,
для
 матрица
матрица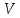 имеет следующий вид:
имеет следующий вид:
 .
(4.16)
.
(4.16)
Если
подставить в эту матрицу числовые
значения степенного ряда
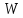 ,
то
,
то
получим
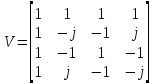 .
(4.17)
.
(4.17)
На рисунке 4.5 показаны положения вектора ДЭФ и ее значения на комплексной плоскости, соответствующие матрице (4.17).
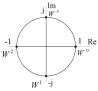
Рисунок 4.5
4.4.2. Свойства дискретных экспоненциальных функций
1.
Функции
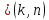 ортогональны, т.е.
ортогональны, т.е.
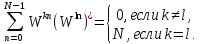 (4.18)
(4.18)
Так
как
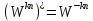 ,
то
,
то
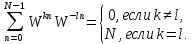
Следствием свойства ортогональности является:
– скалярное
произведение различных двух строк
матрицы
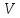 ,
одна из которых должна быть комплексно
сопряженной, равно нулю;
,
одна из которых должна быть комплексно
сопряженной, равно нулю;
– скалярное
произведение одинаковых двух строк
матрицы
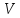 ,
одна из которых должна быть комплексно
сопряженной, равно
,
одна из которых должна быть комплексно
сопряженной, равно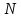 .
.
Действительно,
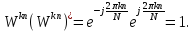 Сумма
Сумма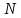 единиц даст число
единиц даст число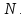
Матричная запись свойства ортогональности имеет вид
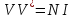 ,
,
где
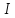 –
единичная
матрица.
–
единичная
матрица.
2. Периодичность:
если
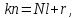 то
то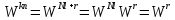 .
(4.19)
.
(4.19)
Поскольку
ДЭФ являются периодическими функциями,
матрицу (4.16) можно переписать с минимальными
фазами
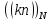 ,
образующимися после вычитания из
значения
,
образующимися после вычитания из
значения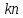 целого числа периодов
целого числа периодов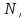 т.е.
т.е.
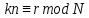 .
.
Для
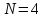 матрицу ДЭФ (4.16) с минимальными фазами
матрицу ДЭФ (4.16) с минимальными фазами
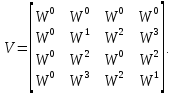
3. Симметричность.
ДЭФ
является функцией двух переменных
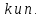 Выводы относительно одной из переменных
справедливы и для другой. Тогда
Выводы относительно одной из переменных
справедливы и для другой. Тогда
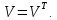
4. Обратная матрица ДЭФ.
Из
свойства ортогональности
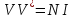 .
Умножим обе части этого равенства слева
на
.
Умножим обе части этого равенства слева
на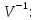
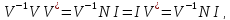
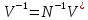 .
(4.20)
.
(4.20)
5. Мультипликативность:
– по
строкам
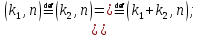
– по
столбцам
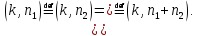
Действительно,
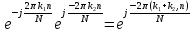 .
При умножении любых двух строк (столбцов)
матрицы
.
При умножении любых двух строк (столбцов)
матрицы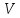 получается
строка (столбец) той же матрицы. Номер
полученной строки (столбца) равен сумме
номеров сомножителей.
получается
строка (столбец) той же матрицы. Номер
полученной строки (столбца) равен сумме
номеров сомножителей.
4.4.3. Определение дискретного преобразования Фурье
Прямое
дискретное преобразование Фурье (ДПФ)
последовательности
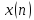 определяется как дискретная
последовательности
определяется как дискретная
последовательности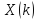 в частотной области (экспоненциальная
форма)
в частотной области (экспоненциальная
форма)
 (4.21)
(4.21)
где
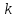 – индексДПФ
в частотной области,
– индексДПФ
в частотной области,
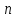 – временной входной последовательности
отсчетов сигнала.
– временной входной последовательности
отсчетов сигнала.
Дискретное преобразование Фурье устанавливает связь между временным и частотным представлениями сигнала при разложении его по конечным дискретным экспоненциальным функциям.
Обратное ДПФ (ОДПФ) имеет следующий вид:
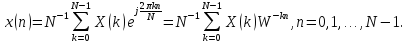 (4.22)
(4.22)
Взаимная
обратимость выражений (4.21) и (4.22)
доказывается подстановкой
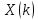 в
в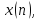 т.е.
т.е.
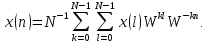 (4.23)
(4.23)
Так
как
 не зависит от
не зависит от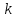 ,
изменяем порядок суммирования в (4.23),
,
изменяем порядок суммирования в (4.23),
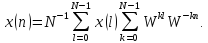 (4.24)
(4.24)
В
силу ортогональность ДЭФ внутренняя
сумма отлична от нуля только при
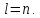 В этом случае, правая часть выражения
(4.24) равна
В этом случае, правая часть выражения
(4.24) равна
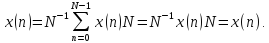
Тригонометрическая форма ДПФ:
прямое ДПФ
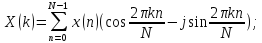
обратное ДПФ
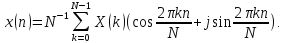
Замечание.
Принципиальное различие между
дискретизированным по времени
преобразованием
Фурье и ДПФ обусловлено характером
системы функций
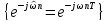 и {
и {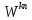 },
а именно:
},
а именно:
–
огибающая
дискретных значений функции
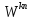 соответствует функции
соответствует функции
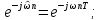
–
конечный
интервал времени
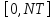 задания
функции
задания
функции
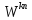 ;
;
–
периодической
структурой отсчетов восстанавливаемой
последовательности
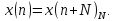
4.4.4. Свойства дискретного преобразования Фурье
1.
Периодичность. Свойство периодичности
ДЭФ
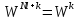 приводит к выражениям
приводит к выражениям

Действительно,

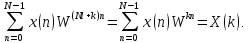
Обычно
ограничиваются рассмотрением одного
периода длиной
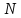 во временной и в частотной области. Это
позволяет определить матричную форму
ДПФ:
во временной и в частотной области. Это
позволяет определить матричную форму
ДПФ:
– прямое
ДПФ
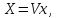 (4.25)
(4.25)
где
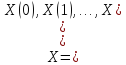 и
и –
векторы
–
векторы
отсчетов последовательности спектральных коэффициентов и сигнала соответственно;
– обратное
ДПФ
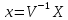 .
Используя формулу (4.20), получаем
.
Используя формулу (4.20), получаем
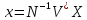 .
(4.26)
.
(4.26)
2.
Линейность. Класс
линейных систем определяется линейными
операциями или принципом суперпозиции.
Если
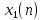 и
и
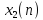 входные последовательности, а
входные последовательности, а
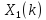 и
и
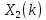 соответственно их ДПФ,
то при подаче на вход последовательности
соответственно их ДПФ,
то при подаче на вход последовательности
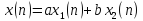 систему называют линейной тогда и только
тогда, когда выполняется
систему называют линейной тогда и только
тогда, когда выполняется
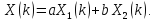
где
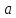 и
и произвольные постоянные параметры
(константы). Спектр последовательности
произвольные постоянные параметры
(константы). Спектр последовательности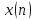 равен
равен


3. Инвариантность ДПФ относительно сдвига по времени и частоте:
1.
Инвариантность относительно циклического
сдвига по времени. Если последовательность
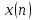 имеет ДПФ
имеет ДПФ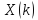 ,
то ДПФ последовательности
,
то ДПФ последовательности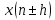 равно
равно
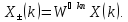
Рассмотрим
две последовательности
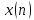 и
и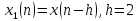 .
Формы последовательности показаны на
рисунке 4.6.а,б.
.
Формы последовательности показаны на
рисунке 4.6.а,б.
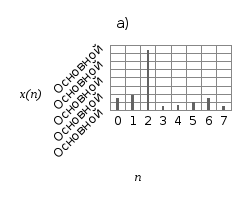
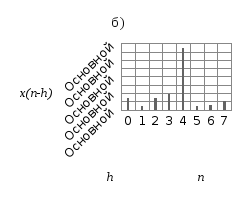
Рисунок 4.6
ДПФ
последовательности
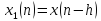 равно
равно
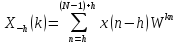 .
.
Заменяя
индекс суммирования
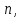 и введя новую переменную
и введя новую переменную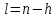 ,
получим
,
получим
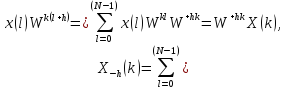
где
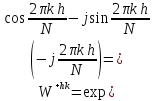 ).
Тогда
).
Тогда
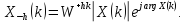
Таким образом, при сдвиге дискретного сигнала по времени изменениям подвергаются только фазы дискретных функций (фазовый спектр), амплитудный спектр не изменяется.
2.
Инвариантность относительно сдвига по
частоте. Если спектральной последовательности
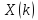 соответствует последовательность
соответствует последовательность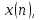 то при сдвиге последовательности
то при сдвиге последовательности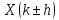 исходная последовательность
исходная последовательность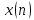 получит фазовый сдвиг, т.е.
получит фазовый сдвиг, т.е.
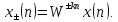
Пусть
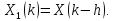 ОбратноеДПФ
последовательности
ОбратноеДПФ
последовательности
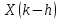 равно
равно
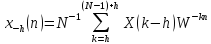 .
.
Заменяя
индекс суммирования
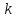 ,
и введя новую переменную
,
и введя новую переменную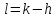 ,
получим
,
получим
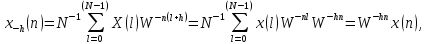
где
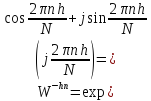 ).
).
4.
Теорема о свертке. Если исходные
последовательности отсчетов сигналов
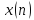 и
и имеют конечные периоды
имеют конечные периоды ,
их циклическая свертка определяется
формулой
,
их циклическая свертка определяется
формулой
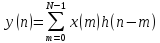 ,
𝑛
= 0, 1,…, 𝑁–1.
,
𝑛
= 0, 1,…, 𝑁–1.
Вычислим
ДПФ последовательности
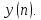
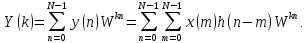 (4.27)
(4.27)
Так
как
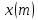 не зависит от
не зависит от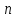 ,
изменяем порядок суммирования в (4.27).
,
изменяем порядок суммирования в (4.27).
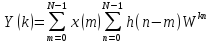 .
(4.28)
.
(4.28)
Используя свойство инвариантности относительно циклического сдвига по времени, можно записать составляющую выражения (4.28) как
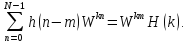
Тогда
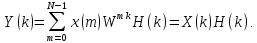 (4.29)
(4.29)
Таким образом, спектр свертки равен произведению спектров сворачиваемых последовательностей. Коэффициенты свертки вычисляются на основе ОДПФ по формуле
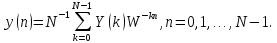
Теорема (4.29) позволяет вычислить коэффициенты свертки при помощи ДПФ по формуле
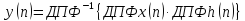 .
.
При больших величинах 𝑁 на практике применяют эффективные алгоритмы вычисления свертки с использованием быстрых преобразований Фурье.
5.
Теорема о корреляции. По определению
(2.13) корреляционная функция двух
конечных последовательностей
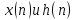 равна
равна
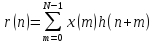 ,
для 𝑛
= 0, 1,…,𝑁–1.
,
для 𝑛
= 0, 1,…,𝑁–1.
Вычислим
ДПФ последовательности

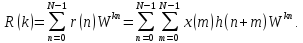 (4.30)
(4.30)
Так
как
 не зависит от
не зависит от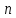 ,
изменяем порядок суммирования в (4.30).
,
изменяем порядок суммирования в (4.30).
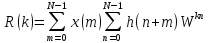 .
(4.31)
.
(4.31)
Используя свойство инвариантности относительно циклического сдвига по времени , можно записать составляющую выражения (4.31) как
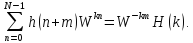
Тогда
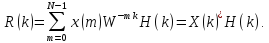 (4.32)
(4.32)
Таким образом, спектр корреляционной функции равен произведению спектров сворачиваемых последовательностей, причем один из спектров берется в комплексном сопряжении.
Коэффициенты корреляционной функции вычисляются на основе ОДПФ по формуле
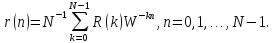
Теорема (4.32) позволяет вычислить коэффициенты корреляционной функции при помощи ДПФ по формуле
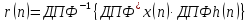 .
.
На практике применяют эффективные алгоритмы вычисления корреляционной функции с использованием быстрых преобразований Фурье.
6.
Теорема Парсеваля. Пусть последовательности
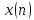 и
и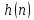 будут идентичными. В этом случае теорема
о корреляции записывается как
будут идентичными. В этом случае теорема
о корреляции записывается как
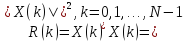 .
.
Коэффициенты корреляционной функции, вычисляются на основе выражения ОДПФ, т.е.
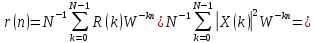
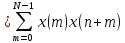 (4.33)
(4.33)
В
частном случае, для
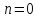 равенство (4.33) сводится к соотношению
равенство (4.33) сводится к соотношению
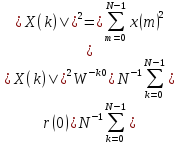 ,
,
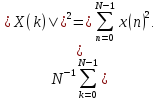 (4.34)
(4.34)
Из
(4.34) следует, что энергия сигнала,
вычисленная во временной области (по
переменной
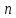 )
равна энергии сигнала, вычисленной в
частотной области. Каждая величина
)
равна энергии сигнала, вычисленной в
частотной области. Каждая величина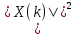 представляет собой мощность дискретной
гармоники, имеющей частоту с номером
представляет собой мощность дискретной
гармоники, имеющей частоту с номером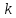 .
.
5. Предварительное задание
5.1. Вычислить значения ДЭФ:
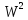 ,
,
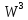 ,
,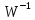
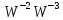 при
при
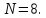
5.2.
Функции системы ДЭФ записать в виде
матрицы
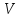 размерностью
размерностью
5.3. Вычислить спектр дискретизированного сигнала, показанного на рисунке 5.1, с помощью ДПФ. Построить графики амплитудного и фазового спектров.
5.4. По полученным значениям ДПФ с помощью ОДПФ восстановить исходные значения отсчетов сигнала.
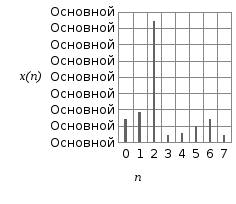
Рисунок 5.1
5.4. По полученным значениям ДПФ с помощью ОДПФ восстановить исходные значения отсчетов сигнала.
5.5.
Вычислить автокорреляционную функцию
(АКФ)
последовательности
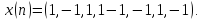 Построить графики входного сигнала и
АКФ.
Построить графики входного сигнала и
АКФ.
5.6.
Вычислить
автосвертку последовательности
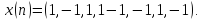 Построить график свертки.
Построить график свертки.
6. Лабораторное задание
6.1. Провести вычисления, подтверждающие свойства 1, 2, 5 дискретных экспоненциальных функций.
6.2.
Вычислить спектр дискретизированного
сигнала (п. 5.3), сдвинутого по времени на
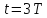 интервалов дискретизации. Построить
графики сигнала, амплитудного и фазового
спектров.
интервалов дискретизации. Построить
графики сигнала, амплитудного и фазового
спектров.
6.3. По полученным значениям ДПФ с помощью ОДПФ восстановить значения отсчетов сигнала (п. 6.2). Построить график восстановленного дискретизированного сигнала.
6.4. Используя исходные данные, полученные у преподавателя, вычислить корреляционную функцию:
– по определению;
– с помощью ДПФ. Построить график КФ.
6.5. Используя исходные данные (п. 6.4) вычислить свертку:
– по определению;
– с помощью ДПФ. Построить график свертки.
6.6. Используя исходные данные (п. 6.4), провести вычисления, подтверждающие теорему Парсеваля.
7. Содержание отчета
7.1. Решение задач предварительного задания.
7.2. Расчеты и графики лабораторного задания.
7.3. Анализ результатов и выводы.
8. Контрольные вопросы
8.1. При каких условиях возможно представление непрерывного сигнала его дискретными значениями?
8.2. Что выражает корреляционная функция (АКФ, ВКФ)?
8.3. Поясните метод спектрального анализа.
8.4. Поясните понятие «спектр сигнала».
8.5. Поясните понятие « разложение сигнала в ряд Фурье».
8.6. При каких условиях точность приближения сигнала рядом Фурье повышается?
8.7. Поясните различия комплексной экспоненциальной функции, дискретной комплексной экспоненциальной функции и конечной дискретной комплексной экспоненциальной функции.
8.8. Поясните свойства ДЭФ.
8.9. Поясните свойства ДПФ.
8.10. Поясните различия ряда Фурье, преобразования Фурье, дискретизированного по времени преобразования Фурье и дискретного преобразования Фурье.
Литература
1. Оппенгейм А., Шафер Р. Цифровая обработка сигналов.– М.: Техносфера, 2006.
2. Теория прикладного кодирования: Учеб. пособие. В 2 т. В.К. Конопелько, 3. Айфичер Э.С., Джервис Б.У. Цифровая обработка сигналов: практический подход: Пер. с англ. ‒ М.: Издательский дом «Вильямс», 2008.
4. Овсянников В.А. Методы формирования и цифровой обработки сигналов. Учебное пособие для студентов специальности «Радиосвязь, радиовещание и телевидение» в 2-ух частях. ‒ Мн.: БГУИР 2010.
5. Лайонс Р. Цифровая обработка сигналов.- М.: Бином-Пресс, 2006.
6. Смит С. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников: Пер. с англ. ‒ М.: Додека-XXI, 2008.7. Сергиенко А.Б. Цифровая обработка сигналов/ А.Б. Сергиенко-СПб.: Питер, 2003.
8. Основы цифровой обработки сигналов: Курс лекций. А.И. Солонина, Улахович Д.А. и др. - СПб: БХВ – Петербург, 2003.
9. Лосев В.В. Микропроцессорные устройства обработки информации. Алгоритмы цифровой обработки: Учебное пособие для вузов. – Мн: Выш. школа, 1990.
5. Быстрое преобразование Фурье
Существует два класса алгоритмов вычисления преобразования Фурье обычное дискретное преобразование Фурье и быстрое дискретное преобразование Фурье (БПФ). Быстрый алгоритм позволяет эффективно вычислять ДПФ. При этом сокращается количество выполняемых арифметических операций, а также объем памяти, необходимый для вычисления ДПФ. В результате многие задачи спектрального анализа, обработки сигналов за счет уменьшения вычислительной сложности решаются в реальном времени.
5.1. Вычислительная сложность дискретного преобразования Фурье
Рассмотрим матричную форму ДПФ (4.25), (4.26):
– прямое
ДПФ
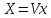 ,
,
– обратное
ДПФ
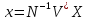 .
.
Если
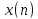 – комплекснозначная последовательность,
то для вычисления одного коэффициента
ДПФ потребуется выполнить
– комплекснозначная последовательность,
то для вычисления одного коэффициента
ДПФ потребуется выполнить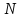 умножений и
умножений и сложений комплексных чисел, т.е. сложность
оценивается как
сложений комплексных чисел, т.е. сложность
оценивается как
комплексных
умножений
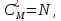
комплексных
сложений
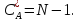
2.4.3. Дискретное преобразование Уолша-Адамара
Пусть
сигнал
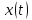 представлен
совокупностью своих равноотстоящих
отсчетов),
представлен
совокупностью своих равноотстоящих
отсчетов),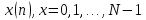 .
Выражения
.
Выражения
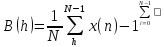
|
B(h)= |
(13)
|
|
S(x)= |
(14)
|
образуют пару дискретных преобразований Уолша-Адамара в показательной форме, формула (13) называется прямым преобразованием Уолша-Адамара (ДПУА) и дает спектр сигнала в базисе Уолша, формула (14) называется обратным преобразованием Уолша-Адамара. [6]
Матрицей Адамара называется ортогональная квадратная матрица, элементами которой являются действительные числа 1 и -1. Простейшей матрицей Адамара является матрица порядка два:
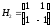 .
.
Для построения
матрицы Адамара порядка
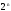 используется матрица
используется матрица и теорема: если
и теорема: если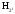 - матрица Адамара порядка
- матрица Адамара порядка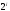 ,
то
,
то
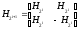 является матрицей
Адамара порядка
является матрицей
Адамара порядка
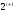 .
.
Используя матрицу Адамара, запишем преобразования (15) и (16) в матричной форме:
|
B
=
|
(15) |
|
S
=
|
(16)
|
где B = [B(0), B(1), …,B(N-1)] – вектор коэффициентов преобразования Уолша-Адамара;
S = [S(0), S(1), …,S(N-1)] – вектор отсчетов входного сигнала;
H - матрица Адамара порядка N. [6]
Вычисление по
формулам (13), (14) требует N(N-1)
операций. Существуют быстрые алгоритмы
(быстрые преобразования Адамара (БПУА)),
которые требуют только N
log N
операций. Их сущность заключается в
разбиении матрицы Адамара в произведение
слабозаполненных матриц. Процесс
умножения на матрицу Адамара заключается
в последовательном умножении на
слабозаполненные матрицы.
N
операций. Их сущность заключается в
разбиении матрицы Адамара в произведение
слабозаполненных матриц. Процесс
умножения на матрицу Адамара заключается
в последовательном умножении на
слабозаполненные матрицы.
Вывод: Вычислительные
преимущества БПУА по сравнению ДПУА
следующие: ДПУА требует N(N-1)
операций, а БПУА требуют только N
log N
операций. Таким образом, вычислительная
экономия составляет N(N-1)
/ N
log
N
операций. Таким образом, вычислительная
экономия составляет N(N-1)
/ N
log N.
Например, если N=1024,
то выигрыш составит 1024(1024-1)/1024 log
N.
Например, если N=1024,
то выигрыш составит 1024(1024-1)/1024 log 1024=102,3
раза. [5]
1024=102,3
раза. [5]
2.4.4. Дискретное косинусное преобразование
Дискретное косинусное преобразование непосредственно связано с ДПФ. Недостаток ДПФ заключается в том, что спектральные коэффициенты носят комплексный характер. Однако можно осуществить такое преобразование множества отсчетов сигнала Х(n), в котором используется только реальная часть ядра преобразования ДПФ, т.е. только члены, связанные с соs. Используя запись ДПФ, получаем выражения для прямого (17) и обратного (18) ДКП:
|
C(k)
=
|
(17)
|
|
|
(18) |
где с(k)
=
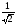 дляk
дляk 0,
0,
1 для
k

Матричная форма записи ДКП имеет вид:
Прямое одномерное ДКП
|
|
(19)
|
где [С(k)]
– вектор- столбец спектральных
коэффициентов ДКП размером (N 1);
1);
|
|
(20) |
где [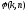 ]
матрица дискретного множества функций
ДКП размером (N
]
матрица дискретного множества функций
ДКП размером (N N);
N);
[X(n)]
– вектор-столбец отсчетов сигнала
размером (N 1).
[6]
1).
[6]
Обратное одномерное ДКП
|
|
(21) |
Прямое ДКП
двухмерного фрагмента изображения
размером (N N)
запишется как
N)
запишется как
|
|
(22)
|
где [C(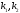 )]
– матрица спектральных коэффициентов
ДКП размером (N
)]
– матрица спектральных коэффициентов
ДКП размером (N N);
N);
[X(n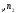 )]
– сигнальная матрица размером (N
)]
– сигнальная матрица размером (N N);
N);
[ ]
– матрица ДКП размером (N
]
– матрица ДКП размером (N N)
в соответствии с формулой (19):
N)
в соответствии с формулой (19):
|
|
23)
|
где
 - матрица ДКП размером (N
- матрица ДКП размером (N N):
N):
|
|
(24)
|
Прямое двухмерное преобразование ДКП в матричной форме имеет вид:
|
[C( |
(25)
|
Обратное преобразование в матричной форме записывается как
|
|
(26) |
2.4.5. Дискретное преобразование Хартли
К линейному ортогональному преобразованию относится и преобразование Хартли (ПХ). Это преобразование связано с преобразованием Фурье, результат выражается действительными числами, но в отличии от косинусного прямое и обратное преобразования Хартли совпадают, что может обеспечить экономию аппаратных средств. [1]
Прямое и обратное одномерное ПХ записывается следующим образом:
|
|
(27) |
|
|
(28) |
где cas( )
=cos(
)
=cos(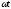 )+sin(
)+sin(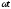 );
);
 - круговая частота;
- круговая частота;
t – время.
Дискретное одномерное преобразование Хартли (ДПХ) имеет вид
|
|
(29)
|
где
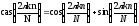 .
.
Выражение (29) задает
коэффициенты разложения (коэффициенты
Хартли) некоторой действительной функции
g(n)
по дискретным функциям
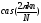 ,
причемg(n)
задана на дискретном множестве аргументов
n
,
причемg(n)
задана на дискретном множестве аргументов
n {0,1,…,N-1}.
{0,1,…,N-1}.
Используя свойство ортогональности функций, можно получить выражение для обратного одномерного дискретного преобразования Хартли (ОДПХ):
|
g(n)= |
(30) |
Матричная форма записи одномерного прямого ДПХ имеет вид
|
[G(k)]=[v(k,n)][g(n)],
k,
n |
(31)
|
где [v(k,n)]=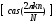 - матрица дискретного множества
ортогональных функций ДПХ размером
(N
- матрица дискретного множества
ортогональных функций ДПХ размером
(N N);
N);
[G(k)]
– вектор-столбец спектральных
коэффициентов ДПХ размером (N 1);
1);
[g(n)] – вектор-столбец дискретных значений (отсчетов) сигнала.
Обратное одномерное ДПХ в матричной форме записи представляется как:
|
[g(n)]= |
(32)
|
Прямое ДПХ
двухмерного фрагмента изображения
размером (N N)
запишется в виде
N)
запишется в виде
|
[G( |
(33)
|
где [g(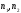 )]
– сигнальная матрица размером (N
)]
– сигнальная матрица размером (N N);
N);
[G(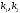 )]
– матрица спектральных коэффициентов
ДПХ размером (N
)]
– матрица спектральных коэффициентов
ДПХ размером (N N);
N);
[v(k,n)]
– квадратная матрица ДПХ размером
(N N):
N):
|
|
(34) |
Двухмерное обратное преобразование Хартли записывается в виде
|
[g( |
(35) |
Отметим, что матрицы
преобразований прямого и обратного ДПХ
идентичны, так как [v(k,n)]=[v(k,n)] [10].
[10].
Спектральный метод
Применение ДПФ для сравнения матриц (фрагментов изображений):
а) Строим матрицу прямого ДПФ
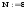
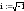
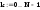
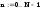
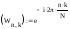

Транспонированное ядро ДПФ:

При
этом допускают все известные способы
распараллеливания векторно-матричных
операций. Если пользоваться обычным
правилом умножения матрицы на вектор,
то вычисления векторов x
и X
требуют
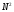 операций комплексного умножения иN(N-1)
операций комплексного сложения.
операций комплексного умножения иN(N-1)
операций комплексного сложения.
2. Быстрое
преобразование Фурье включает набор
эффективных алгоритмов, предназначенных
для вычисления ДПФ. Идея БПФ по своей
природе заключается в следующем. Величина
N,
определяющая длину входной
последовательности отсчетов, раскладывается
на сомножители, затем вычисляются
отдельные ДПФ меньших длин, чем N,
из которых потом формируется выходная
последовательность. Происходит так
называемое расщепление исходного
алгоритма на комбинацию подобных
алгоритмов меньшего размера. БПФ содержит
число мультипликативных операций
(операций комплексного умножения)
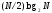 ,
число аддитивных операций (операций
комплексного сложения)
,
число аддитивных операций (операций
комплексного сложения)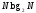 .
[4]
.
[4]
Вывод: Вычислительные
преимущества БПФ по сравнению ДПФ
следующие: БПФ содержит
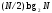 операций комплексного умножения в
отличие от
операций комплексного умножения в
отличие от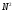 при ДПФ, таким образом, вычислительная
экономия составляет
при ДПФ, таким образом, вычислительная
экономия составляет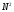 /
/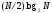 .
Например, еслиN=1024,
то экономия составляет 204,8 раза. БПФ
содержит
.
Например, еслиN=1024,
то экономия составляет 204,8 раза. БПФ
содержит
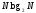 операций комплексного сложения в отличие
отN(N-1)
при ДПФ таким образом, вычислительная
экономия составляет N(N-1)
/
операций комплексного сложения в отличие
отN(N-1)
при ДПФ таким образом, вычислительная
экономия составляет N(N-1)
/
 .
Например, еслиN=1024,
то экономия составляет 102,3 раза.
.
Например, еслиN=1024,
то экономия составляет 102,3 раза.

 ,h=0,1,2,…,N-1,
,h=0,1,2,…,N-1,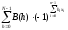 ,h=0,1,2,…,N-1,
,h=0,1,2,…,N-1,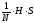 ,
,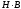 ,
,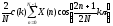 ,k
,k ,
,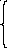 X(n)
=
X(n)
=
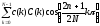 ,n
,n
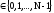 ,
,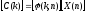 ,
k,
n
,
k,
n {0,1,…,N-1},
{0,1,…,N-1},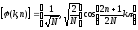 ,
n
,
n {0,1,…,N-1},
k
{0,1,…,N-1},
k {1,2,…,N-1},
{1,2,…,N-1},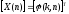 [C(k)],
k,n
[C(k)],
k,n {0,1,…,N-1},
{0,1,…,N-1},
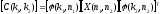 ,
,
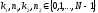 ,
,
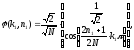
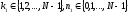 ,
,
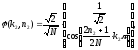
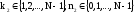 ;
;
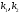 )]
=
)]
=
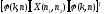 .
.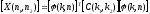 .
.
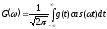 ,
,
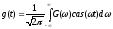 ,
,
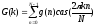 ,
k
,
k {0,1,…,N-1},
{0,1,…,N-1},
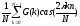 ,
n
,
n {0,1,…,N-1},
{0,1,…,N-1},
 {0,1,…,N-1},
{0,1,…,N-1},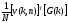 ,
k, n
,
k, n {0,1,…,N-1},
{0,1,…,N-1},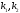 )]
)]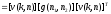 ,
,
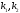 ,
,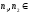 {0,1,…,N-1},
{0,1,…,N-1},
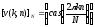 ,
k, n
,
k, n {0,1,…,N-1},
{0,1,…,N-1},
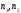 )]=
)]=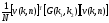 .
.