Отсюда можно гарантировать q(τ) <1 при τ (0,γ2). В частности, при

γ	0	≤ϕ (x)≤	1−γ	<1	.
τ = 1 справедлива оценка		′	α

Метод имеет линейную скорость сходимости.

Метод простых итераций и почти все другие итерационные методы имеют важное достоинство: в них не накапливаются ошибки вычислений. Ошибка вычислений эквивалентна некоторому ухудшению очередного приближения. Но это отразится только на числе итераций, а не на точности окончательного результата. Подобные методы устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости.

6.5. Метод Ньютона

Этот метод называется также методом касательных или методом линеаризации. Если xk есть некоторое приближение к корню ξ , а f (x)

имеет непрерывную производную, то уравнение (6.1) можно преобразовать следующим образом:

0= f (ξ)= f [xk +(ξ−xk )]= f (xk )+(ξ−xk ) f '(θ).

Приближённо заменяя f ′(θ) на значение в известной точке xk , получим итерационный процесс Ньютона, который определяется линейным

уравнением

f (x )+ f (x )(x

−x )=0

k

′

k

k +1

k

или в явном виде формулой

f (xk)

xk +1=xk −

.

(6.11)

′

k

y

f(x)

f (x )

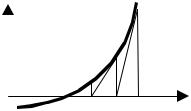
Геометрически этот процесс означает

замену

на

каждой

итерации

графика

x

x

y = f (x) касательной к нему (рис. 6.5).

x2

x1 x0

(xk) к

Интуитивно ясно, что сходимость

ξ

будет тем быстрее, чем ближе

Рис. 6.5 Итерации метода

функция f (x) к линейной и чем круче ее

Ньютона

график

пересекает

ось

абсцисс;

так что

имеет смысл потребовать от f (x) , чтобы по модулю вторая ее производная была ограничена сверху, а первая снизу. Справедлива следующая теорема: Теорема 1: Пусть функция f (x) удовлетворяет условиям

| f ′(x)|≥α>0,

146

| f	′′	x [a,b]
	(x)|≤β<∞,

тогда, если члены последовательности (xk) , определенные методом Ньютона (6.11), при любом фиксированном k N0 принадлежат отрезку [a,b] и эта последовательность сходится на [a,b] к корню ξ уравнения (6.1), то справедливы неравенства ( k N0 )

|ξ−xk +1|≤	β	|ξ−xk|2	(6.12)
	2α
|ξ−xk +1|≤	β	|xk +1−xk|2	(6.13)
	2α

Первое из этих неравенств позволяет считать (6.11) методом второго порядка, а второе являясь апостериорной оценкой погрешности и может служить в качестве критерия прекращения процесса вычислений.

Метод

Ньютона

можно рассматривать

как

частный

случай метода

простых итераций, если положить

ϕ(x)

= x −

f (x)

.

f

′

′′

(x)

ϕ (x) =1−

f (x) f

(x)

Тогда

′

.

(6.14)

′

2

ξ

( f (x))

Если

есть

р-кратный

корень

уравнения,

то

вблизи

него

f (x)≈a(x−ξ) p;

отсюда

нетрудно

получить

ϕ '(ξ) = ( p −1) / p,

т.е.

0 ≤ ϕ '(ξ) <1.

Для

простого

корня р =

1

и

ϕ '(ξ) = 0.

Используя ранее

полученные результаты, можно сформулировать следующие условия сходимости итераций. Если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся; скорость сходимости велика для простого корня и соответствует скорости геометрической прогрессии для кратного корня. При произвольном нулевом приближении

итерации сходятся, если всюду		f (x) f	′′		<( f	′	2 ; в противном случае
			(x)			(x))

сходимость будет не при любом нулевом приближении, а только в некоторой окрестности корня.

Сходимость вблизи любого корня монотонна, что легко видеть из рис.6.5; но вдали от корня возможна немонотонность итераций. Отметим, что рис.6.5 указывает ещё на одно достаточное условие сходимости итераций. Пусть f"(x) ≥ 0 справа от корня на отрезке [ξ, a]; если х0 выбрано также справа от корня на этом отрезке, то итерации сходятся, причём монотонно. То же будет, если f"(x) ≤ 0 слева от корня на отрезке [b, ξ], и на этом же отрезке выбрано нулевое приближение. Таким образом, итерации сходятся к корню с той стороны, с которой f (x) f ′′(x) >0 и справедлива следующая теорема:

147

Теорема 2: Пусть на отрезке [a,b] функция f (x) имеет первую и вторую производные постоянного знака и пусть f (a) f (b)<0 . Тогда, если точка x0

выбрана на [a,b] так, что

f (x0) f ′′(x0)>0 ,

то начатая с неё последовательность ( xk ), определяемая методом Ньютона (6.11), монотонно сходится к корню ξ (a,b) уравнения (6.1).

Оценим скорость сходимости вблизи простого корня. По определению простых итераций ξ −xk =ϕ(ξ) −ϕ(xk−1) . Разлагая правую часть по

формуле Тейлора и учитывая равенство ϕ′(ξ) = 0, получим

xk −ξ = 12 (xk−1 −ξ)2ϕ"(θ), θ (xk−1, ξ),

т.е. погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Например, если (k −1) -я итерация

давала 3 верных знака, то k -я даст примерно 6 верных знаков, а (k +1) -я –

примерно 12 знаков. Это иллюстрирует быструю сходимость вблизи корня. Разумеется, вдали от корня подобные соображения неприменимы.

Если вычисляется корень высокой кратности, то f'(x) в знаменателе формулы становится малой величиной вблизи корня. Чтобы не было потери точности, отношение f (x)/ f ′(x) нужно вычислять достаточно аккуратно. К

остальным погрешностям расчёта метод Ньютона хорошо устойчив.

Для отыскания корней произвольной дифференцируемой функции чаще всего применяют метод Ньютона, особенно если известны разумные начальные приближения для корней.

Модифицированный метод Ньютона применяют,

избежать многократного вычисления производной:

xk +1=xk	−	f (xk )		,	f	′	.
			′
		f				(x0)≠0
			(x0)

Метод имеет линейную скорость сходимости.

6.6. Метод секущих

если хотят

(6.15)

В методе Ньютона требуется вычислять производную функции, что не всегда удобно. Можно заменить производную первой разделённой разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. Тогда получим

x	=x	−(xk −xk −1) f (xk ) .				(6.16)
k +1	k		f	(xk )− f (xk −1)

148

Для начала процесса надо задать х0 и					х1 (рис. 6.6). Такие процессы, где для
				вычисления очередного приближения нужно
y		f(x)		знать	два	предыдущих,	называют
				двухшаговыми.
				Эти, казалось бы, небольшие изменения
	x		x	сильно влияют на характер итераций.
				Например, сходимость итераций может быть
	x3 x2 x1	x0
				немонотонной не только вдали от корня, но и
Рис. 6.6 Итерации методау секущих				в малой окрестности корня.
				Скорость сходимости можно оценить,

разлагая все функции в по формуле Тейлора с центром ξ Получим с точностью до бесконечно малых более высокого порядка

xk +1−ξ=a (xk −ξ)(xk −1−ξ), a=	f "(ξ)		(6.17)
		.
	2 f '(ξ)

Решение этого рекуррентного соотношения естественно искать в виде

степенной функции x	−ξ =aα (x − x)β	. Подставляя эту форму в
k +1	k
соотношение, получим

αβ = 1, β2 - β - 1 = 0.

Только положительный корень β квадратного уравнения соответствует убыванию ошибки, т.е. сходящемуся процессу. Следовательно, в методе секущих

x			−ξ	=a1/ β (x	−ξ)β ,
k +1				k
β	= 1	( 5		+1) ≈1,62; 1/ β ≈0,62,
	2

в то время как в методе Ньютона ошибка убывает быстрее (соответствуя β = 2). Но в методе Ньютона на каждой итерации нужно вычислять и функцию, и производную, а в методе секущих, – только функцию. Поэтому при одинаковом объёме вычислений в методе секущих можно сделать вдвое больше итераций и получить более высокую точность.

Взнаменателе формулы стоит разность значений функции. (Заметим, что приводить формулу к общему знаменателю не следует: увеличится потеря точности в расчётах.). Вдали от корня это несущественно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, что приводит к увеличению погрешности, начиная с некоторой итерации. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение невелико,

адля кратных может быть существенным.

Втакой ситуации применяют так называемый приём Гарвика:

выбирают не очень малое ε и ведут итерации до выполнения условия

149

f (x)

|xn + 1 – xn| < ε и затем продолжают расчёт до тех пор, пока величины

|xn+ 1 – xn| убывают. Первое же возрастание обычно означает начало увеличения погрешности, тогда расчёт прекращают и последнюю итерацию не используют.

6.7. Метод парабол

Если в методе Ньютона вместо производной вычислять разность первого порядка, то это можно рассматривать как замену функции

интерполяционным многочленом первой степени, построенным по узлам хn, хn-1. Но по трем последним итерациям можно построить интерполяционный многочлен второй степени, т.е. заменить график функции f (x) параболой.

Если воспользуемся интерполяционным многочленом Ньютона в конце таблицы, то приравняв его к нулю, получим квадратное уравнение:

az2 +bz +c =0,	(6.18)
где
z=x−xn, a= f (xn,xn−1, xn−2), b=a(x−xn)+F(xn,xn−1),	c=F(xn).

Тогда, решив уравнение, выбирают меньший по модулю корень, который будет определять новое приближение: х n+1= хn + z.

Очевидно, что для начала расчетов надо определить первые три приближения х0, х2 и х3. Обычно задают любые три числа из отрезка, на

котором ищется корень, но можно определить эти значения и иначе.

Метод парабол относится к трехшаговым методам. По сравнению с ранее изученными он сходится гораздо медленнее, но имеет следующее достоинство: даже если все предыдущие приближения действительны, этот метод может привести к комплексным числам. Во всех же остальных методах для сходимости к комплексному корню требуется задание комплексного начального приближения. Кроме того, метод парабол исключительно эффективен для нахождения всех корней многочлена высокой степени. Интересно заметить, что если f (x) – некоторый многочлен высокой степени,

то, хотя сходимость метода не доказана [Касаткин, 1978], при произвольном начальном приближении, на практике итерации всегда сходятся к какомулибо корню. По теореме Горнера для алгебраического многочлена частное f (x)/(x −xn) будет тоже многочленом, но меньшей степени. Поэтому,

последовательно удаляя найденные корни, можно найти все корни многочлена.

6.8. Комбинированный метод (хорд и касательных)

Методы хорд и касательных дают приближения корня с разных сторон. Поэтому их часто применяют в сочетании. Комбинации методов могут быть

150

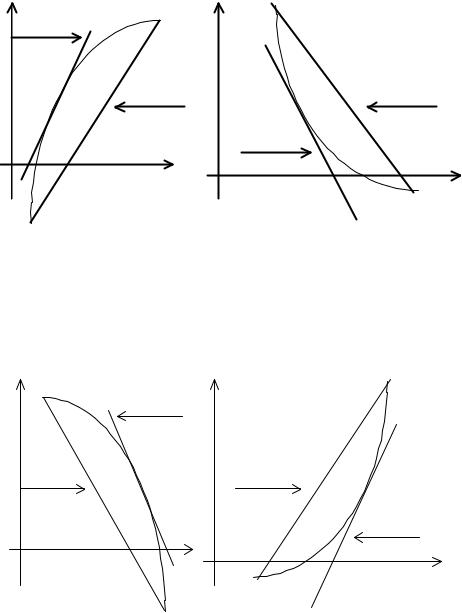
различны, но во всех случаях уточнение корня идет быстрее. Рассмотрим несколько вариантов расчетных схем комбинированного метода.

Метод касат.
Метод хорд	Метод хорд
	Метод касат.

Рис. 6.7 Графическая интерпретация комбинированного метода при f '(х)f "(х) > 0

Если	f (x) f	(x)	>	0	(рис. 6.7), то метод хорд дает приближение корня с
	′	′′
недостатком,		а метод касательных – с избытком. Если же				f (x) f	(x)	<	0
						′	′′

(рис. 6.8), то, наоборот, метод хорд дает приближение корня с избытком, а касательных – с недостатком.

	Методкасат.
	Методхорд
Методхорд	Методкасат.
Рис. 6.8 Графическая интерпретация комбинированного

метода при f '(х)f "(х) < 0

Однако во всех случаях истинный корень ξ заключен между промежуточными корнями, получающимися по методу хорд и методу касательных, т.е. выполняется неравенство

а < х < ξ Х< < b,

где х – значение корня с недостатком, а Х – с избытком.

Из этих соображений складывается следующая схема вычислений: в

первом случае, когда выполняется условие	f	(x) f	(x)	>	0	, то
		′	′′

151

последовательность {хi} (слева) образуется по методу хорд, а последовательность {Хi} (справа) образуется по методу касательных:

xi = xi−1 −

f (xi−1 ) ( X i−1 − xi−1 )

;

(6.19)

f ( X

i−1

) − f (x

)

i−1

X i = X i−1

−

f ( X i−1 )

.

f ′( X i−1 )

Во втором случае, когда

f

′

′′

<

0

,

слева лежит приближенное

(x) f (x)

значение корня, найденное по методу касательных, а справа – по методу хорд. При этом расчетные формулы будут несколько иные:

xi

= xi−1

−

f

( xi−1 )

;

(6.20)

f

′(xi−1 )

X i =

X i−1

−

f ( X i−1 ) ( xi−1

− X i−1 )

.

f ( xi−1 ) − f

( X i−1 )

Другая вычислительная схема этого же метода дает более быструю

сходимость:

xi = xi−1 −

f (xi−1 ) ( X i−1

− xi−1 )

;

(6.21)

f ( X i−1 ) − f (xi−1 )

X i = xi −

f (xi )

.

f ′( xi

)

Для начала процесса в этом случае полагают x0 = a, X0 = b. За

приближенное

значение после окончания вычислений при любой из рассмотренных схем принимают среднее между Хn и хn: ξ ~ 1/2 (Хn + хn).

6.9. Методы ускорения сходимости

В применении к некоторым уравнениям рассмотренные итерационные методы сходятся довольно медленно. В таких случаях особое значение приобретают способы, позволяющие оптимизировать итерационный процесс путем ускорения сходимости метода итераций. Один из наиболее часто употребляющихся алгоритмов – метод Эйткена ускорения сходимости.

Главным является требование линейной сходимости основного итерационного метода. В случае методов, имеющих более высокую скорость сходимости, ускорение по Эйткену неэффективно. Метод состоит в том, что

после вычисления xn, xn+1 и xn+2 производится пересчет по формуле

yn+1 = xn+2	−	(xn+2		− xn+1)2
					(6.22)
		xn+2	−
				2xn+1 + xn

и значение yn+1 принимается за новое приближение. Оно дает лучшее приближение к корню, чем очередная итерация xn+2. На практике не обязательно проводить пересчет на каждой итерации. Обычно он

152

осуществляется циклически, т.е. через определенное число основных итераций.

С помощью метода Эйткена на основе известных итерационных методов получены новые, обладающие более высокой сходимостью.

Метод Вегстейна – улучшенный по Эйткену метод простой итерации;

– записан в виде, позволяющем проверять целесообразность пересчета:

y

n

= x

n+1

−

xn+1 − xn

,

r

=

xn − xn−1

.

(6.23)

rn

−1

n

xn+1

− xn

Если rn почти постоянны, то использование в качестве очередного

приближения yn+1 сильно ускорит сходимость. Итерации прекращают, если выполняется

(xn+2 − xn+1)2	< ε.
xn+2 − 2xn+1 + xn

Метод Стеффенсена имеет квадратичную сходимость, – более быструю, чем исходный метод релаксации:

	xn+1	= xn −	f 2	(xn )	.	(6.24)
			f (xn ) − f (xn − f (xn ))

153