METODA

x2		=	x
			2
.............. ,
x		=	xn
	n
где xk	есть		определитель, получается из	заменой к-го столбца	столбцом
свободных членов. Объединяя их с (1.5), получаем систему
x1		=	x
			1		(1.6)
.............. .
x		=	xn
	n

Система (1.6) является следствием системы (1.4). Таким образом, мы показали, что если система (1.4) имеет решение, то это решение будет и решением системы (1.6).

Если ≠ 0 то из (1.6) получаем

x =	xk	k =1, 2,..., n.	(1.7)
k
Непосредственный подставной этих значений в систему (1.4) можно
убедиться, что они действительно являются ее решением.			Формулы (1.7)
называются формулами Крамера.

Анализируя систему (1.6), мы можем сделать следующие выводы.

1)	Если ≠ 0 , то система (1.4) имеет единственное решение, которое может
быть вычислено по формулам Крамера.
2)	Если	=0 , но хотя бы один из вспомогательных определителей x	не
		k
равен нулю, то система (1.6), а значит и система (1.4), решений не имеет.
3)	Если	= x1 =K= xn = 0 , то случай называется особым. В этом случае

нужно дополнительное исследование. В дальнейшем мы покажем, что в данном случае система либо имеет бесконечно много решений, либо их не имеет вовсе.

Если все свободные члены в системе (1.4) равны нулю, т.е.

b1 = b2 = …= bn = 0, то система называется однородной. Очевидно, однородная система всегда имеет нулевое решение х1 =х2 = …=хn = 0. Из выше приведенных рассуждений вытекает, что это решение будет единственным тогда и только тогда, когда ≠ 0 .

2.ВЕКТОРЫ В ПРОСТРАНСТВЕ

2.1.Определение вектора. Линейные операции над векторами

11

Вектором будем называться направленный отрезок или, что тоже самое,
упорядоченную пару точек. Обозначают вектор						ur	uur
						a	или AB .
Вектор,	rу которого начало и конец совпадают, называется нулевым и
обозначается	0 .	uur		uuuur
Длина вектора обозначается			или		.
		a		AB

Векторы называются коллинеарными, если они параллельны некоторой прямой. Если векторы параллельны некоторой плоскости, то их называют компланарными.

Определение 1. Векторы называются равными, если они равны по длине, коллинеарны и одинаково направлены.

Из данного определения вытекает, что векторы можно свободно перемещать

в пространстве.

ur

Произведением вектора

a на число α называется вектор b такой, что

1)

br

=

α

ar

,

2) b коллинеаренra ,

0,

и противоположно,

3) векторы a и b направлены одинаково, если α >

если α <0.

Вектор (-1) a называется противоположным вектору a

и обозначается

- a .

Суммой векторов a и

b называется вектор

( a +b ),

который строится по

правилу треугольника или параллелограмма

Разностью векторов a и b называется сумма

a и -b .

a+b	b	b
		a+b

a	a
Геометрически это:

12

b b–a

a

Линейные операции над векторами обладают следующими свойствами, вытекающимиr непосредственноr из их определения.

1) α (βa )= (αβ )a,

r r r r

2)ar+br=br+a, r r r

3)a+r(b+rc )=(ra+br)+c,

4)α(a+br)=αra+αrb,

5)(α+β )a = aα + aβ.

	Кроме того, справедливо свойство
	6)	если	r	r	то	для	любого	вектора b	коллинеарного		a существует
			a	≠ 0,
единственное число λ такое, что b = λ a .
				2.2.Линейная зависимость векторов. Базис
	Векторы		ur	uur	uru
			a1, a2 ,K, an называются линейно зависимыми, если существуют числа
λ1	,K, λk не все равные нулю такие, что
	ur	uur			uur	r
	λ1 a1	+λ2 a2	+urKuur+λk anuru=			0 .			если		(2.1)
	Векторы		a1, a2 ,K, an			линейно независимые,				данное равенство может
иметь место только при λ1 = λ2							=K= λk	= 0 .
	Выражение				ur	uur	uur	называется		линейной	комбинацией
					λ1 a1 +λ2 a2 +K+λk an
	ur uur		uur				что если несколько векторов линейно зависимы, то
векторовa1, a2 ,K, an . Очевидно,

хотя бы один из них можно представить в виде линейной комбинации остальных. Справедливо и обратное: если один из векторов представлен в виде комбинации остальных, то все эти векторы линейно зависимы.

Пример. Любые два коллинеарных вектора линейно зависимы и любые два некаллиниарные вектора линейно независимы.

13

ar br br = λar br −λar = 0,

r

r

r

λ

r

r r

λ b

−λ a =

0, λ ≠ 0,

b = −

1

a a b.

1

2

1

λ2

Можно также показать,

тройка компланарных векторов линейно зависима, а

три некомпланарных вектора всегда линейно не зависимы.

Теорема. Максимальное число линейно независимых векторов на плоскости

равно двум, а в пространстве – трем.

Базисом на плоскости называют два любых линейно независимых вектора.

Таким образом, два неколлинеарных вектора образуют на плоскости базис.

uur

rи

r

Пусть

ra

b - образуют базис на плоскости, а c - вектор плоскости. Т.к.

векторы

a ,

b ,

c

r

линейно зависимы, то c можно представить в виде комбинации

uur

r

r

r

a

и b , т.е.

c = λ1 a

+λ2 b .

ur

r

Тогда говорят,

что вектор

разложен по базису

и

λ2

c

a

b , а числа λ1,

называют его координатами или компонентами в данном базисе. Данный факт

записывается следующим образом: c =( λ1, λ2 ).

Разложение

вектора

по

базису

единственно.

Действительно,

если

r

r

r

r

r

то

предположить, что вектор c имеет два разложения c = λ1 a +

λ2 b и

c =

μ1 a + μ2 b,

0r = (λ1 −μ1 )ar +(λ2

−μ2 )br,

ur

что в силу линейной независимости

и b

возможно только при

a

λ1 − μ1

= 0

и

λ2 − μ2 =0, т.е. λ1 = μ1

и λ2 = μ2 .

Базисом в пространстве называют тройку линейно независимых векторов.

ur

Как и в случае плоскости вектор

d

однозначно разлагается по векторам базиса

a ,

b ,

r

ur

r

r

r

и он имеет координаты λ1, λ2 , λ3

в данном базисе.

c . Т.е.

d

= λ1 a

+λ2 b +λ3 c

Записывают это d =( λ1, λ2 , λ3 ).

Рассмотрим прямоугольную систему координат в пространстве Оxyz. На

каждойrих осей выберем единичный (т.е. единичной длины) вектор

i

−на Ox,

rj −

на

Oy,

kr − на Oz.

Эти три единичных взаимно перпендикулярных вектора называют ортами.

Т.к. они не компланарны,

то образуют базис – декартов прямоугольный базис.

Любой вектор a в пространстве может быть разложен по данному базису.

r

r

+ ay

r

r

= (ax ; ay ; az )

a = ax i

j

+ az k

или

r

r

r

r

a

= xi

+ y j + zk = (x; y; z).

14

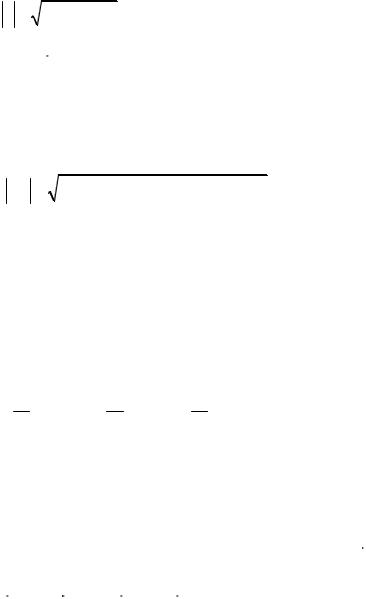
ur

Причем координатами (ax ; ay ; az ) или (x; y; z) будут проекции вектора a на

соответствующие оси координат.

Линейные операции над векторами сводятся к арифметическим операциям

над их координатами.

ar +br = (ax +bx , ay +by , az +bz ),

λar = (λax ,λay ,λaz ).

Зная координаты вектора легко найти его длину r

a = ax2 + ay2 + az2 .

Каждой точке M пространства можно представить в соответствии ее радиусвектор OM . Координаты этого вектора называют координатами точки и записывают М (x; y; z).

Рассмотрим вектор
uuur uuur uuur	− x1	, y2	− y1, z2 − z1 ).
AB = OB −OA = (x2

Отсюда его длина

uuur = − 2 + − 2 + − 2

AB (x2 x1 ) (y2 y1 ) (z2 z1 ) .

Направление вектора в пространстве определяется углами α, β,γ которые вектор составляет с осями координат. Косинусы этих углов называются направляющими косинусами вектора.

Пусть дан вектор

ar = axri +ay

rj +az kr.

uur

на ось Ox

и следовательно, ax =

r

Тогда аx - проекция a

a

cosα.

Аналогично bx

=

br

cos β ,

cx =

cr

cosγ

- проекции на оси Oy,

Oz.

и значит

cosα =

a

ay

cosγ =

a

.

rx

, cos β =

r

,

rz

a

a

a

Если данные равенства возвести в квадрат и сложить,

получим

a2 + a

2 + a2

cos2 α +cos2 β +cos2 γ =

x

y

z

=1.

ar

2

Легко видеть что проекция единичного вектора a на оси координат совпадают с его направляющими косинусами и, следовательно, в случае единичного вектора

a= cosαi + cos β j + cosγ k .

2.3.Деление отрезка в данном отношении

15

Разделить отрезок М1М2 в данном отношении λ > 0 значит найти на данном отрезке точку М такую, что

M1M = λ или M1M = λMM2 . MM2

Пусть M1 (x1

, y1, z1 ),

M2 (x2

, y2 , z2 ) . Найдем координаты точки M (x1, y1, z) . Очевидно

uuuuuur

uuuuur

uuuuur

uuuuur

uuuuur

uuuuur

uuuuuur

M1M

= OM

−OM1,

MM2 = OM2

−OM ,

M1M =

λMM2.

Обозначим

ur

uuuuur

ur

uuuuur

r

uuuuur

Тогда

r1

= OM1,

r2 = OM2 , r

= OM .

uuuuuur

r

ur

ur

r

uuuuuur

следует

из M1M = λMM2

r

−r1

= λ

(r2 −r).

Отсюда

λrr

2 +rur

r

=

r

1+λ

1

или, расписывая покоординатно, получаем

x = λx2 + x1

,

y = λy2 + y1 ,

z = λz2 + z1 .

1+λ

1+λ

1+λ

3.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

Определение.

Скалярным произведением двух векторов a и b называется

число, равное произведению длин этих векторов на косинус угла ϕ между ними. Записывается: ab = ab cosϕ

Физическая интерпретация: точка М движется по прямой. На точку действует постоянно сила F под углом ϕ к направлению перемещения точки.

Тогда работа А силы								F будет равна скалярному произведению векторов силы F	и
							r	urr
перемещению l , т.е.								A = Fl.
Обозначим
Если праb - проекция вектора b на ось вектора a , тогда известно, что
праbr	=				br		cosϕ,
rr	uur						r
ab =	a		праb.
rr	r						ur
ab =	b		пра а.

Т.е. скалярное произведение двух векторов равно длине одного из низ, умноженной на проекцию на него другого вектора.

16

r

rr

rr

ab

ab

праb =

r

,

cosϕ =

r

r

.

a

a

b

Рассмотрим некоторые свойства скалярного произведения.
1)	rr			rr		(свойство коммутативности).
	ab = ba
Это свойство непосредственно вытекает из определния скалярного
произведения.
rr		r		r		rr
ab =		a		b	cosϕ = ba.

2)λ(ab)= (λa)b = a(λb), где λ - скаляр.

Свойство ассоциативности.
r	r r rr	rr
3) (a	+b)c = ac +bc (свойство дистрибутивности).
Дейтвительно
r r r r		r r r	r	r rr rr
(a +b)c = c прс		(a +b)= c (прс a +прсb)= ac +bc.

rr r2 2

4)aa = a = a .

5)Необходимым и достаточным условием ортогональности двух векторов

a и b является равенство нулю их скалярного произведения,
							r	r	rr
					т.е. a b				ab = 0 .
					Доказательство.
					Необходимость. Пусть ar br, значит
							ϕ = π			rr
								cosϕ = 0 ab = 0.
	2									rr	. Тогда
					Достаточность. Пусть ab = 0
	a				b		cosϕ = 0,
отсюда cosϕ = 0 ϕ = π .
										2	r
					6) Если ненулевые векторы
											a и b составляют острый угол, то их скалярное
произведение положительно, если тупой – отрицательно.
r			r Скалярное							произведение	в координатной форме. Пусть две вектора
a,			b определены своими прямоугольными декартовыми координатами
							r			r
							a = (x1, y1, z1 ),			b = (x2 , y2 , z2 ).

Тогда

17

rr

r

r

r

r

r

r

ab = (x1i + y1

j

+ z1 k )(x2 i

+ y2 j + z2 k )=

uur

rr

+ x z

rr

rr

+ y y

r

2

+ y z

rr

+

= x x j2 + x y

2

ji

ik

+ y x ji

2

j

2

jk

1

2

1

1

2

1

2

1

1

rr

rr

+ z z

r

2

,

+z x ki + z y

2

k j

2

k

1

2

1

1

но

rr

rr

rr

rr

rr

r

r

r

rr

=

=

=

i j

= ik

ji = ki

jk

= k j

= 0, i2

j

2 = k2 =1.

Следовательно

abrr = x1x2 + y1 y2 + z1z2 .

4.ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЕ

4.1.Векторное и смешанное произведение

Рассмотрим упорядоченную тройку неколлинеарных векторов ar, buur, cr , которые имеют общее начало. Эта тройка называется правой, если из конца

третьего вектора кратчайший поворот от первого вектора ко второму виден
против часовой стрелки. В противном случае тройка называется левая.
r	r	Определение 1. Векторным произведением векторов a ×br			называется вектор
		r	r	rr
c	= a	×b	(c	= ab ) такой, что
1)	r		r r	r r
	c = a b sinϕ, где ϕ = a b;

r r r

2)c a,b;

3)	r r r
	тройка a,b, c −правая.
	r	r	r
	Пример. i	× j	= k.
	Из определения вытекают геометрические свойства векторного
произведения.				r
	1) Модуль векторного произведения
				a ×b равен площади параллелограмма,
построенного на векторах a и b .					r
	2) Критерий коллинеарности векторов. Векторы					коллинеарны тогда и
					a, b
						r r	r

только тогда, когда их векторное произведение равно нулю, т.е. a ×b = 0 .

Чтобы вывести остальные свойства векторного произведения, удобнее сначала ввести еще одну операцию над векторами – смешанное произведение.

4.2. Смешанное произведение

Определение 2. Смешанным произведением векторов ar, bur, urc называется скалярное произведение вектора a ×br на вектор c .

18

Обозначается смешанное произведение	rr	Таким образом,	по
	abc .
определению
rrur r r r
ab c = (a ×b)c .
Рассмотрим свойства смешанного произведения.
Свойство 1. Смешанное произведение неколлинеарных векторов ar, bur, urc			по

модулю равно объему параллелепипеда, построенного на этих векторах,

приведенных к общему началу. Оно положительно, если тройка ar

, bur,

urc - правая, и

отрицательно, если она – левая.

Доказательство. Очевидно

rrr

r r

r

r

r

r

sinϕ ,

abc

=

a ×b

c

cos Θ

=

a

b

c

cos Θ

r

r

и

ur

r

где φ – угол между a

b,

Θ - угол между a ×b и

c . Но объем V построенного

параллелепипеда равен произведению площади основания S =

ar

br

sinϕ

на высоту

H =

c

cosΘ

V

=

a b c

.

rrr

r

r

r

Знак

смешанного

произведения

=

cos Θ очевидно

совпадает

со

abc

a

×b

c

знаком

cos Θ. Поэтому смешанное произведение положительно,

когда вектор

c

направлен в ту же сторону от плоскости векторов

r

r

r

a и b , что и

a

×b , т.е. когда

тройка векторов

ar, bur, urc

правая.

В противном случае смешанное произведение

отрицательно.

Свойство 2. Смешанное произведение равно нулю тогда

только тогда,

когда его сомножители компланарны.

Доказательство.

rrr

r

r r

r

r

r

r

r

r

cos Θsinϕ .

abc =

0

0 = (a

×b)c

0 =

a

×b

c

cos Θ =

a

b

c

Это возможно в трех случаях.

А) Хоть один из векторов нулевой – тогда все векторы компланарны.

Б)

cos Θ=0, т.е.

вектор

c

ортогонален

r

и следовательно

лежит

в

a ×b

r

r

r

ur

ur

компланарны.

плоскости векторовa и b . Очевидно векторы a,

b,

c

В)

sinϕ =0, т.е.

r

r

r ur ur

a

b ,

тогда очевидно все три вектора a, b,

c лежат в одной

плоскости.

ar, bur, urc

Обратно, пусть векторы

компланарны.

Тогда либо среди них есть

нулевые

в

таком случае

rr

либо

все

не

нулевые, но

лежат в одной

abc = 0 ,

плоскости. Тогда

r r

r

r

r

Θ = 0

a ×b c cos

или a ×b = 0.

В обоих случаях

rrr

abc = 0 .

Из данного свойства следует справедливость следующего утверждения.

19

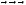
						urur
Критерий компланарности векторов. Для того, чтобы векторы a, b, c
были компланарны,		rr
		необходимо и достаточно чтобы abc = 0.
Замечание. Используя определение правой и левой троек,				можно убедится,
rrr	rrr		с тройкой		urur	(т.е.
что тройки bca;	cab имеют одну и ту же ориентацию				a, b, c
одновременно все правые или все левые). В тоже время тройки				r r r	r r r	r r r
				b, a, c; a,c,b; c,b, a
имеют ориентацию противоположную ориентации тройки			urur
			a, b, c. .
Свойство 3.		rrr r r r r r r
		abc = (a ×b)c = a (b×c).

Доказательство. Если среди векторов есть нулевые, то равенство верно. r(r r) (r r)r rrr rrr

Если нет, то a b×c = b×c a и достаточно показать, что bca = abc . Но в силу свойств 1,2 последнее неравенство очевидно с точностью до знака. И его левая и

его

правая часть

по

абсолютной

величине равны

объему параллелепипеда,

построенного на

r

urur

В случае, если

векторы

компланарны, объем

векторахa,

b, c .

параллелепипеда – нулевой. Но тройки

urur

и

ruu

имеют одинаковую

a, b, c

b, c, a

ориентацию – следовательно,

и знаки тоже совпадают.

Данное свойство служит оправданием записи смешанного произведении в

виде

rrr

abc . Действительно, безразлично, каких два рядом стоящих вектора

умножаются векторно.

Используя свойства смешанного произведения и замечание по ориентации

троек, можно убедится что

rrr

rr

rr

rrr

rrr rrr

abc

= abc =bca = cab = -bac =- acb =- cba

Действительно,

по модулю они все

совпадают

как

объемы одинаковых

параллелепипедов. Первые три имеют одинаковые знаки, т.к. тройки векторов одной ориентации, вторые три – противоположные знаки.

Далее, используя полученное равенство и свойства скалярного произведения

, можно убедиться, что	rrr
r rr r r r rr r

(λa)bc = a (λb)c = ab(λc)= λ(abc),

где λ - скалярный множитель. Также имеют место равенства

ur	uur rr		urrr	uurrr
(a1	+a2 )bc		= a1bc	+ a2 bc,
r r		uur r	rurr	ruurr
a (b1 +b2 )c = ab1 c + ab2 c,
rr	ur	uur	rrr	rrr
ab	(c1	+c2 )	= abc1	+ abc2 .

Полученные равенства используются при вычислении смешанного произведения.

20