
MAT_1
.docx|
1.Матрицы. Основные понятия. Действия над матрицами. Понятие согласованной матрицы.
Действия:
Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.
|
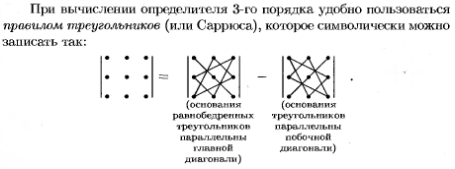
2. Определители и их св-ва. Теорема Лапласа.
Св-ва:
Теорема Лапласа: Определитель кв. матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. |
3.Нормальное ур-ние прямой на плоскости. Расстояние от точки до прямой.
Расстояние
от точки до прямой —
равно длине перпендикуляра, опущенного
из точки на прямую. Если задано уравнение
прямой Ax + By + C = 0, то расстояние от точки
M(Mx, My) до прямой можно найти, используя
следующую формулу:
|
||||||||||||||||||||||||||||||||||||||
|
4.Решение произвольных систем линейных ур-ний методом Крамера, матричным способом, методом Гаусса. Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Если определитель равен 0,то система имеет бесконечное мн-во решений или не имеет вообще.Если определитель не равен 0,то делаем так: Система линейных уравнений: Определители:
Матричный способ(метод решения через обратную матрицу).Определитель должен быть ненулевым. Если матрица А системы линейных уравнений невырожденная, т.е. det(опред.) A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором C = A-1B. Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле X = C, C = A-1B называют матричным способом решения системы, или решением по методу обратной матрицы.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. -Приводим, в результате алгебраических действий к треугольному виду(под главной диагональю нули). -Пишем уравнения(начиная с конечного). |
5.Однородные системы линейныхур-ний. Фундаментальная система решений.
Пусть основная матрица А однородной системы уравнений имеет ранг r, тогда эта система уравнений имеет n–r линейно независимых решений. Совокупность лин. нез. реш. одн. сист. уравнений называется фундаментальной системой решений (ФСР). Общая ФСР может быть записана в виде:
Алгоритм нахождения ФСР:
|
6.Плоскость в пространстве. Все виды ур-ний плоскости. Расстояние от точки до плоскости. Уравнением поверхности S,заданной в прямоугольной декартовой системе координат XYZ, называется уравнение F(x,y,z)=0, которому удовлетворяют координаты x,y,zлюбой точки этой этой поверхности и не удовлетворяют координаты любой точки, не лежащей на ней.
Общее уравнение (1)называется полным ,если все коэффициенты А,В,С и D в нем отличны от нуля. Если хотя бы один из них равен нулю, то уравнение называется неполным.
Нормальное
уравнение плоскости. Расстояние от точки M до плоскости P.
|
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
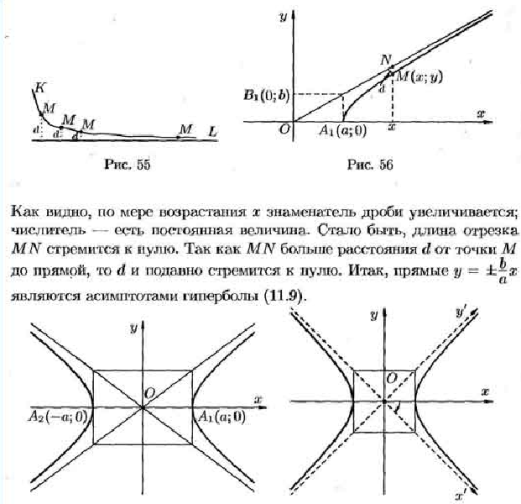
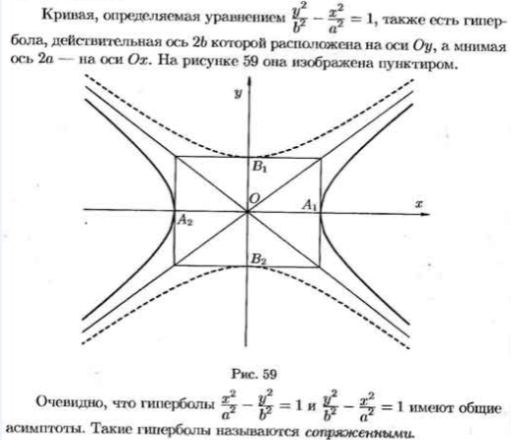
7.Ур-ние элипса, гиперболы, параболы и их основные характеристики.
|
8.Линейная зависимость векторов на плоскости и в пространстве. Взаимное расположение прямых на плоскости. На
плоскости заданы прямые
Если
выполнены условия
Если
выполнены условия
Векторы
Если
скалярное произведение
векторов
Условие
перпендикулярности прямых
|
9. Скалярное, векторное, смешенное произведение векторов и их св-ва.
|
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
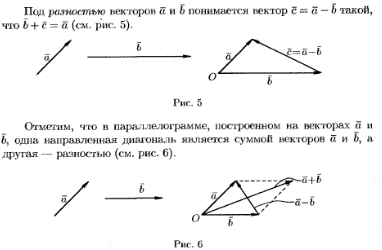
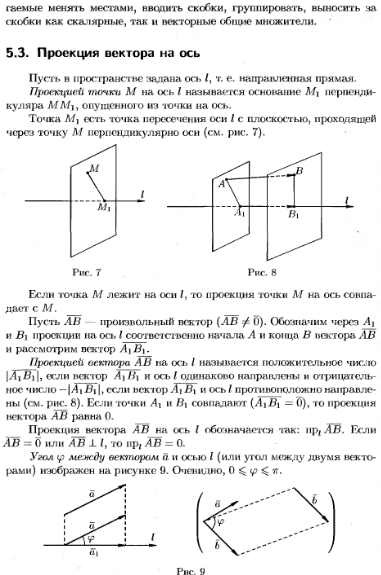
10. Векторы и линейные операции над ними. Проекция вектора. Полярная система координат.
|
11. Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
Пусть
плоскость Q задана уравнением Ах + Ву
+ Cz + D = О, а прямая L уравнениями
Углом
между прямой и плоскостью называется
любой из двух смежных углов, образованных
прямой и ее проекцией на плоскость.
Обозначим через ϕ угол между плоскостью
Q и прямой L, а через ϴ- угол между
векторами n = (А;В;С) и S = (m;n;р).
Тогда cos
ϴ = Если прямая L параллельна плоскости Q, то векторы n и S перпендикулярны, а потому S . n = О, т. е. Аm+Вn+Ср=О является условuеnараллельносmu прямой и плоскости.
Если
прямая L перпендикулярна плоскости
Q, то векторы n и S параллельны . Поэтому
равенства
Прямая и плоскость могут пересекаться .
|
12. Решение производных систем линейных ур-ний. Теорема Кронекера-Капелла.
|
||||||||||||||||||||||||||||||||||||||
|
13. Все виды прямой на плоскости. Взаимное расположение прямых на плоскости Пусть М=(х,у)- произвольная точка прямой l. Тогда вектор М0М=(х-х0,у-у0) перпендикулярен к вектору n(А,В), т.е.(n,М0М)=0 или А(х-х0)+В(у-у0)=0Ax+By+C=0 называется общим уравнением прямой, где С=-Ах0-Ву0 Уравнение прямой с угловым коэффициентом. У=кх+b Каноническое уравнение прямой Пусть М=(х,у)- произвольная точка прямой l. Тогда вектор М0М=(х-х0,у-у0), лежащий на этой прямой, коллинеарен вектору а=(m,n) (х-х0)/m=(y-y0)/n Параметрическое уравнение прямой проходящее через точку М0=(х0,у0)с направляющим вектором а=(m,n) Х=х0+mt , y=y0+nt, t принадлежит R Уравнение прямой, проходящей через две точки М1=(х1,у1),М0=(х0,у0)
На
плоскости заданы прямые
Если
выполнены условия
Если
выполнены условия
Векторы
Если
скалярное произведение
векторов
Условие
перпендикулярности прямых
|
14Деление отрезка в данном соотношении. Декартова система координат.
Если
известны две точки плоскости
Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, –начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел –координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат. Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат
|
15 Взаимное расположение прямых в пространстве. Расстояние между скрещивающимися, параллельными прямыми. Угол между прямыми. Возможны четыре различных случая расположения двух прямых в пространстве: – прямые скрещивающиеся, т.е. не лежат в одной плоскости; – прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку; – прямые параллельные, т.е. лежат в одной плоскости и не пересекаются; – прямые совпадают Найдем расстояние dмежду параллельными прямыми, заданными каноническими уравнениями,
L:
D(L,L1)= Найдем расстояние d между скрещивающимися прямыми, заданными каноническими уравнениями
L2:
где
D=
—
смешанное и векторное произведения
векторов. Как показано выше,
прямые L1 и L2 скрещивающиеся
тогда и только тогда, когда
векторы
L2: вычисляется по формуле
|
||||||||||||||||||||||||||||||||||||||
|
16Линейные операторы и их матрицы в заданном базисе. Преобразование матрицы линейного оператора при переходе к новому базису. Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y . В этих пространствах определены базисы e = {e1, ..., en} и f = {f1, ..., fm}. Пусть A(ei ) = a1i·f1 + a2i·f2 + ...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A ={aij}= {A(ej )i}: Координаты образа y = A(x) и прообраза xСвязаны соотношеннием:y = A· x
|
17 Квадратичные формы. Матрица квадратичной формы, знакоопределенной формы. Критерий знакоопределенности квадратичной формы. Квадратичной
формой от n
переменных х1, х2,…,
Где
Матрица квадратичной формы
Квадратичная
форма Теорема (критерий Сильвестра). Квадратичная форма положительно определена тогда и только тогда, когда все угловые миноры ее матрицы положительны:
Квадратичная
форма отрицательно определена тогда
и только тогда, когда знаки угловых
миноров ее матрицы чередуются, начиная
с минуса: |
18Взаимное расположение плоскостей в пространстве. Уравнение прямой в пространстве. Плоскости в пространстве могут пересекаться или быть параллельными. Условия параллельности и перпендикулярности плоскостей. Пусть две плоскости Р1 и Р2 заданы своими общими уравнениями: Р1: А1х+В1у+С1z+D1=0;
Р2:
А2х+В2у+С2z+D2=0.
P1
перпендикулярно Р2
Р1||P2 Уравнение прямой, проходящей через две различные точки в пространстве Если прямая проходит через две точки A(x1, y1, z1) и B(x2, y2, z2), такие что x1 ≠ x2, y1 ≠ y2 и z1 ≠z2 то уравнение прямой можно найти используя следующую формулу
Параметрическое уравнение прямой в пространстве Параметрические уравнения прямой могут быть записаны следующим образом
где (x0, y0, z0) - координаты точки лежащей на прямой, {l; m; n}- координаты направляющего вектора прямой. Каноническое уравнение прямой в пространстве Если известны координаты точки A(x0, y0, z0) лежащей на прямой и направляющего вектора n = {l;m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Прямая как линия пересечения двух плоскостей Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
при условии, что не имеет место равенство
|
||||||||||||||||||||||||||||||||||||||
|
19Обратная матрица. Ранг матрицы. Элементарные преобразования матрицы..
Обратная
матрица —
такая матрица A−1,
при умножении на которую, исходная
матрица A даёт
в результате единичную
матрицу E: Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю.
Св-ва обратной матрицы:
Рангом системы
строк (столбцов) матрицы A с m строк
и n столбцов
называется максимальное число линейно
независимых строк
(столбцов). Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы.
Обычно ранг матрицы A обозначается Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду Элементарными преобразованиями строк называют:
Аналогично
определяются элементарные
преобразования столбцов.
Элементарные преобразования обратимы.
Обозначение |
20 Линейная зависимость векторов, базис, размерность линейного пространства.
Если
любой вектор системы Система векторов, которая не является линейно зависимой, называется линейно независимой. Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве. Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.
|
21Линейное пространство. Определение, примеры. Линейным (векторным) пространством называется множество объектов, называемых векторами, для которых определена операция сложения и умножения на число(вещественное или комплексное; в зависимости от этого различают вещественные или комплексные векторные пространства),обладающими свойствами:
Примеры
|
||||||||||||||||||||||||||||||||||||||
|
22Поверхности второго порядка.
|
23Собственные векторы и собственные значения линейного оператора. Приведение матрицы линейного оператора к диагональному виду. Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X. Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ. A(x) = λ·x, x ≠0, x ∈ X.
|
|
||||||||||||||||||||||||||||||||||||||
|
24Применение
квадратичной формы к исследованию
кривых В общем случае кривая второго
порядка в базисе
Задача
о приведении кривой
Пусть
– ортонормированные
собственные векторы матрицы A,
соответствующие собственным
значениям
Ортонормированные
векторы
Пусть Тогда ортогональное преобразование:
Приводит
квадратичную форму
Выделив
в этом уравнении полные квадраты,
получим
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||














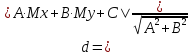
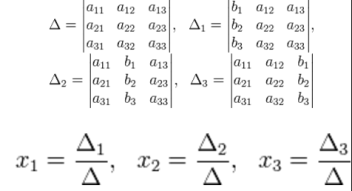
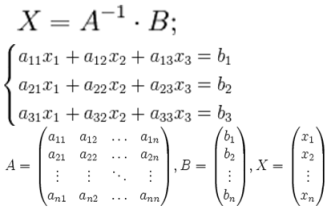



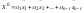
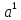 (
(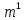 ,
,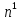 ,
,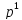 )
и
)
и
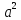 (
(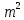 ,
, ,
,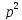 )
и точку M0(x0,y0,z0)
)
и точку M0(x0,y0,z0)
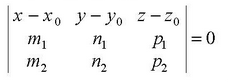 Уравнение
плоскости через три точки.
Пусть плоскость проходит через 3 точки
M1(x1,y1,x1),
M2(x2,y2,z2),
M3(x3,y3,z3),
не лежащие на одной прямой
Уравнение
плоскости через три точки.
Пусть плоскость проходит через 3 точки
M1(x1,y1,x1),
M2(x2,y2,z2),
M3(x3,y3,z3),
не лежащие на одной прямой
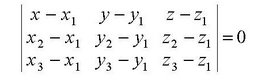
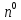 =
(cosα,cosβ,cosγ)(един
вектор нормали к плоскости),
М=(x,y,z)-произвольная
точка плоскости с радиус вектором r=
(x,y,z).
(r,
=
(cosα,cosβ,cosγ)(един
вектор нормали к плоскости),
М=(x,y,z)-произвольная
точка плоскости с радиус вектором r=
(x,y,z).
(r,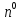 )
-p=0
p>=0
xcosα+ycosβ+zcosγ-p=0
p>=0
)
-p=0
p>=0
xcosα+ycosβ+zcosγ-p=0
p>=0




























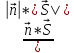 .
sin
ϕ = sin(
.
sin
ϕ = sin(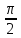 - ϴ) = cos
ϴ. И так как sin ϕ >= О, получаем sin ϕ =
- ϴ) = cos
ϴ. И так как sin ϕ >= О, получаем sin ϕ =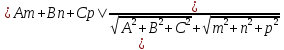 =cos
ϴ
=cos
ϴ
 являются условuямunерендикулярносmu
прямой и плоскости.
являются условuямunерендикулярносmu
прямой и плоскости.


 и L1:
и L1: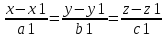 где
где 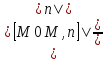
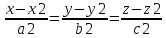 и L1:
и L1:
 =
=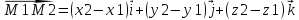
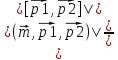 ,где
,где
 Угол
между прямыми определяется как угол
между их направляющими векторами.
Поэтому величина
Угол
между прямыми определяется как угол
между их направляющими векторами.
Поэтому величина 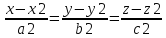 и L1:
и L1: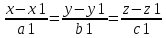

 называется выражение вида
называется выражение вида

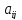 -
действительные числа, называемые
коэффициентами квадратичной формы,
причем считается, что
-
действительные числа, называемые
коэффициентами квадратичной формы,
причем считается, что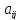 =
=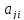

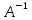 =
=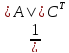

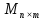 -
матрица n×m
с элементами из R
-
матрица n×m
с элементами из R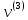 – множество
свободных векторов(пространств,
плоскостей)
– множество
свободных векторов(пространств,
плоскостей)
