1.4. Математичні моделі операцій

У математичних моделях задаються наступні компоненти:

 векторна змінна , що відповідає керованим параметрам;

 векторна змінна , що відповідає некерованим параметрам;

 множина допустимих значень векторної змінної;

 множина допустимих значень векторної змінної;

 цільова функція , що встановлює значення критерію ефективності.

Якщо відоме значення у, то математична модель є детермінованою, інакше – говорять про недетерміновану модель.

Детермінована модель

Нехай приймає значення, відоме нам. Введемо в цьому випадку позначення:

Тоді модель може бути записана в вигляді:

,

(1)

Цей запис означає, що необхідно знайти значення векторної змінної таке, при якому функція досягає мінімуму. Модель (1) називаєтьсязадачею оптимізації.

Недетермінована модель

Якщо є векторною випадковою величиною з відомою імовірнісною мірою, то недетермінована модель називаєтьсястохастичною моделлю.

Якщо операція проводиться неодноразово і має значення середній результат, то математична модель має наступний вигляд:

,

.

Якщо операція проводиться одноразово, або не має значення середній результат (середня температура хворих, що знаходяться в реанімації; результат хірургічної операції для окремо взятого пацієнта; середнє відхилення від директивних термінів виконання), то модель може приймати вигляд:

,

.

Ці задачі називаються задачами стохастичної оптимізації.

Якщо не є випадковою величиною, або це випадкова величина з невідомою імовірнісною мірою, то маємо модель в умовах невизначеності. Така модель може приймати вигляд:

,

.

1.5 Задачі оптимізації - визначення

Надалі розглядатимемо тільки скінченновимірні задачі оптимізації, тобто задачі, допустимі множини X яких лежать в евклідовому просторі .

Точка називаєтьсяточкою глобального мінімумуфункції на множині X або глобальним рішенням задачі (1), якщо

(2)

Точка називаєтьсяточкою локального мінімумуфункції на множині X або локальним розв’язком задачі (1), якщо існує таке, що:

(3)

де 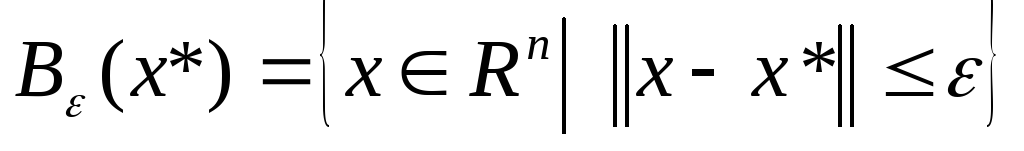- куля радіусаз центром в.

Якщо нерівність в (2) або (3) виконується як строга при , то кажуть, що-точка строгого мінімуму(строгий розв’язок) в глобальному або локальному сенсі відповідно.

Задачу максимізації функції на множинізаписуватимемо у вигляді

,

(4)

Ясно, що задача(4) еквівалентна задачі

.

в тому сенсі, що множини глобальних або локальних строгих або нестрогих розв’язків цих задач відповідно співпадають. Це дозволяє без зусиль переносити твердження для задачі мінімізації на задачу максимізації і навпаки.

Точна нижня грань функції на, тобто величинаназиваєтьсязначеннямзадачі (1).

Можливі три випадки:

a) і при деякому , тобто значення задачі скінчене і досяжне, при цьому;

b) іпри всіх, тобто значення задачі скінчене, але не досягається;

c), тобто значення задачі нескінчене.

У випадку а) задача (1) має глобальний розв’язок, у випадках b) і с) - не має.

Класифікація задач оптимізації

Якщо , то задача (1) називаєтьсязадачею безумовної оптимізації.

Якщо - власна підмножина, то (1) –задача умовної оптимізації.

Якщо визначається так:, а функціїі,є диференційованими, то (1) –задача класичної оптимізаціїі записується у вигляді:

,

.

Під множиною простої структуривбудемо розуміти множини типу:

а) невід’ємного октанта:

б) -мірного паралелепіпеда:

в) -мірної кулі.

Якщо визначається умовами:

де - множина простої структури, то (1) –загальна задача математичного програмуванняі записується у вигляді:

	(5)
	(6)
	(7)
	(8)

Умови (6) називаються обмеженнями – нерівностями. Умови (7) називаються обмеженнями – рівностями. Умови (6) і (7) називаються функціональними обмеженнямизадачі (5)- (8), а умови (8) -прямими обмеженнямизадачі (5)- (8). Розділення обмежень на функціональні і прямі є умовним (вони можуть бути взаємно-зворотніми).

Функція виду називаєтьсяафінною. Якщо, то функціяназиваєтьсялінійною.

Будь-яка афінна функція опукла на будь-якій опуклій множині .

Задача (1) називається задачею опуклої оптимізації, якщо- опукла функція, а множина- опукла множинаⁱ.

Якщо в задачі (5)–(8) – опукла функціяⁱⁱ,- опуклі функції,– афінні функції,- опукла множина, то задача (5)-(8) –загальна задача опуклого програмування.

Якщо в задачі (5)-(8) – лінійна функція,- афінні функції,– невід’ємний октант, то (5)-(8) –задача лінійного програмування.

Якщо в задачі (5)-(8) – квадратична функція, функції- афінні функції,– невід’ємний октант, то (5)-(8)-задача квадратичного програмування.

Якщо в задачі (5)-(8) множина - дискретна, то задача (5)- (8) –загальна задача дискретного програмування.

Якщо в задачі (5)-(8) є адитивними або мультиплікативними, то задача (5)-(8) -задача сепарабельногопрограмування.

Адитивнафункції:

.

Мультиплікативнафункція:

.

iВизначення 1. Множинаназиваєтьсяопуклою, якщо разом з кожними двома точкамивона містить і всі точки вигляду.

Те ж саме геометричною мовою.

Визначення 2. Множинаназиваєтьсяопуклою, якщо з будь-якими двома своїми точками вона містить весь відрізок, кінцями якого служать ці точки.

iiНехай- опукла множина.Функціяопукла намножині, якщо для будь-яких двох точок

якщо , просто кажуть, щоопукла.