2.1. Общий обзор системы.

Наиболее просто количественное рассмотрение нелинейных систем может проведено для двух типов систем, имеющих достаточно большой практический интерес: для систем, близких к консервативным (в первую очередь близких к синусоидальным), а также для систем, поддерживающих разрывные колебания. В данной работе изучается первый тип колебаний.

Мы будем рассматривать, в первую очередь, системы близкие к синусоидальным и достаточно близкие к консервативным.

Уравнениегармонического (синусоидального консервативного ) осциллятора имеет вид :

Уравнение системы, близкой к гармоническому осциллятору имеет вид : (1)

где w – циклическая частота, x – зависимое переменное, - малый безразмерный параметр, который определяет близость нашей системы к консервативной линейной. Данное выражение является упрощением, суть которого заключается в том, что мы считаем функцию f , стоящую в левой части не зависящей от параметра . На практике данное обстоятельство выполняется с достаточно большой степенью точности, поэтому мы и вводим соответствующую идеализацию в нашу модель.

Впрочем, наше, неудобное для численного интегрирования, уравнение второго порядка может быть достаточно легко сведено к системе из двух дифференциальных уравнений первого порядка следующего вида: (2)

Здесь  - безразмерный положительный параметр, который мы предполагаем достаточно малым. Будем также считать, что f(x,y) – полином, а, точнее, наше уравнение имеет вид: (3)

Очевидно, что наше уравнение Ван-дер-Поля – частный случай уравнения (1). Как видно, нелинейность нашего уравнения обуславливается наличием нелинейного множителя перед вторым слагаемым в левой части уравнения. В противном случае, наше уравнение совпадает с хорошо известным уравнением затухающих колебаний. Очевидно также, что близость системы к линейной (консервативной или неконсервативной) определяется параметрами :  (величина, характеризующая диссипативные процессы в системе) и а (малый нелинейный параметр), которые мы и задаем в нашей программе как параметры.

Решение уравнения затухающих колебаний при небольших значениях  хорошо известно, поэтому в процессе решения нелинейного уравнения полезно сравнивать его с соответствующим неконсервативным осциллятором. Его уравнение имеет вид : (4)

Решение данного уравнения : x(t)=A exp(-t) cos(wt+), где величины А и  определяются из начальных условий. На фазовой плоскости данное решение отображается в виде семейства спиралей, имеющих асимптотическую точку в начале координат – рис1.

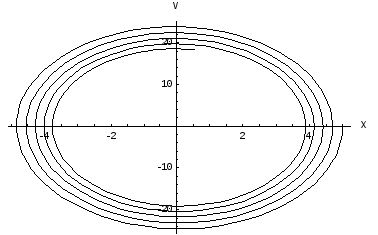
РИС 1.

X(0)=5,V(0)=0.

Однако помимо систем с нормальным положительным “трением” (0), мы можем также (хотя бы формально) рассматривать системы с отрицательным затуханием (0). Решение вновь получившегося уравнения будет иметь принципиально такой же вид, но только не с декрементом, а инкрементом затухания колебаний. Такая система, при анализе её с точки зрения линейного процесса, не будет иметь устойчивых стационарных состояний; она не может остаться в области, близкой к состоянию равновесия, - отклонения в линейной системе должны неизбежно возрастать – рис2.

РИС 2.

X(0)=5,V(0)=0.

С другой стороны, мы рассматривали нашу систему при определённых условиях на значения отклонения системы, при которых она не сильно отклоняется от положения равновесия – в противном случае, наше рассмотрение не является корректным. В то же время, наша система при любой наперед заданной ограниченной области такова, что фазовые траектории стремятся к уходу из этой области. Это значит, что линейная трактовка принципиально не может дать ответа на целый ряд вопросов о поведении системы (например, при прошествии достаточно большого количества времени). Это неизбежно приводит нас к вопросу о возможных нелинейных системах и процессах, аппроксимирующих данный линейный. Одним из таких обобщений и может быть система Ван-дер-Поля.

2. Метод Ван-дер-Поля.

Чтобы исследовать уравнения (3), можно воспользоваться следующим приближённым методом, часто называющимся методом Ван-дер-Поля. Суть его состоит в том, что мы рассматриваем другие, составленные особым образом уравнения. При этом мы подбираем эти уравнения таким образом, чтобы они своим решением аппроксимировали решения нелинейных уравнений (3). При этом, метод Ван-дер-Поля обладает тем важным свойством, что он учитывает специфику нелинейных систем, их характерные черты; вспомогательные уравнения также являются нелинейными, но значительно более простыми.

Пусть задана некоторая фазовая плоскость xy; возьмём на этой плоскости вращающуюся (w) по часовой стрелке прямоугольную систему координат ab. Очевидно, при =0, когда система обращается в простейший гармонический осциллятор, фазовые траектории превращаются в круги с центром в начале координат. Формулы преобразования от переменных x,y к переменным a,b будут иметь следующий вид : (5)

x = a cos t + b sin t, y = - a sin t + b cos t ;

В новых переменных уравнения (5) принимают вид : (6)

Или (7):

Развёртывая правые части в конечные ряды Фурье (считая a и b постоянными), получаем выражения для производных через коэффициенты Фурье. Ограничимся в разложении лишь первым членом, отбросив все остальные : (8)

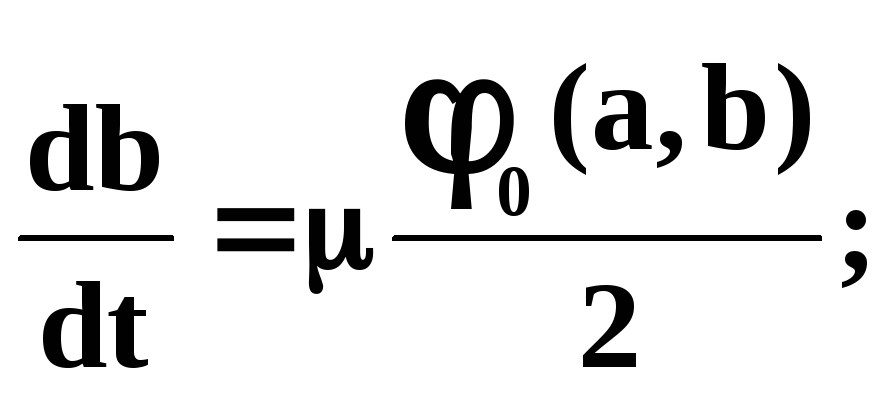
Также как и система (3), данная система является автономной, то есть не зависящей явным образом от времени, что позволяет использовать её для решения проблем на комплексной плоскости. Однако она значительно проще системы Ван-дер-Поля в её исходном виде, при этом при переходе к полярным координатам переменные разделяются. Обозначим: (9)

В таком случае получаем: (10)

где : (11)

В таком виде наша система (3), преобразованная к полярной системе координат, представляется удобной для исследования. Уравнения вполне можно исследовать независимо друг от друга. Начнём с первого из уравнений (10). Качественная картина уравнений такого типа полностью определяется расположением и характером состояний равновесия на соответствующей фазовой прямой.

Координаты этих состояний равновесия – корни уравнения :

Ф(К) = 0,

Состояния равновесия для i-го К будет устойчивым, если:

и неустойчивым, если:

Остальные движения являются либо асимптотическими к состояниям равновесия как при t+, так и при t-, либо асимптотическими к состоянию равновесия для t+ и уходящими в бесконечность для t-.

Второе из уравнений (10) чаще всего ( в частности и в данном конкретном случае) встречается в модификации вида:

В этом случае второе уравнение интегрируется сразу:

Возвращаясь к обычной декартовой системе координат на фазовой плоскости с помощью формул преобразования координат, получим: (12)

Отсюда получаем, что рассматриваемый предельный цикл будет устойчив в своём орбитальном движении по фазовой плоскости в декартовой системе координат, если соответствующие состояния равновесия будут устойчивы, и наоборот. Остальные траектории, представляющие собой на плоскости a,b отрезки прямых, преобразуются на плоскости x,y в спирали, вообще говоря, накручивающиеся на предельные циклы либо при t+, либо при t-.

2. Реализация системы Ван-дер-Поля .

Важнейшим примером применения уравнения Ван-дер-Поля служит процесс автоколебаний в ламповом генераторе с колебательным контуром в цепи сетки. Под автоколебательной системой подразумевают первичный источник колебаний, работающий в режиме самовозбуждения.

Любой автогенератор представляет собой нелинейное устройство, преобразующее энергию питания в энергию колебаний. Независимо от вида и назначения, автогенератор должен иметь: источник питания, усилитель и устройство обратной связи, причём последняя должна быть положительной. Автогенератор, находящийся в стационарном режиме, представляет собой обычный нелинейный усилитель, для возбуждения которого используются колебания, вырабатываемые в самом генераторе; эти колебания берутся из колебательной системы усилителя и подаются на его вход по цепи обратной связи.

В момент запуска в колебательной системе автогенератора возникают свободные колебания, обусловленные включением источников питания, замыканием цепи, флуктуациями и некоторыми другими факторами. Благодаря обратной связи эти первоначальные колебания усиливаются, причём на первом этапе, пока амплитуды малы, усиление является практически линейным, и система может рассматриваться как линейная. Нарастание амплитуд прекращается, когда усиление снижается до уровня, при котором только компенсируется затухание колебаний в нагрузке.

Рассмотрим колебательный контур в режиме генерации колебаний. На основании закона Кирхгофа уравнение, определяющее силу тока в колебательном контуре генерации, можно записать следующим образом: (13)

Пусть анодный ток зависит только от напряжения на сетке, а лампа имеет кубическую характеристику:

Выражение (13) можно переписать в виде:

Вводя безразмерные параметры, а также новую единицу времени можно получить следующее выражение:

Предположив, что параметры – одного порядка малости являются малыми по сравнению с единицей, и вводя малый параметр,  мы (после переобозначения переменных : =x, d/dt=y) приходим к следующей системе (14) :

Очевидно, что данное уравнение (считая =1, а 3=a) идентично нашему уравнению (3), поскольку =0 (не только в случае симметричной нагрузки, но и при небольших отклонениях от неё).

Радиусы предельных циклов (в нулевом приближении) на фазовой плоскости даются уравнением: (15)

В нашем случае первый из безразмерных параметров равен 1, а это значит, что уравнение имеет два принципиально важных корня: (16)

Первый корень соответствует неустойчивой особой точке, так как:

Остальные траектории разбиваются на два типа: траектории, наматывающиеся снаружи на предельный цикл при t и уходящие в бесконечность при t, и на траектории, наматывающиеся изнутри на предельный цикл при t+, и стремящиеся к особой точке при t. Это – картина, характерная для простейшей автоколебательной системы, работающей в мягком режиме.

( В данной реализации рассматривался только «мягкий» режим работы автогенератора).

2. РЕАЛИЗАЦИЯ ЗАДАЧИ. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ.