3.1. Математическая постановка проблемы.

Итак, наша задача сводится к численному решению уравнения (3)по известным начальным условиям, то есть по известному значениюx(0) иx’(t=0). Это – не что иное, как задача Коши для соответствующего дифференциального уравнения второго порядка. Проблема заключается в выборе способа численного интегрирования нашего уравнения.

В данной задаче применяются два метода численного интегрирования, один из которых является одношаговым, а другой многошаговым. Базовый метод интегрирования в данной реализации – метод Рунге-Кутта 4-го порядка точности. Помимо этого в задаче используется метод Адамса (или Адамса-Башфорта). Особой необходимости в использовании данного метода для анализа поведения системы в обычных условиях не было, но таковая возникла при рассмотрении процессов, происходящих в системе при процессах быстрого установления стационарного состояния при начальных условиях, достаточно близких к предельным циклам для данных значений параметров, когда метод Рунге-Кутта не приводил к приемлемому результату.

МЕТОД РУНГЕ-КУТТА.

Краткий алгоритм:

Метод Рунге-Кутта обладает значительной точностью и, несмотря на сою трудоёмкость, широко используется при численном решении дифференциальных уравнений.

МЕТОД АДАМСА.

Этот метод численного интегрирования был разработан Адамсом в 1855 году по просьбе известного английского канонира Башфорта, изучавшего внешнюю баллистику.

Основная экстраполяционная формула Адамсаимеет вид:

Для начала интегрирования необходимо знать четыре начальных значения, определяющиеся из начального условия посредством какого-нибудь численного метода, например метода Рунге-Кутта.

2. Реализация программы.

Моделирование данной задачи происходит в рабочей среде математического пакета “Mathematica V 3.0”. Моделирование задачи состоит из трёх этапов. На первом происходит решение дифференциального уравнения двумя методами. Кроме того, методом Рунге-Кутта осуществляется численное интегрирование уравнения свободных колебаний, которое используется для сравнительного анализа колебательных процессов. В качестве параметров задаются значения коэффициента затухания, величина малого параметра а и частота колебаний.

Во второй части программы идет построение основных графиков, необходимых для анализа задачи, а именно зависимостей обобщённой скорости и координаты от времени и фазовая плоскость. Последняя строится как методом Рунге-Кутта, так и методом Адамса. Наконец, в третьей части происходит сравнение исследуемого колебательного процесса с процессом затухающих колебаний.

2. АНАЛИЗ УРАВНЕНИЯ ВАН-ДЕР-ПОЛЯ И ЕГО РЕШЕНИЯ.

Прежде всего, необходимо ответить, что уравнение Ван-дер-Поля обладает той особенностью, что оно не имеет точного аналитического решения. Поэтому возможно два принципиально различных пути исследования этого уравнения. Во-первых, оно может быть исследовано, а, точнее, решено численно (например, так как указано в предыдущей части работы). А во-вторых, можно попробовать свести данное уравнение к некоему, более простому и удобному для исследования математическими методами. Подобный способ исследования уравнения Ван-дер-Поля был применён в первой части работы. В этой части работы этот способ будет дополнен первым методом на основе построенной выше программы. При этом основной упор будет сделан на качественное описание происходящих в системе физических процессов.

Основой для получения уравнения Ван-дер-Поля служило уравнение затухающих колебаний в физической (в частности, механической или электрической) системе. Основой для него, в свою очередь, служит уравнениегармонических колебаний:(17)

Гармоническому движению системы соответствует замкнутая фазовая траектория на фазовой плоскости (эллипс). Вообще, в общем случае сложного периодического движения фазовая траектория может иметь сложную форму, но всегда является замкнутой.

Если колебания в системе идут с потерей энергии (что всегда бывает в реальных физических системах), то мы приходим к процессу затухающих колебаний, описываемых уравнением (4). Вид фазовой плоскости для затухающих процессов показан на рисунке 1. Фазовый портрет представляет собой скручивающуюся к началу координат спираль. Из любого начального положения ( при малых значениях коэффициента или декремента затухания) изображающая точка с течением времени приближается к началу координат, являющемуся точкой устойчивого равновесия – устойчивым фокусом.

Затем были рассмотрены колебания с отрицательным «затуханием», изображённые на рисунке 2. Фазовый портрет отличается от портрета на рис.1. только тем, что спираль раскручивается и изображающая точка удаляется от начала координат. Точка x=0,y=0 является особой точкой типа неустойчивого фокуса.

В нашем случае, мы имеем нелинейность во втором слагаемом, которая качественно меняет схему происходящих в системе процессов. Из самого вида уравнения видно, что система вполне может стремиться к некоему стационарному состоянию, в некоем роде, аналогичному тому, что мы видели при рассмотрении гармонических колебаний. В случае автоколебательной системы, обладающей устойчивым стационарным состоянием (что, конечно же, зависит от ограничений на значения а и  ), на фазовой плоскости имеется замкнутая кривая , к которой приближаются соседние фазовые кривые. Соответствующая начальному (линейному в первом приближении) этапу фазовая траектория имеет вид раскручивающейся логарифмической спирали (особая точка типа неустойчивого фокуса).

Когда с ростом амплитуды колебаний начинает проявляться нелинейность системы, увеличение радиуса спирали замедляется и в пределе (при t) фазовая траектория превращается в окружность радиуса А’ , равного стационарной амплитуде автоколебания. Значение А’ можно получить методом медленно меняющихся амплитуд. Точное его значение достаточно громоздко; оно получается из рассмотрения зависимости амплитуды А колебаний от времени, которое само имеет достаточно сложный вид. Однако в первом приближении (линейным относительно разложение в ряд Фурье), мы получим, что квадрат радиуса предельного цикла A’ будет обратно пропорционален величине а. Рис3.(а,б).

Если начальное положение изображающей точки задать вне окружности радиуса предельного цикла, то движение изображающей точки будет происходить по скручивающейся спирали до перехода на окружность радиуса предельного цикла. В силу устойчивости стационарного состояния автогенераторов с мягким самовозбуждением, при любых начальных условиях изображающая точка переходит на окружность радиуса предельного цикла. Предельный цикл и есть та изолированная замкнутая кривая на фазовой плоскости, к которой стремятся соседние фазовые траектории.

По мере движения изображающей точки по спирали отклонение от предельного цикла убывают по экспоненте в зависимости от величины коэффициента затухания  . Рассмотренная выше устойчивость предельного цикла носит название орбитной или орбитальной устойчивости.

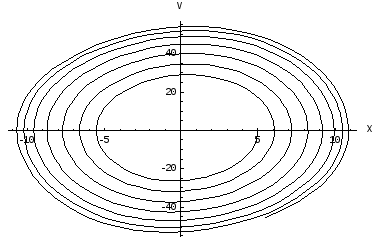
Рис 3. (а)

Ф а=0.03

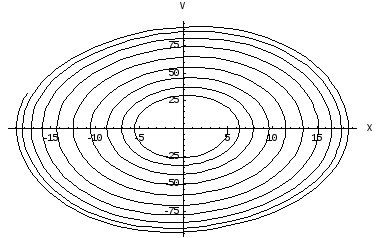
(б)

а=0.01

Таким образом, получаем, что время установление колебаний зависит только от коэффициента затухания по экспоненциальному закону. От частоты w зависит густота и, в конечном счёте, форма колебаний. Амплитуда же и характер стремления к предельному циклу зависят от начальных условий (X’(t=0) и X(0)), а также от величины модулирующего параметра а. Характер изменений отражен на графиках ниже.

Рис 4.

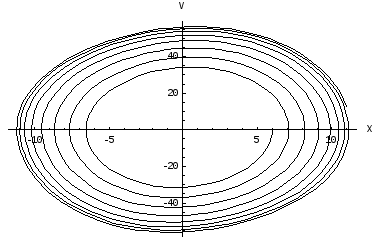
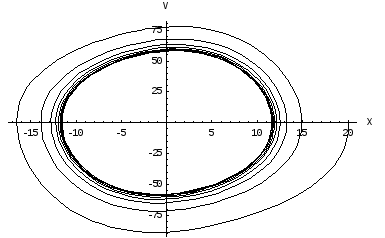Внешний режим

X(0)=20

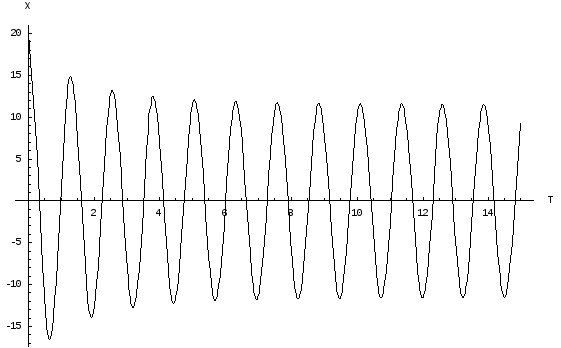
Колебания устанавливаются извне. (А’<X(0)). При этом коэффициент а – постоянен.

Рис 5.

Внутр. режим

X(0)=6

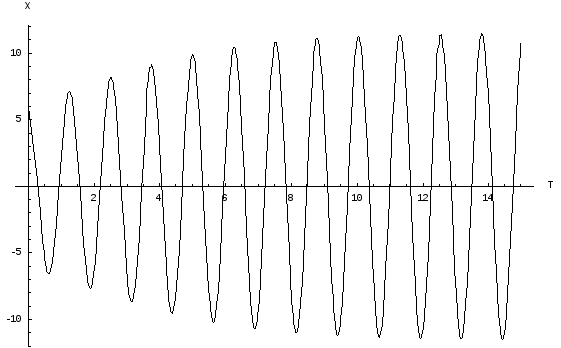
Колебания устанавливаются изнутри. (А’>X(0)). При этом коэффициент а – постоянен.

Таким образом, мы изучили все основные особенности процессов, происходящих в системе Ван-дер-Поля; рассмотрели их и с теоретической, и с практической точки зрения. Провели не только аналитическое, но и численное исследование задачи, получив результаты в наглядном виде. В работе была сделана попытка сравнительного анализа данного уравнения с хорошо известными линейными процессами. Все результаты проверены компьютерным модулированием.