Линейная алг. Заочное

Расширенная матрица системы

≠	11	12	1
	21	22	2	1
=					− расширенная матрица системы
				2
	1	2

– это матрица системы дополненная столбцом свободных членов.

Ранг матрицы равен максимальному числу ее линейно независимых строк.

Поэтому, если строки - линейно независимы, то	= ,
если линейно зависимы, то ( ) < .

Теорема. Кронекера-Капелли

Система линейных уравнений совместна тогда и только тогда, когда

ранг матрицы системы равен рангу расширенной матрицы этой системы.

(без док-ва)

Для совместных систем линейных уравнений верны следующие теоремы:

1.Если = , то система имеет единственное решение.

2.Если < , то система неопределенная (имеет бесконечное множество решений).

Пусть = < ,

Тогда переменных 1, 2, , называются базисными, если определитель матрицы из коэффициентов при них (т.е. базисный минор) неравен 0.

Остальные − переменных называются свободными.

Базисное решение – решение, в котором все свободные переменные равны 0.

Каждому разбиению переменных на базисные и свободные

соответствует одно базисное решение, а число способов разбиений
меньше или равно Сnr		, где Сnr		- число сочетаний из n элементов по r
элементов. С r =		!
	! − !
n

Метод Гаусса

Достоинства:

1.Менее трудоемок.

2.Позволяет однозначно установить, совместна система или нет, а в случае совместности найти ее решения (единственное или бесконечное множество).

3.Дает возможность найти максимальное число линейно независимых уравнений – ранг матрицы системы.

Метод Гаусса – метод последовательного исключения переменных

–заключается в том, что

спомощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида (прямой ход метода Гаусса),

из которой последовательно, начиная с последних по номеру переменных, находят все остальные переменные (обратны ход метода Гаусса).

Пример. Решить систему уравнений методом Гаусса.

1 + 2 − 3 = 2 −21 + 2 + 63 = 2

1 + 22 + 3 = 6

Решение.

1 + 2 − 3 = 2			∙ 2 ∙ −1
−21 + 2 + 63 = 2
1 + 22 + 3 = 6
1 + 2 − 3 = 2			∙ − 1
32+43 = 6
2 + 23 = 4							3
1 + 2 − 3 = 2
32+43 = 6			прямой ход завершен.
2	3	= 2
		3

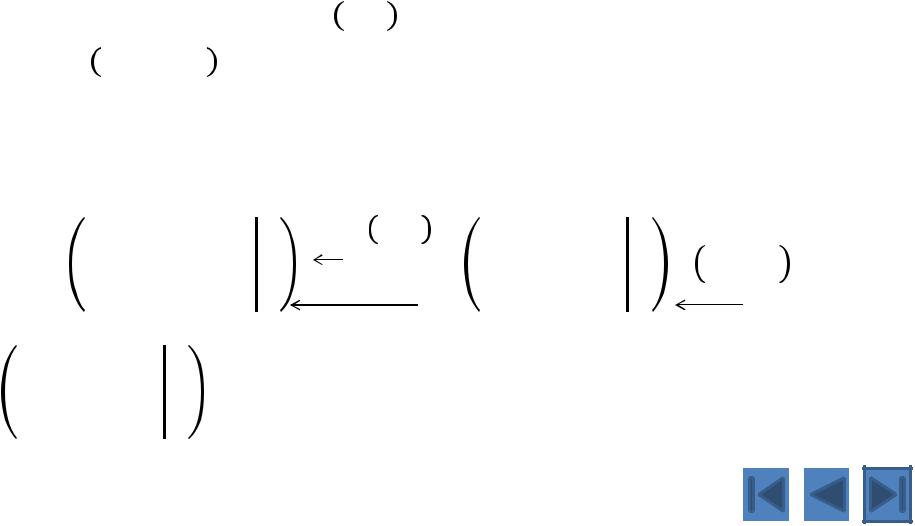
Обратный ход метода Гаусса:
	2	3	= 2		= 3
			3	3
3 2 + 4 3 = 6	3 2+4 ∙ 3 = 6			2 = −2
1 + 2 − 3 = 2	1 + −2 − 3 = 2				1 = 7
Ответ: 7; −2; 3

Для сокращения записей обычно не пишут неизвестные, а выполняют преобразования расширенной матрицы системы.

	1 1		−1 2		∙ 2		∙ −1			1	1	−1 2			−1
	−2 1		6	2						~ 0	3	4	6	∙			3	~
	1	2	1	6						0	1	2	4
1	1	−1 2
~ 0	3	4 6 Запись обратного хода прежняя.
0	0	2 3 2

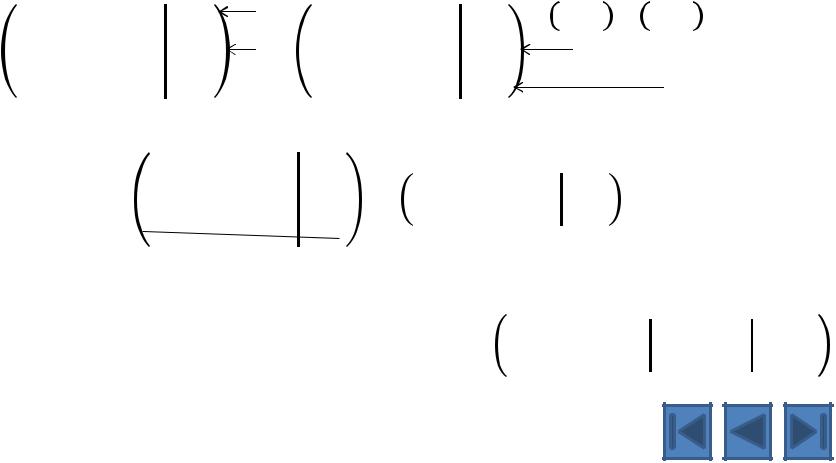
Пример. Решить систему уравнений методом Гаусса.

	2 1 − 2 + 3 − 4 = 5
	1 + 2 2 − 2 3 + 3 4 = −6
	3 1 + 2			− 3 + 2 4 = −1
Решение.
2−1 1 −1	5		~	1 2 −2 3	−6 ∙ −2 ∙ −3					~
1 2 −2 3	−6			2−1 1 −1	5
3 1 −1 2	−1			3 1 −1 2	−1

~ 1 2 −2 3 −6 ~ 1 2 −2 3 −6 0−5 5 −7 17 0−5 5 −7 17 0−5 5 −7 17

rang A = 2

Переменные	, принимаем за базисные базисный		1	2 ≠ 0
1	2	минор	0	−5

3, 4 - свободные переменные.

Обратный ход метода Гаусса.

Запишем систему уравнений, соответствующих полученной матрице

							1 + 2 2 − 2 3 + 3 4 = −6
							− 5 2 + 5 3 − 7 4 = 17
Выразим базисные переменные через свободные
						1 + 2 2 = 2 3 − 3 4 − 6
						− 5 2 = −5 3 + 7 4 + 17
										7			17
							2 = 3 −				4		−
										5				5
							7			17
			1 = −2 3 −						4 −				+ 2 3 − 3 4 − 6
								5		5
	= − 1			+ 4
1	5		4		5		Общее решение системы. (базисные
= −		7			−	17
2	3	5	4			5

переменные выражены через свободные)

Общему решению соответствует бесконечное множество частных решений.

Пусть 3 = , 4 = , a, b – любые числа,

тогда = − 1		+ 4	;		= − 7	− 17.
1	5	5		2	5	5

Произвольное частное решение:

− 15 + 45 ; − 75 − 175 ; ; .

Базисное решение:

3 = 0, 4 = 0 45 ; − 175 ; 0; 0

Замечание. В процессе последовательного исключения

неизвестных могут появиться уравнения вида

0 1 + 0 2 + + 0 = С

Если С ≠ 0, система несовместна.

Если С = 0, то такое уравнение отбрасывается.

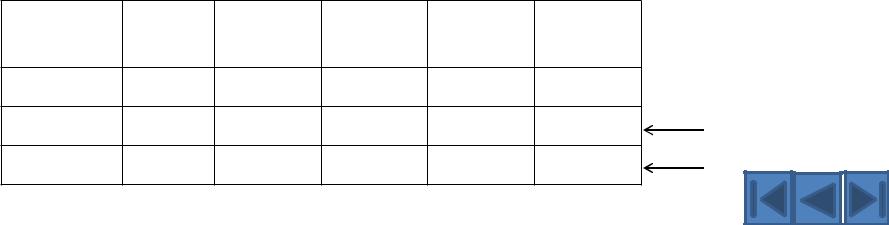
Метод Жордана-Гаусса

Метод полного исключения неизвестного, т.е. переменные принятые за базисные остаются только в одном уравнении (каждая в своем) из остальных уравнений они исключаются.

В итоге обратный ход не требуется. Рассмотрим на примере.

Преобразовываем расширенную матрицу системы, не записывая соответствующие уравнения.

Матрицы будем оформлять в виде таблиц Гаусса.

1 + 2 + 3 + 4 = 3

1 + 22 + 24 = 51 + 32 − 3 + 34 = 7

Базисные

перемен

x1

1	2	3	4

	1	1	1	3	1
1
1	2	0	2	5
1	3	-1	3	7

	Базисные
				1		2		3		4
	перемен
	x			1		1		1		1		3
	1															1
	x2			0		1		-1		1		2
				0		2		-2		2		4
	Базисные
				1		2		3		4
	перемен
	x			1		0		2		0		1
	1
	x	2		0		1		-1		1		2

Общее решение (базисные переменные выражаются через

свободные)

1 = 1 − 23

2 = 2 + 3 − 4

Базисное решение 3 = 0, 4 = 0 1; 2; 0; 0

C	r	C	2		4!	6
	n		4		2!2!

Количество различных базисных решений ≤ 6 Возможные пары базисных переменных:

1, 2	1, 3	1, 4
2, 3	2, 4	3, 4