2. Обоснование теоретических оценок временной сложности алгоритмов.

Временная сложность алгоритма построения выпуклой оболочки складывается из сложностей реализации каждого шага алгоритма. Таким образом, необходимо оценить сложность отдельных этапов:

1. Поиск лексикографического минимума с=lexmin{a₁,…,a_n} осуществляется в 2 этапа.

На 1 этапе однократным просмотром массива ищутся точки с минимальной первой координатой. Сложность такой операции составляет О(n), где n – число элементов массива.

На 2 этапе поиск точки с минимальной второй координатой среди подмножества точек с минимальной первой координатой также выполняется посредством однократного просмотра массива. В худшем случае количество точек с минимальной первой координатой совпадает с размерностью исходного массива (случай, когда все точки имеют одинаковую первую координату). Поэтому сложность такой операции поиска не превышает О(n).

2. Перенос системы координат в точку с=lexmin{a₁,…,a_n} осуществляется проходом по всему массиву с вычитанием соответствующих пар координат. Таким образом, сложность выполнения данного этапа порядка О(n).

3. Сортировка осуществляется с помощью 52-куч и сортируется алгоритмом сортировки 50-слиянием.

Сложность сортировки с помощьюd-куч:

Рассмотрим оценку для сортировки с помощью d-куч.

Для этого нужно оценить сложность следующих этапов:

• Окучивание

• В цикле по количеству элементов в массиве операция удаления минимального (DeleteMin) из d-кучи.

Сложность операции окучивания:

Теорема.

Вычислительная сложность операции окучивания равна О(n).

Доказательство:

Операция окучивания заключается в последовательном погружении элементов, начиная с последнего элемента дерева.

Сложность погружения с высоты i составляет O(d(h-i)). Псевдокод операции погружения (Diving) описан в предыдущем разделе. Сложность этой операции определяется:

• сложностью операции поиска потомка с минимальным ключом (MinChild). Так как у каждого не листового узла, за исключением одного, ровно d потомков, то сложность операции MinChild порядка О(d).

• числом итераций цикла, в котором эта операция выполняется. В самом худшем случае, число итераций будет равно h.

Следовательно, для узла с произвольного уровня оценка погружения будет равна O(dh), а для узла с высоты i - O(d(h-i)).

В любом завершенном d-арном дереве с n узлами и высотой h имеется не более чем .

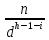Совокупная сложность окучивания дерева высоты h:

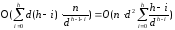Пусть h-i=j, то получим:

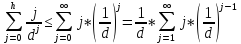
Так как при 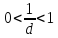это ряд сходится равномерно, то получим:

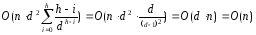ч.т.д.

Сложность операции удаления минимального (DeleteMin):

Фактически, данная операция включает в себя 2 операции:

• swap

• diving

Операция Swap выполняется за время О(1). И как было показано выше, операция погружения (diving) одного элемента выполняется за время О(dh). Оценим высоту дерева.

Теорема.

Высота h завершенного 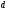-арного дерева удовлетворяет следующему неравенству.

Доказательство:

Минимальное число узлов в дереве высоты 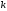определяется следующим соотношением

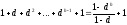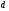, т.к. в завершенном -арном дереве каждый узел, за исключением, быть может, одного узла, содержит ровно-потомков. Тогда минимальное количество узлов будет, когда этот один узел имеет одного потомка.

Максимальное количество узлов в дереве высоты 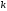определяется следующим соотношением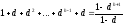. Тогда максимальное количество узлов будет, когда все узлы имеют ровно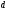-потомков.

Таким образом, число узлов в дереве высоты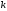удовлетворяет неравенству:

.

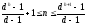Логарифмируем левую и правую части данного неравенства:

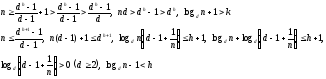
Отсюда получаем, 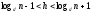, ч.т.д.

Таким образом, верхняя оценка сложности операции погружения всех n элементов (трудоемкость второго этапа сортировки) составляет

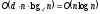
Итак, сложность сортировки с помощью d-куч равна 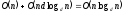=O(n*logn)