ATT00025-Экспертные оценки от Анохина

ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК

Таблица 21 Матрица коэффициентов парной ранговой корреляции

Эксперты	1	2	3	4	5	6	7	8	9
1	1	0,8	-0,7	0,8	0	-0,5	0,5	1	0
2	0,8	1	-1	1	0,4	-0,8	0,9	0,8	0,4
3	-0,7	-1	1	-1	-0,5	0,7	-0,8	-0,7	-0,5
4	0,8	1	-1	1	0,4	-0,8	0,9	0,8	0,4
5	0	0,4	-0,5	0,4	1	-0,9	0,7	0	1
6	-0,5	-0,8	0,7	-0,8	-0,9	1	-1	-0,5	-0,9
7	0,5	0,9	-0,8	0,9	0,7	-1	1	0,5	0,7
8	1	0,8	-0,7	0,8	0	-0,5	0,5	1	0
9	0	0,4	-0,5	0,4	1	-0,9	0,7	0	1

рица коэффициентов парной ранговой корреляции 9-ти экспертов, оценивавших соотношение различных типов поведения оператора в экспертизе «Оператор».

Зададимся пороговым значением ρ пор=0,7 и сформируем матрицу «сильных» связей (табл. 22). Из этой матрицы видно, что наибольшим количеством «сильных» связей (5 единиц) обладают эксперты 2, 4, 7.

Таблица 22

Матрица «сильных» связей

Эксперты	1	2	3	4	5	6	7	8	9
1	1	1		1				1
2	1	1		1			1	1
3			1			1
4	1	1		1			1	1
5					1		1		1
6			1			1
7		1		1	1		1		1
8	1	1		1				1
9					1		1		1

121

ГЛАВА 5

Выберем первого из них (эксперт 2) в качестве лидера первой группы. Сформируем шаблон: V={110100110}. Очевидно, что к формируемой группе добавляются эксперты 1, 4, 7, 8. После добавления эксперта 7 шаблон корректируется: V={110110111}, в результате чего к группе присоединяются еще и эксперты 5, 9. Предварительный список группы – 1, 2, 4, 5, 7, 8, 9, а ее численность – 7 экспертов. Откорректируем список, удаляя из него экспертов, имеющих менее четырех «сильных» связей. Этим свойством обладают эксперты 5 и 9. Окончательный состав первой высокосогласованной группы – 1, 2, 4, 7, 8.

Легко увидеть, что вторую группу составляют эксперты 3, 6, третью – эксперты 5, 9.

Из рассмотренного алгоритма видно, что на процесс формирования группы оказывают влияние два параметра: пороговое значение КПРК, определяющее понятие «высокосогласованные оценки», и 50% -ный барьер включения эксперта в группу.

Значение второго параметра обусловлено принципом большинства, применение которого в данном случае уместно. Исследуем подробнее процедуру выбора порогового значения.

Наиболее влиятельным фактором в процессе выделения групп является общая картина согласованности мнений. Если оценки всех экспертов хорошо согласованы, то количество «сильных» связей у каждого из них будет близко к общему числу экспертов, и тогда практически все они составят одну высокосогласованную группу. Если же общая согласованность мнений низка, то каждый эксперт может стать лидером своей собственной высокосогласованной группы, состоящей из него одного.

Очевидно, что подобные экстремальные ситуации крайне редки и проблема выбора порогового значения в них не стоит. Остановимся на задаче выбора ρ пор в среднем случае, когда при удовлетворительной общей согласованности возможно образование нескольких высокосогласованных групп, причем чаще всего среди них выделяется одна, заметно превосходящая по численности все остальные. Назовем та-

кую группу доминирующей.

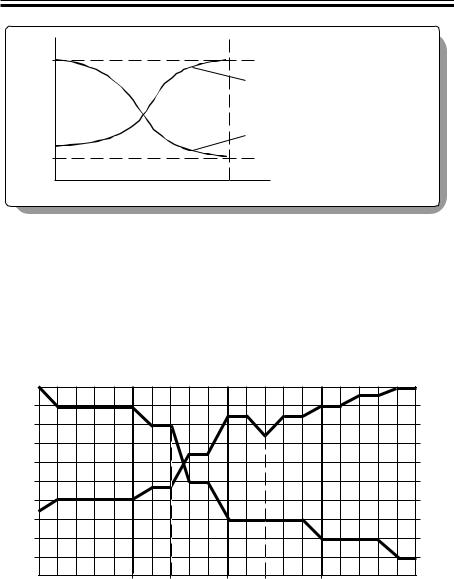
На рис. 28 показан вид зависимости численности доминирующей группы и коэффициента ее конкордации от порогового значения ρ пор. Из графика видно, что при слишком низком значении ρ пор эта группа хотя и будет достаточно многочисленной, однако в нее войдут экспер-

122

ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК

W=1			Рис. 28. Формы зави-
		W	симостей W(ρ ïîð) è
			M (ρ ïîð ):
			M – количество экс-
		M	пертов в домини-
			рующей группе;
M=1			W – коэффициент
			конкордации
0	1	ρ ïîð

ты с довольно высоким разбросом мнений. Такая группа характеризуется слабой конкордацией, а следовательно – низкой статистической значимостью обобщенного мнения.

Слишком высокое пороговое значение, как правило, приводит к большому дроблению экспертов на малочисленные, однако очень высокосогласованные группы. Конкордация таких групп весьма сильна, хотя статистическая значимость результата может также оказаться невысокой из-за малого количества экспертов в группе.

M							W
10							1,0
9							0,9
8							0,8
7							0,7
6							0,6
5							0,5
4							0,4
3							0,3
2							0,2
1							0,1
0							0
	0	0,25	0,35	0,5	0,6	0,75	ρ ïîð
Рис. 29. Пример анализа порогового значения: ρ ïîð=0,35–0,4 – ðåêî-
мендуемые значения, ρ ïîð=0,6 – смена						доминирующей группы
							123

ГЛАВА 5

Очевидно, что достигаемый уровень конкордации является основным критерием выбора порогового значения. Требования к этому уровню обычно определяются исходя из семантических аспектов экспертизы, однако можно с уверенностью утверждать, что он не должен быть меньше 0,4– 0,5.

Отметим также, что на обеих кривых выделяется участок их интенсивного изменения. Этот участок характеризуется сильным ростом согласованности, сопровождаемым уменьшением численности доминирующей группы. Можно предположить, что оптимальное пороговое значение расположено именно на этом участке. Так, опыт обработки многочисленных экспертиз показал, что это значение обычно находится непосредственно перед или после точки пересечения кривых, в окрестности которой наблюдается скачкообразное падение М

(рис. 29).

Кроме того, рис. 29 иллюстрирует еще одну ситуацию, когда с увеличением ρ пор происходит перегруппировка экспертов и доминирующей становится совсем другая группа. Такая ситуация характеризуется локальными флуктуациями значений M и W.

5.4. Синтез обобщенного мнения

Настоящий этап является последним в цепочке процедур обработки экспертных оценок. Его цель – объединить несколько различных оценок одного и того же объекта экспертизы в одну, получив при этом «обобщенное мнение». Известны два принципа такого объединения: статистический и алгебраический.

Статистические методы основаны на предположении, что существует некоторая «истинная» оценка, и отклонения оценок экспертов от этой истинной оценки происходят в силу случайных причин. Задача статистических методов состоит в том, чтобы восстановить это истинное значение с наименьшей погрешностью. Суть алгебраических методов заключается в определении в качестве результирующей той оценки, которая наименее всего отстоит от остальных экспертных оценок. Типичным воплощением статистического подхода является среднее арифметическое, алгебраического подхода – медиана Кемени.

Для каждого из рассмотренных в разд. 5.1 видов результата экспертного оценивания существуют свои подходы к обобщению. Их ус-

124

ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК

ловные названия с		Таблица 23
указанием типа оце-	Классификация методов синтеза
нок, для обработки	обобщенного мнения
которых они предна-
			Òèï
значены, приведены
	Метод		обобщаемых
в табл. 23.			оценок
В предыдущем
	1. Среднее арифметическое
разделе было пока-			X, Λ
	2. Взвешенное среднее
зано, что в ряде слу-
	3. Медиана распределения
чаев среди экспер-
тов образуются не-	4. Сумма рангов		R
сколько групп, про-	5. Принцип Кондорсе
тиворечащих друг
	6. Медиана Кемени		R, Π
другу. Обобщать та-
кие оценки, безусло-	7. Мажоритарная выборка		C
вно, нельзя. Единст-
венный выход в по-
добных обстоятельствах – синтез нескольких обобщенных мнений, от-
ражающих позицию каждой из групп, и предоставление аналитику
права самому определять, какое из них верно.
В дальнейшем изложении мы, по-прежнему, будем предполагать,
что обобщаются оценки m экспертов, однако под m		может пониматься

как общее число экспертов-участников опроса, так и число экспертов, составляющих одну из высокосогласованных групп. Рассмотрим более подробно методы обобщения результатов различного типа.

Обобщение ранжирований. Для обобщения ранжирований используются три метода: суммирование рангов объектов, медиана Кемени и принцип Кондорсе. Принцип Кондорсе предназначен для обобщения лишь строгих (простых) ранжирований, в то время как для первых двух методов тип ранжирования не играет никакой роли.

Наиболее простым по реализации и вместе с тем наименее сильным с точки зрения «истинности» результата является суммирование рангов. Этот подход предполагает получение обобщенного вектора рангов в результате ранжирования сумм рангов объектов экспертизы.

Как уже было показано в табл. 10, для каждого объекта экспертизы ai подсчитывается сумма рангов S(ri ), выставленных этому объекту всеми (или только высокосогласованной частью) экспертами:

125

ГЛАВА 5
S (ri ) = ∑m rij ,	(19)
j =1
где rij – ранг i-го объекта по мнению j-го эксперта.
После этого объекты упорядочиваются по возрастанию сумм и
ранжируются: первый по порядку объект с минимальной суммой
объявляется наиболее предпочтительным и ему присваивается мини-
мальный, а последнему – максимальный ранг; для объектов с одинако-
выми суммами рассчитывается связный ранг. Полученное ранжиро-
вание считается обобщенным мнением R*.
Принцип Кондорсе относится к наиболее ранним исследованиям
(конец XVIII в.) и принадлежит французским ученым Кондорсе и Бор-
да. Кондорсе впервые обратил внимание на недостаточность проце-
дуры определения наиболее приоритетного объекта по правилу боль-
шинства.
Согласно предложенному им принципу, для каждой пары объек-
тов (ai , aj ) подсчитывается si j – число экспертов, считающих, что
объект ai более предпочтителен, чем aj . Объект ai объявляется наи-
лучшим (наиболее приоритетным или объектом Кондорсе), если для
всех i ≠ j соблюдается неравенство sij ≥	sj i . Этому объекту присваива-
ется ранг 1 и он исключается из дальнейшей обработки, а процедура
поиска объекта Кондорсе повторяется уже для оставшихся объектов.
При использовании принципа выбора Кондорсе может возникнуть
парадокс, когда объекта Кондорсе не существует из-за нетранзитив-
ности коллективных ранжирований. Вероятность возникновения та-
кого парадокса – около 9%, а в экспертизах, где мнения экспертов су-
щественно различаются – выше.
Далее в табл. 24, 25 приведен пример определения объекта Кон-
дорсе по ранжированиям четырех объектов пятью экспертами. Отме-
тим, что принцип Кондорсе позволил определить наилучший объект
среди двух с одинаковой суммой рангов, что невозможно сделать, при-
меняя метод суммирования рангов. Обобщенное ранжирование по
принципу Кондорсе в этом примере совпадает с вектором рангов вто-
рого эксперта R* = R .

2

Медиана Кемени. Основу данного метода составляет предположение о том, что результирующий (обобщенный) вектор рангов R*

126

ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК

										Матрица рангов					Таблица 24
			Объекты					Ранжирования экспертов							Суммы
															рангов
					ai
								R1		R2	R3	R4		R5	S(r	)
															i
					1		3			4	4	4		4	19
					2		2			3	2	3		1	11
					3		1			2	3	1		3	10
					4		4			1	1	2		2	10
					Таблица 25
Матрица относительных
	предпочтений
											s43=3: 3 эксперта
Объекты		1		2		3		4
													(å2, å3, å5) считают,
1		-		0		0		1
													что объект a4 более
2		5		-		2		2
													предпочтителен
3		5		3		-		2					(имеет меньший
													ðàíã), ÷åì a3
4		4		3		3		-

Объект Кондорсе

должен быть расположен как можно ближе к экспертным ранжирова-
ниям R1 ... Rm. Такое результирующее ранжирование называется ме-
дианой Кемени					) = min ∑m d
	R*(R ...R			m			(R, R	j	) ,
			1		R j =1
где d(R,Rj) – расстояние между ранжированием j-го эксперта и произ-
			вольным вектором рангов R.
Чтобы вычислить расстояние, для каждого ранжирования R по-
строим матрицу отношений
П(R			) ={π	( ) | i, j=1... n},
				ij
			1, если объект ai более предпочтителен, чем aj (ri< rj),
где π	ij	=	0, если объекты равноценны (ri= rj),
			–1, если объект a			i	менее предпочтителен, чем a			(r	>r ).
									j	i	j

127

ГЛАВА 5

Выбрав в качестве меры близости модуль разности соответству-
ющих элементов матриц отношений, можно определить расстояние
между ранжированиями двух экспертов следующим образом:
d (R , R		ν	) = 1 ∑n				π	(µ) − π			(ν)		.
µ			2 i, j		=1			ij			ij
Более подробное определение мер близости и комбинаторный ал-
горитм нахождения медианы Кемени приведены в монографии [9].
Проиллюстрируем поиск медианы Кемени на примере, используя
данные из табл. 24. Матрицы отношений
	0 −1			−1 1								0		−1	−1		−1					0 −1 −1		−1
Π (R )=			1 0	−1 1 , Π					(R )=			1 0			−1		−1 ,		Π (R )=			1 0 1		−1 ,
1			1 1 0 1						2			1 1 0					−1		3			1 −1 0		−1
		−1 −1		−1 0									1 1 1 0									1 1 1 0
			0 −1 −1		−1							0		−1	−1		−1
Π (R )=			1 0	−1	−1 , Π				(R )=				1 0 1 1 .
4			1 1 0 1						5			1		−1 0			−1
			1 1 −1 0									1		−1 1 0
																						Таблица 26
В табл.26 приведены											Расстояния между ранжированиями
расстояния между всеми													R1			R2			R3		R4		R5	Σd
ранжированиями. Из при-
										R1		0					6		8		4		6	24
веденных	сумм			расстоя-
										R2		6					0		2		2		4	14
ний видно, что ранжирова-
ние, выполненное вторым										R3		8					2		0		4		2	16
экспертом, наиболее близ-										R4		4					2		4		0		6	16
ко к медиане, однако не
										R	5	6					4		2		6		0	18
обязательно является ею.

d(R5,R2)

Обобщение относительных значимостей и численных оценок.

Как уже отмечалось, для обобщения таких оценок применяются методы, основанные на вычислении среднего (арифметического или взвешенного) либо на частотном анализе распределения.

Среднее арифметическое является наиболее распространенным способом из-за своей простоты и незатейливости. Элемент результирующего вектора вычисляется как арифметическое среднее соответ-

128

ОБРАБОТКА ЭКСПЕРТНЫХ ОЦЕНОК

ствующих оценок:

λ

* =

1

∑m

λ

,

(20)

где λ

i

m j

=1

ij

ij

–относительная значимость i-го объекта по мнению j-го эксперта.

Среднеарифметический вектор обладает двумя основными недо-

статками. Во-первых, он уравнивает всех экспертов, независимо от их

компетентности и других качеств. И во-вторых, он накапливает и

суммирует все ошибки и погрешности, содержащиеся в обобщаемых

оценках.

Среднее взвешенное, если и не полностью ограждает от этих непри-

ятностей, то, по крайней мере, предоставляет средство, позволяющее

управлять ими. Этим средством являются весовые коэффициенты,

присваиваемые всем экспертам в каждой конкретной экспертизе. Эле-

мент результирующего вектора вычисляется как взвешенное среднее

соответствующих оценок:

λ

* =

∑m v

j

λ

ij

,

(21)

i

j =1

где vj

– нормированный вес j-го эксперта ( ∑m v

j

=1).

j =1

По существу, среднее арифметическое тоже является взвешенным, но

при этом веса всех экспертов одинаковы и равны 1/m.

Определить вес эксперта можно, основываясь на данных о его

компетентности либо на анализе отклонений его оценок.

В первом случае весом эксперта может быть любая линейная ком-

бинация из коэффициентов компетентности, осведомленности, степе-

ни надежности, противоречивости и других количественных показа-

телей его качеств.

Во втором случае весовой коэффициент j-го эксперта обратно

пропорционален его вкладу в общую дисперсию оценок:

v

j

=

2

− s

j

/ ∑m s

j

,

m

j

=1

=∑n ∑

m (λ

где s

j

ij

− λ

ik

)2

– сумма квадратичных отклонений оценок j-

i

=

=

го эксперта от остальных оценок .

1 k

1

129

ГЛАВА 5

Более корректной, однако менее сильной является формула, ис-

пользующая отношения между суммами sj для расчета весовых коэф-

фициентов

m

s

min

v = s

/ (s

∑

) ,

min

i

j j =1

sj

где smin – минимальное значение sj

( j=1...m).

Диапазон значений весового коэффициента – v [0,1], а в случае

полного совпадения мнений (или одинаковой компетентности) экспер-

тов v=1/m.

Медиана распределения. Ранее в п. 5.2.3 уже рассматривался ана-

лиз оценок, основанный на вычислении выборочных квартилей x0,25,

x0,5 и x0,75, разбивающих упорядоченные оценки i-го объекта на четы-

ре равные по численности группы. Квартиль x0,5 называется медианой

распределения оценок и может рассматриваться в качестве результи-

рующего обобщенного показателя

x*=x

(i )

(22)

i

0,5

и x0,75 при этом характеризуют степень согласованно-

(квартили x

0,25

сти мнений).

Основная идея использования медианы в качестве обобщенной

оценки аналогична уже рассмотренной медиане Кемени – результиру-

ющие оценки должны быть расположены как можно ближе к эксперт-

ным. Приведенное выражение (22) является алгоритмом такого обоб-

щения для абсолютных численных оценок и баллов, являющихся неза-

висимыми случайными величинами. В случае же обобщения относи-

тельных значимостей необходим более сложный алгоритм поиска все-

го результирующего вектора целиком

Λ *= min ∑m d (Λ

, Λ

j

) ,

( ∑n λ

i

=1 ),

Λ

j =1

i =1

где d (Λ

, Λ

j) – расстояние между вектором относительной значимости

j-го эксперта и произвольным вектором Λ .

Очевидно, что мерой близости здесь является модуль разности от-

носительных значимостей, а расстояние вычисляется как

d (Λ µ, Λ ν ) = ∑n

λ iµ− λ iν

.

i =1

130