2.1.2 Загальна формула для визначення переміщень. Метод Мора

Розглянемо довільну плоску стрижневу систему (балку, раму, ферму тощо), навантажену заданими силами Р (рис. 2.7, а). Зусилля в до­вільному перерізі системи позначимо через М_р, Q_p, N_р. Нехай треба визна­чити переміщення (узагальнене) будь-якої точки системи в напрямі і – і.

Введемо допоміжний стан (рис. 2.7, б), що є заданою системою, навантаженою лише однією одиничною силою (узагальненою) , прикладеною в тій самій точціт і в напрямі шуканого переміщення Δ_іР. Зусилля в довільному перерізі допоміжного стану, спричинені дією одинич­ної сили , позначимо через,,.

У загальному випадку дії сил формула для переміщення містить шість доданків:

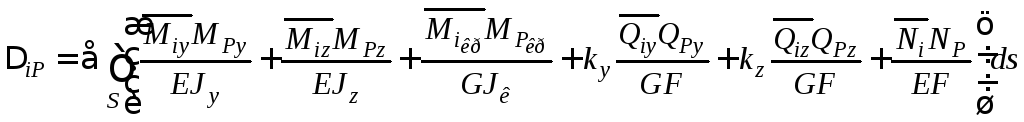. (2.8)

Індекси у, z у формулі (2.8) позначають головні осі, індекс «кр» – крутний момент. Зазначимо, що наведену формулу можна застосувати і для кривих стрижнів малої кривини.

Формулу (2.8) вперше було виведено Мором. Визначення переміщень за цією формулою часто називають методом Мора (dummy-load method, Maxweel-Mohr method, unit-load method). Зазна­чимо, що метод Мора – це найзагальніший метод визначення переміщень стрижневих систем. Його значення особливо велике при розрахунку ста­тично невизначуваних систем.

Здебільшого при визначенні переміщень у балках, рамах та арках мож­на знехтувати впливом поздовжніх деформацій і деформацій зсуву, вра­ховуючи лише переміщення, спричинені згинанням і крученням. Тоді фор­мула (2.8) для плоскої системи набирає вигляду

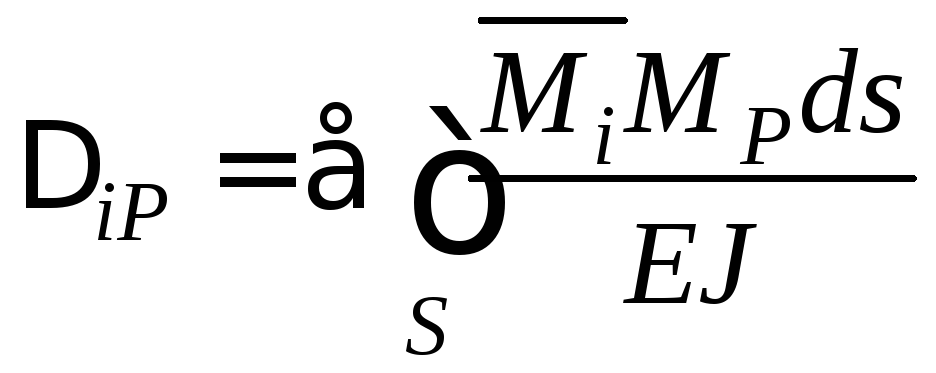. (2.9)

При просторовому навантажуванні, згідно з формулою (2.8),

. (2.10)

При визначенні переміщень вузлів шарнір­них ферм, що складаються з прямих стрижнів, у формулі Мора зберігається тільки один дода­нок:

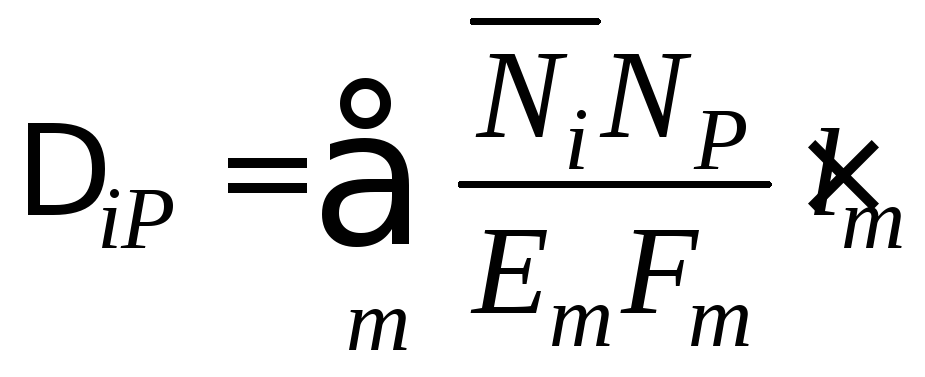. (2.11)

Ця формула має назву формули Максвелла.

Можна запропонувати таку послідовність визначення переміщень за методом Мора:

1. Будують допоміжну систему, яку наванта­жують одиничним навантаженням у точці, де треба визначити переміщення. Визначаючи лінійні переміщення, у заданому напрямі при­кладають одиничну силу, визначаючи кутові переміщення, – одиничний момент.

2. Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої (М_р, N_р, Q_p) і допоміжної (,,) систем.

2. Обчислюють інтеграли Мора (по ділян­ках у межах всієї системи). Як вже зазначало­ся, при розрахунку плоских балок, рам і арок виходять з формули (2.9), просторових систем – (2.10), ферм – (2.11).

4. Якщо обчислене переміщення додатне, то це означає, що його напрям збігається з вибра­ним напрямом одиничної сили. Від'ємний знак свідчить про те, що дійсний напрям шуканого переміщення протилежний напряму одиничної сили.

Розглянемо приклади застосування методу Мора для визначення переміщень у різних стрижневих системах.

Припустимо, що треба визначити прогин посередині прогону та кут повороту на опорі шарнірно обпертої балки (EJ = const), навантаженої рівномірно розподі­леним навантаженням інтенсивністю q (рис. 2.8, а), а також дослідити вплив поперечних сил на максимальний прогин.

1. Для визначення прогину посередині прогону прикладаємо в цьому місці допоміжної балки (рис. 2.8, б) одиничну зосереджену силу. В довільному перерізі першої ділянки балки (0 ≤ х ≤ l/2)

; .

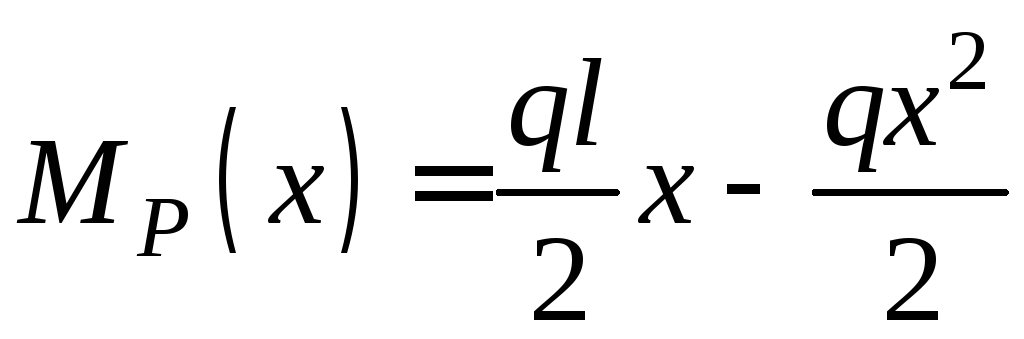Ураховуючи симетрію, дістанемо

.

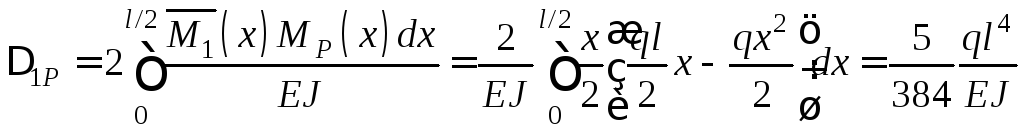Врахуємо вплив дотичних напружень на шуканий прогин, припускаю­чи, що балка має прямокутний переріз. Очевидно, при 0 ≤ х ≤ l/2

; .

На підставі формули (2.8) прогин, спричинений дією поперечних сил,

.

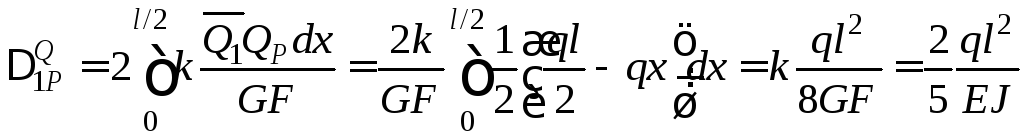При цьому враховано, що коефіцієнт форми для прямокутного перерізу

, а

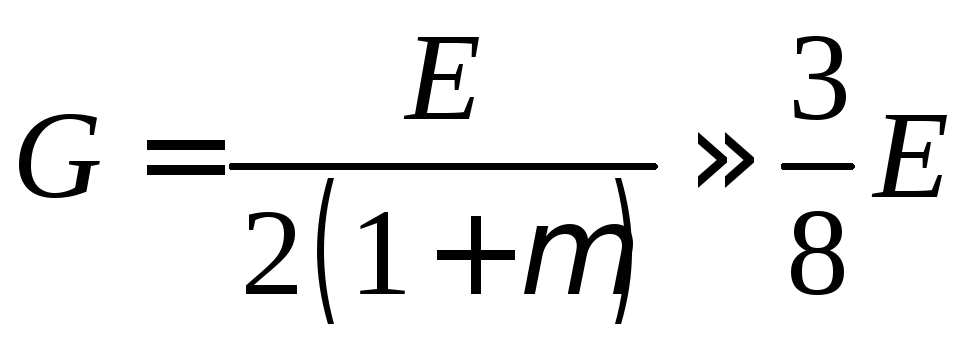
Підсумовуючи вирази для переміщень, знаходимо, що

.

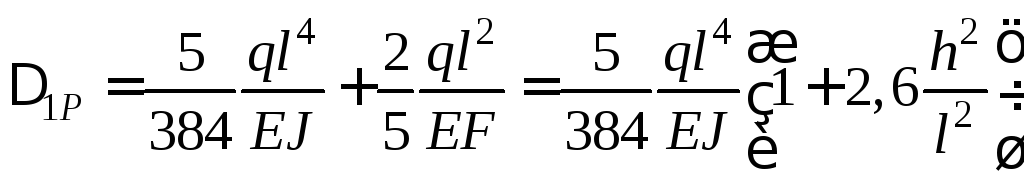Другий член у дужках, що відображує вплив поперечної сили, при відно­шенні висоти перерізу до довжини прогону h/l = 1/10 дорівнює 0,026. Отже, прогин, спричинений поперечною силою, становить менше ніж 3% прогину, спричиненого згинальними моментами.

2. Для визначення кута повороту опорного перерізу допоміжну балку навантажуємо одиничним моментом (рис. 2.8, в). При 0 ≤ х ≤ l/2 маємо

; ;

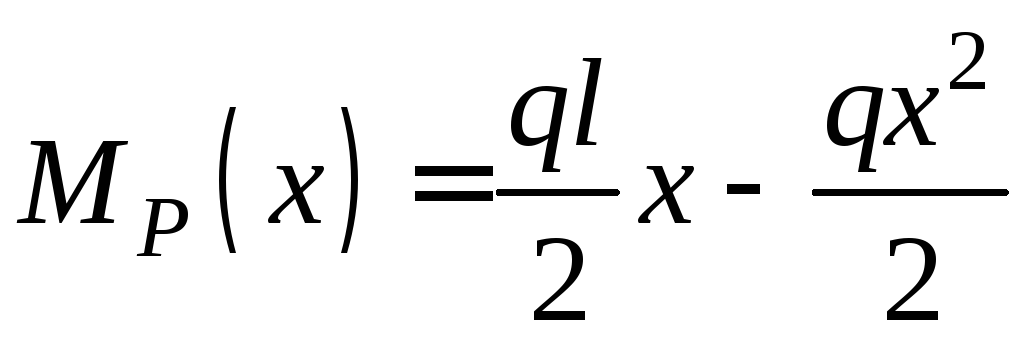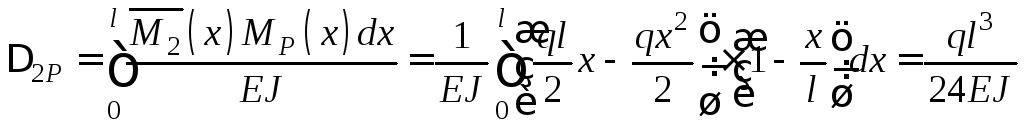. (2.12)

Додатний знак свідчить про те, що напрям повороту збігається з на­прямом одиничного моменту.

Визначимо вертикальне переміщення вузла В шарнірно-стрижневої сис­теми (рис. 2.9, а), яка складається з двох однакових стрижнів АВ і ВС пос­тійного поперечного перерізу. Допоміжну систему зображено на рис. 2.9, б.

Розглядаючи рівновагу вирізаного вузла В, знаходимо зусилля в стриж­нях для обох станів:

Стрижень N_P AB Р 1

ВС –P –1

З формули (2.11) маємо

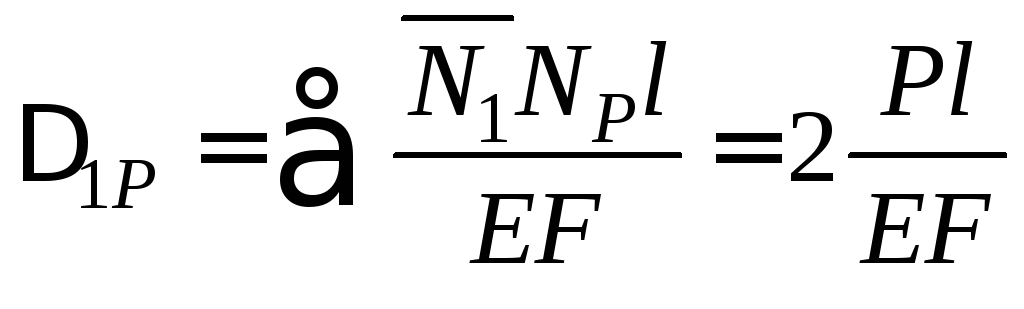(2.13)

Приклад. Розміщена в горизонтальній площині рама АВС (рис. 2.10, а) скла­дається з двох стрижнів однакового круглого поперечного перерізу. Визначимо верти­кальне переміщення точки С. Допоміжну систему зображено на рис. 2.10, б.

Переміщення Δ­­_1P можна визначити з формули (2.8). Для довільних перерізів двох ділянок маємо:

для І ділянки (0 ≤ х ≤ l/2)

;;;;

для ІІ ділянки (0 ≤ х ≤ l)

;;;;

(2.14)