теория автоматического управления

1.5./GOP=IQGBGR=IB;FEF=A?=F

Все сопротивления в Мом, С1 = 1 мкф, С2 = 0,5 мкф.

Для инерционного, интегрирующего и реального дифференцирующих звеньев:

R'2 = 1 МОм, R3 = 0,5 МОм, R'3 = 1 МОм.

										Таблица 1.1
	Значение сопротивлений для расчета параметров звеньев
Вари-		Инерционное			Реальное			Колебательное
		и интегрирующее			дифференци-
ант									звено
			звено		рующее звено
		R1	R'1	R2	R1	R"1	R1	R"1	R'2	R3		R'3
1		0,1	0,5	1	1	1	1	1	1	0,5		1
2		0,2	0,5	1	1	0,5	1	0,5	0,5	1		1
3		0,5	0,5	1	0,2	0,5	1	0,4	0,5	0,5		1
4		0,5	0,5	0,5	0,5	0,5	1	0,1	1	1		1
5		0,1	0,2	1	0,1	0,2	1	0,2	0,3	0,3		0,3
6		0,2	0,2	1	0,1	0,5	0,5	1	0,25	0,25		0,25
7		0,5	0,2	0,5	0,2	0,2	0,4	0,8	0,6	0,6		0,6
8		0,5	0,2	0,1	0,1	0,1	0,3	0,2	0,5	0,5		0,5
9		0,4	0,5	0,3	0,4	0,4	0,7	0,8	0,25	0,25		0,25
10		0,4	0,4	0,4	0,6	0,3	0,9	0,3	0,1	0,1		0,1
11		0,4	0,4	0,2	0,5	0,3	0,25	0,75	0,4	0,8		0,4
12		0,3	0,5	0,6	0,3	0,3	0,1	0,8	0,7	0,7		0,7
13		0,4	0,6	1	1	0,2	0,2	0,4	1	0,1		0,1
14		0,7	0,2	0,8	0,7	0,8	0,35	0,75	1	0,2		0,2
15		0,7	0,1	0,3	0,7	0,3	0,6	0,6	1	0,9		0,9
16		0,8	0,2	0,4	0,4	0,6	0,3	0,3	0,9	0,1		0,9
17		0,35	0,35	0,35	0,5	0,1	0,5	0,1	0,9	0,5		0,05
18		0,9	0,1	0,1	0,7	0,1	0,8	0,2	0,35	0,35		1

11

								Окончание табл. 1.1
Вари-	Инерционное			Реальное			Колебательное
	и интегрирующее			дифференци-
ант									звено
		звено		рующее звено
19	0,9	0,2	0,2	0,35	0,35	0,4	0,1		1	0,3	1
20	0,9	0,4	0,23	0,25	0,25	0,25	0,5		0,2	1	0,2
21	0,8	0,5	0,07	0,4	0,1	0,1	0,9		0,7	0,1	0,7
22	0,7	0,8	0,3	0,1	0,8	1	0,25		0,1	0,8	0,1
23	0,6	0,7	0,8	0,9	0,25	0,8	0,3		0,75	0,75	0,75
24	0,25	0,3	0,25	0,8	0,4	0,1	0,1		0,1	1	0,1
25	0,5	0,25	0,5	0,6	0,25	0,7	0,7		0,2	0,2	1

1.6."AOIBJMC@SQ;FM>KP=A@K.7(%@@OO>=<;FGA@=EF=A?=F

1.Запустить matlab.

2.После того как Matlab загрузится – появится приглашение.

3.>>

4.Ввести следующие команды:

5.cd work.

6.toat8.

7.Вам будет предложено ввести фамилию и номер группы. После этого будет задано 5 вопросов. Необходимо дать правильный ответ на любые 4 вопроса из 5, в противном случае следует вновь

выбрать toat8 и попытаться еще раз.

8.В случае правильных ответов откроется окно Microsoft Word с шаблоном курсовой работы. В ней нужно изменить значения коэффициентов К, Т, t на рассчитанные вами значения.

9.В Microsoft Word выбрать пункт меню Notebook-> Evaluate M-book. Matlab на основе введенных вами данных сделает необ-

ходимые расчеты и построит графики.

Возможные неисправности:

Не запускается Matlab. Решение: запустите Reinit Shares, который расположен на рабочем столе.

12

2.9"TT$/$1U"'081&$-/'(1$1"2,.$/$9'#)*1'2

".$/$:)91'2T-1+U""5($18$(

2.1.)QB=<=>=A@=<@HH=B=AC@G>?A;D;JBGFA=A@S

Динамический режим работы систем автоматического управления (САУ) наблюдается в том случае, когда система выведена из состояния равновесия. Ситуация, соответствующая динамическому режиму, является следствием изменения задающего воздействия или влиянием возмущающего воздействия (помех).

При изменении задающего или возмущающего воздействия в САУ

возникает переходный процесс. Основной задачей динамики САУ является описание поведения системы во время переходного процесса.

Решение задачи производится с помощью дифференциального уравнения системы, которое составляется в несколько этапов:

–разделение системы на отдельные звенья;

–составление дифференциального уравнения для каждого звена;

–используя законы преобразований уравнений при разных соединениях звеньев, составляют общее дифференциальное уравнение системы.

–В теории САР применяют следующие обозначения:

–Y,Y ',Y ", … Y (n) – регулируемая величина и ее производные;

–X, X ', X ", … X (n) – задающее воздействие и его производные;

–f , f ', f ", … f (n) – возмущающее воздействие и его производные. В общем виде для любой САР дифференциальное уравнение мож-

но записать следующим образом:

F1(Y, Y ', Y ", … Y (n)) = F2(X, X ', X ", … X (n); f, f ', f ", … f (m)) или если ис-

пользовать принцип суперпозиции функции:

F1(Y, Y ',Y ", … Y (n)) = F2(X, X ', X ", … X (n)) + F22(f, f ', f ", … f (m)).

Для решения дифференциального уравнения требуется знать входное воздействие, при выборе формы которого необходимо учесть:

–входное воздействие должно наиболее полно отражать динамические свойства системы – как система реагирует на входное воздействие – скоростную реакцию системы;

–решение дифференциального уравнения должно быть простым.

Этим условиям удовлетворяет единичная функция или единич-

51,	t 4 0
ный скачок: 1(t ) ! 6	t 7	.
80,		0

13

Для любой САР дифференциальное уравнение, выражающее зависимость регулируемой величины от задающего воздействия, записывается так:

а0 y (n) ' а1 y (n #1) '!' аn #1 y , ' аn y ! b0 x (m ) ' b1 x (m #1) '!' bm #1 x , ' bm x

В таком виде решение дифференциального уравнения представляется сложным, поэтому обычно переходят к алгебраической форме записи дифференциального уравнения. Для этого применяют опе-

раторный метод решения дифференциальных уравнений, используя прямое и обратное преобразование Лапласа:

dy(t )	! py( p);	d 2 y(t )	! p2 y( p);	9y(t )dt !	y( p)	.
		2
dt		dt			p

Дифференциальное уравнение может быть переписано в опера-

торной форме:

а0 pn y( p) ' а1 p(n #1) y( p) '!' аn #1 py( p) ' аn y( p) !

! b0 p(m ) x( p) ' b1 p(m #1) x( p) '!' bm #1 px( p) ' bm x( p), или

(а0 pn ' а1 p(n #1) '!' аn #1 p ' аn ) $ y( p) ! ! (b0 p(m ) ' b1 p(m #1) '!' bm #1 p ' bm ) $ x( p).

2.2..=B=V;<AGS@Q=B=<GI;PAGSHJAMC@@EF=AG

	y( p)		b p(m ) ' b p(m #1)			'!' b	p ' b
Введем: К ( p) !		!	0	1		m #1	m	.
			a pn ' a p(n #1)		'!' a
	x( p)						p ' a
			0	1		(n #1)	n

Представленное выше выражение называется передаточной функцией САР – это отношение изображения регулируемой величины к изо-

бражению задающего воздействия при нулевых начальных условиях.

Переходной функцией САР h(t) ●=●h(p) называется зависимость

регулируемой величины от времени, если в качестве задающего воз-

действия используется единичный скачок.

Комплексный коэффициент усиления (частотная передаточная

функция) K(jω) = K(p) – это отношение регулируемой величины к задающему воздействию, при условии, что задающее воздействие

представляет собой синусоидальное колебание:

14

x(t) = A0sinωt = A0e jωt, y(t) = A1sin(ωt + φ) = A1e(ωt + φ),

К ( j;) ! y( p) ! A1 e j : ! К (;)e j : . x( p) A0

Для инерционного звена первого порядка дифференциальное

уравнение имеет вид: T dy ' y ! Kx , тогда в операторной форме: dt

(Tp + 1) · y(p) = Kx(p),

а коэффициент передачи К ( p) ! К .

Tp '1

Переходная характеристика в операторной форме определяется из следующих соображений: y(p) = K(p) · x(p), y(t) = h(t), если

	x(t) =1(t).
		1		K ( p)	#1	<К ( p) =
	1(t ) !		; h( p) !		; h(t ) ! L	>		?	,
		p		p			p
						@		A

	где L-1 – обратное преобразование Лапласа.
		К		#	t
	h(t ) !			; h(t ) ! K (1 #e T ),
		p(Tp	'1)

где T – постоянная времени звена. Для интегрирующего звена:

t

К

К

К

y(t ) ! K 9x(t )dt ; y( p) !

x( p) ; К ( p) !

; h( p) !

; h(t) = Kt.

2

0

p

p

p

Для дифференциального звена:

T

dy

' y( p) ! K

dx

; (Tp + 1) · y(p) = Kx(p); К ( p) !

Кp

;

dt

dt

Tp '1

h( p) !

К

К

e #

t

;

h(t ) !

T

.

Tp '1

T

Для колебательного звена вводим такие понятия, как «коэффици-

ент (декремент) затухания» d и рассмотрим несколько ситуаций: d = 0 – незатухающие колебания;

0 < d B 1 – затухающие колебания;

d > 1 – колебания отсутствуют – апериодическое звено второго порядка.

15

Дифференциальное уравнение имеет вид:

T 2

d 2 y

' 2dt

dy

' y ! Kx; (T

2 p2

' 2dTp '1)

$ y( p) ! Kx( p);

dt 2

dt

1

К ( p) !

К

; h( p) !

К

;

T 2 p2 ' 2dTp '1

p(T 2 p2

' 2dTp #1)

1

1

<1 #e

dt

1

sin(3t ' C)=,

h(t ) ! K

T

$

>

3T

?

@

A

где 3 !

1 #d 2

, α = arcsin(ΩT).

T 2

Для пропорционального звена:

y = Kx; y(p) = Kx(p); K(p) = K; h( p) ! К ; h(t) = K. p

2.3..GBG>>=>?AWX@Q;O>=<;FGI=>?AWXF@<W

O;=<@A=A@SEF=A?=F

Системы автоматического управления в большинстве случаев являются замкнутыми. Однако при их анализе и проектировании ча-

сто предварительно рассматривается разомкнутая цепь звеньев, ко-

торая затем замыкается.

Различают последовательное, параллельное и параллельное с обратной связью соединение звеньев.

Последовательным соединением звеньев называется такое соединение, когда выходная величина предыдущего звена является вход-

ной величиной последующего звена.

x

y

y2

yп

К1

( р)

1

К2 ( р)

К п ( р)

Рис. 2.1. Схема последовательного соединения звеньев

Передаточная функция всей цепи: К Э ( p) ! yn ( p) . x( p)

16

x( p)

Передаточные функции звеньев:

( p) !

y ( p)

( p) !

y2 ( p)

; …; K

( p) !

y

( p)

К

1

; К

2

n

n

,

1

x( p)

y1 ( p)

yn #1 ( p)

где x(p), y1(p), ..., yn(p) изображение по Лапласу соответствующих переменных.

Если перемножить правые и левые части выше приведенных ра-

венств, получим

yn ( p) ! К Э ( p) ! К1 ( p) $K 2 ( p) $!$K n ( p).

Поскольку все переменные y1(p), y2(p), ..., yn–1(p) при перемножении сократятся, то

n

КЭ ( p) ! DК i ( p).

i !1

Параллельным соединением звеньев называют такое соединение, когда на входы всех звеньев подается одна и та же величина, а выход-

ные сигналы суммируются.

К1( р ) y1

x

y2

y2

К2 ( р )

yn

К3 ( р )

Рис. 2.2. Схема параллельного соединения звеньев

Если параллельно соединены n звеньев, то входной сигнал:

n

x = x1 = ...xi = ...= xn, а выходной: y ! Eyi .

i !1

17

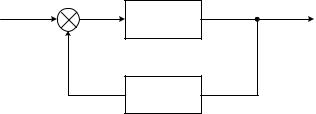
Переходя к изображениям и учитывая, что yi(p) = Ki(p) · xi, полу-

n	n	n
чим y( p) ! EK i ( p) $ xi ( p) ! x( p)EK i ( p) , т. е. K Э ( p) ! EK i ( p),
i !1	i !1	i !1
n
следовательно hЭ (t ) ! Ehi (t ). .

i!1

2.4.)NBGIAW=OFSE@..;>;Y@I=>?AGS,;IB@CGI=>?AGS, D@NMGS@Y=OIMGS;NBGIAW=OFSE@

Обратная связь может быть положительной, если сигнал обратной связи XОС складывается с входным сигналом X (плюс Y суммирующего элемента), или отрицательной, если XОС вычитается из X (ми-

нус Y суммарного элемента).

x	y
К1	( р )

(± )

x oc

К2 ( р )

Рис. 2.3. Схема обратной связи

Схема описывается при отрицательной обратной связи следующими уравнениями: y(p) = K1(p)[x(p) – xOC(p)], xOC(p) = K2(p) · y(p), ис-

		5						К1 ( p)x( p)
			Fy( p) !
								' k1 ( p)K 2 ( p))
			F	(1							.
ключив из уравнений xOC(p), получим: 6								К1 ( p)
			FК ( p) !
			F		(1 ' К1 ( p)K 2 ( p))
		8
При положительной обратной связи:				К ( p) !				К1 ( p)			.
						(1 # k1 ( p)K 2 ( p))
Передаточная функция разомкнутой САР (см. рис. 2.4):
К		( p) !	y( p)	.
	p		Gx( p)

18

19

x( p )

∆ x ( p )

y ( p )

Рис. 2.4. Схема разомкнутой САР

Передаточная функция замкнутой САР (см. рис.2.3):

К ( p) !	К p	( p)
			.

1 ' К p ( p)К OC ( p)

Если в цепь обратной связи включить пропорциональное звено (это звено, коэффициент передачи которого не является функцией от

частоты), то такая обратная связь называется жесткой обратной свя-

зью KOC(p) = K, если KOC(p) = 1, то это единичная обратная связь.

Для единичной обратной связи: К ( p) ! К p ( p) 1 ' К p ( p)

Если раскрыть Kp(p) и записать коэффициент передачи в общем

виде:

y( p)

b

pm ' b

pm #1 'H' b

К ( p) !

!

m

m #1

0

, где c

= a

+ b

.

pn 'C

pn #1 'H'C

x( p)

C

n #1

0

i

i

i

n

Если в цепь обратной связи включить дифференцирующее звено вида: KOC(p) = K · p, то обратная связь будет называться гибкой обратной связью.

Передаточная функция САР по ошибке задающего воздействия

имеет следующий вид: K

( y ) ! Gx( p) !

x( p) # y( p)

!1 # K ( p) .

x

x( p)

x( p)

Для единичной обратной связи:

К p ( p)

1

a pn ' a

pn #1 '!' a

К

( p) !1 #

!

!

n

n #1

0

,

' К

' К

pn 'C

x

1

p

( p) 1

p

( p)

C

n

n #1

pn #1 '!'C

0

где ci = ai + bi .

3.*'!#)#1&$:'/'+#$/"!#"+"9"1'%"*$!+":5($18$(

"!"!#$%'(#)%'#"*$!+),)/$,-0"/)('1"2

3.1.*GOI;IAGSQ=B=<GI;PAGSHJAMC@S. 'RQ>@IJ<A;-HGE;FGSPGOI;IAGSVGBGMI=B@OI@MG, GRQ>@IJ<AGS@HGE;FGSPGOI;IAW=VGBGMI=B@OI@M@

Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т. е. вынужденные синусоидальные колебания звена.

Если на вход звена подается величина x(t) = sinωt, то на выходе в установившемся режиме получим: y(t) = A(ω)sin(ωt + φ), где A(ω) – амплитуда (точнее, усиление амплитуды), а φ(ω) – фаза (точнее, сдвиг по фазе).

Применяется символическая запись синусоидальных колеба-

ний:

x(t) = ejωt; y(t) = A(ω)e j(ωt + φ(t)).

Поставив эти величины в уравнение звена вида

a0yn + a1y n–1 + ... + any = b0x m + a1x m–1 + ...+ amx , получим

(a0(jω)n + a1(jω)n–1 + ... + an) A(ω)ej(ωt + φ(t)) =

= (b0(jω)m + b1(jω)m–1 + ... +bm)ejωt

откуда A(;)e j ( ;t ':(t )) ! b0 ( j;)m ' b1 ( j;)m #1 '!' bm . a0 ( j;)n ' a1 ( j;)n #1 '!' an

Сравнивая это выражение с передаточной функцией звена: K(p)

=y(p)/x(p), получим: A(ω)e jφ(ω) = (K(p))p = jω = K(jω).

Откуда находим: A(ω) = |K(p)| = K(jω); φ(ω) = argK(jω).

K(jω) называется частотной передаточной функцией звена, которая является комплексной функцией от действительной переменной ω.

Выражение A(;)e j ( ;t ':(t )) ! b0 ( j;)m ' b1 ( j;)m #1 '!' bm представля- a0 ( j;)n ' a1 ( j;)n #1 '!' an

ет собой амплитудно-фазовую характеристику звена (АФЧХ). Выражения A(ω) = |K(p)| = K(jω); φ(ω) = argK(jω) называются соответствен-

но амплитудной частотной характеристикой звена (АЧХ) и фазовой

частотной характеристикой звена (ФЧХ).

20